
Пособие ТСиСА
.pdfдства университета на имя ректора; положительное решение вопроса о восстановлении; подготовка индивидуального графика обучения студента для ликвидации разницы в учебных планах; подготовка приказа о восстановлении; утверждение приказа о восстановлении ректором; ликвидация академических задолженностей студентом; получение студенческого билета; получение зачетной книжки.
20. Выполнить построение |
по заданной структуре графическо- |
||||
го представления сетей Петри. |
|
|
|
|
|
S=(P, T, I, O); P={P1, P2, P3, P4, P5, P6} |
T={t1, t2, t3, t4, t5} n=6, |
||||
m=5. Вектор начальной маркировки сети: |
M= (1,2,0). |
I(t1)={P1}; |
|||
O(t1)={P2, P3}; |
(t2)={P3}; O(t2)={P3, |
P5, |
P5}; I(t3)={P2, P3}; |
||
O(t3)={P2, P4}; |
I(t4)={P4, P5, |
P5, P5}; |
O(t4)={P4}; |
I(t5)={P2}; |
|
O(t5)={P6}. |
|
|
|
|
|
21. Выполнить построение |
по заданной структуре графическо- |
||||
го представления сетей Петри. |
|
|
|
|
|
S= (P, T, I, O); P={P1, P2, P3, P4, P5, P6}; T={t1, t2, t3, t4}; n=6, m=4. Вектор начальной маркировки сети: M=(1,0,0,0,0,0). I(t1) = {p6}; O(t1)
= {P1, P2, P3}; I(t2) = {p1, p2}; O(t2) = {p4} I(t3) = {p2, p3, p3, p4}; O(t3) = {P5, P5}; I(t4) = {P5}; O(t4) = {P6}.
22. Выполнить построение по заданной структуре графического представления сетей Петри.
S = (P, T, I, O); P= (P1, P2, P3, P4, P5); T= (t1, t2, t3, t4); n=5, m=4.
Вектор начальной маркировки сети: M= (1,0,0,0,0). I(t1)={P1}; I(t2)={P2}; I(t3)={P3}; I(t4)={P4}; O(t1)={P2}; O(t2)={P3}; O(t3)={P4}; O(t4)={P5}.
23. Выполнить построение по заданной структуре графического представления сетей Петри.
S = (P, T, I, O); P= (P1, P2, P3, P4, P5, P6); T= (t1, t2, t3, t4, t5, t6,); n=6, m=6. Вектор начальной маркировки сети: M= (1,0,0,0,0,0). I(t1)={P1};
I(t2)={P2}; I(t3)={P1}; I(t4)={P3}; I(t5)={P1}; I(t6)={P4}; O(t1)={P2}; O(t2)={P1}; O(t3)={P3}; O(t4)={P1}; O(t5)={P4}; O(t1)={P2}.
110
Контрольные вопросы
1.Перечислите основные элементы сети Петри.
2.Какая сеть называется ординарной?
3. Укажите основные области применения сетей Петри.
4. Что понимается под маркировкой и маркером?
5.Что понимается под емкостью позиций, и при каких условиях количество маркеров внутри позиции отображается числом?
6.В чем заключается срабатывание перехода сети Петри?
7. Какие позиции называются конфликтными?
8. Опишите коротко процесс функционирования сети Петри.
9.Почему сеть Петри представляет собой конечный, ассиметричный, двудольный, направленный мультиграф?
10.Что порождает новую маркировку сети Петри?
11.Какие программы визуального моделирования позволяют вводить описание моделируемой системы преимущественно в графической форме?
12.Какие существуют способы задания сети Петри?
13.Какое представление теории сетей Петри является наиболее наглядным?
14.Для моделирования каких систем применяются Сети Петри?
111
Заключение
Сеть Петри можно представить как поведенческую модель, которая отображает процессы, обеспечивающие функционирование системы в условиях ограниченности ресурсов и при наличии внешних положительных и отрицательных воздействий, которые могут способствовать, или затруднять правильное функционирование системы. С помощью сетей Петри возможно многократно исследовать как систему, так и ее внутренние процессы, определяя оптимальные решения, выполняя построение прогнозов, накапливая при этом выходные данные, которые, в последствии, могут быть перенесены на реальную систему.
При этом сети Петри широко применяются для моделирования сложных систем, например, производственных предприятий, нефтегазовых комплексов, вычислительных систем и сетей, программных комплексов и многих других. Кроме того, с помощью сетей Петри можно построить модель практически любой слабо формализуемой и многокомпонентной системы, для которой затруднено применение строгих методов.
Формальное построение сети можно разделить на несколько этапов:
–объявление множеств (типов данных) и переменных;
–моделирование и запуск сети;
–анализ результатов выполнения.
Моделирование в сетях Петри осуществляется на событийном уровне:
–определяются, действия, которые происходят в системе;
–состояния, которые предшествовали данным действиям;
–состояния, которые примет система после выполнения данных действий.
Позиции обозначаются текстовым названием, множеством и маркерами, переходы – текстовым названием и условием срабатывания. Присвоение маркеров позициям сети Петри называют маркировкой. Динамика сетей Петри связана с механизмом изменения маркировок позиций и соглашениями о правилах срабатывания переходов.
Неформально работу сети можно представить как совокупность локальных действий, называемых «срабатываниями переходов»
112
и приводящих к изменению маркировки, т.е. локальному изменению условий в системе. Срабатывание перехода представляется как неделимое действие, изменяющее разметку входных и выходных позиций. Таким образом, срабатывание перехода состоит в изъятии маркеров из каждой входной позиции и помещении их в каждую выходную позицию до тех пор, пока не будет получена тупиковая, конечная (или завершающая) маркировка. Причем количество маркеров, изымаемых из конкретной позиции, или помещаемых в конкретную позицию, равно количеству дуг, соединяющих срабатывающий переход с данной конкретной позицией.
113
ГЛАВА 4. АНАЛИЗ СЕТЕЙ ПЕТРИ
В данном разделе рассматривается анализ синтаксиса и динамики функционирования модели сети Петри. Приводятся основные свойства сетей Петри: ограниченность, безопасность, сохраняемость, живость, устойчивость, терминальность и достижимость. Описывается алгоритм построения дерева покрывающих маркировок для заданных сетей Петри, а также методика исследования основных свойств сетей с помощью дерева покрывающих маркировок. Предлагаются практические примеры моделей систем для анализа и определения основных свойств сетей Петри в рамках конкретной предметной области.
4.1.Общие теоретические сведения
Спомощью сетей Петри можно моделировать широкий класс систем, представляя необходимым образом взаимодействие различных процессов, которые обеспечивают функционирование системы. Моделирование системы на основе сетей Петри предполагает прове-
дение тщательного анализа, который должен привести не только к уверенности в том, что модель соответствует системе и работает надлежащим образом, но и к глубокому пониманию поведения моделируемой системы. Таким образом, анализ сети Петри включает в себя предварительный этап, на котором специалист определяет, является ли построенная модель системы оптимальной, работает ли модель должным образом, свободна ли система от ошибок или есть необходимость их устранения, а также принимает решение к модификации модели.
Анализ синтаксиса модели и пошаговое моделирование, используются, чтобы определить корректность распределения и путь перемещения маркеров (ресурсов) в модели системы.
Анализ динамики функционирования системы и характера множеств возможных последовательностей срабатываний переходов используется для решения задач, например, для определения выполняет ли сети Петри положенный в ее основу алгоритм функционирования системы.
Таким образом, необходимо рассмотреть методы анализа и свойства сетей Петри.
114
4.2. Свойства сетей Петри
Ограниченность (K-ограниченность) – сеть Петри является ограниченной, если число маркеров в любой из ее позиций не может превысить некоторого фиксированного числа (K). Ограниченность сети означает, что число ее состояний конечно. Неограниченный рост числа маркеров в какой-либо позиции свидетельствует о нарушениях ограниченности и об опасности неограниченного роста длин очередей ресурсов.
Число К называют также емкостью позиции. Сеть Петри ограничена, если ограничены все ее позиции. При этом если известны емкости всех позиций, и наибольшая из них Kmax, то сеть называют Kmax
– ограниченной.
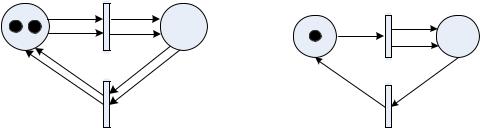
Практическое значение свойства ограниченности, в частности, состоит в следующем. При проектировании информационных систем определение емкости позиции позволяет обоснованно выбирать емкость накопителя [10]. Например, сеть на рис. 48, а является ограниченной – при любом срабатывании сети количество маркеров в любой позиции не превысит двух, а сеть на рис. 48, б не является ограниченной – количество маркеров в любой позиции может увеличиваться бесконечно.
P1 |
t1 |
P2 |
P1 |
t1 |
P2 |
|
|
|
|||
|
t2 |
|
|
t2 |
|
|
|
|
|
|
а б
Рис. 48. Свойства сети Петри: а – ограниченная (К=2) сеть Петри; б – неограниченная сеть Петри (К= )
Безопасность – частный случай ограниченности. Свойство сети, определяемое условием K=1 (число маркеров в любой позиции не превышает одного) [10]. В безопасных сетях каждый переход сети имеет ровно одну входную и одну выходную дуги и при своем срабатывании изымает один маркер из входной позиции и добавляет его в выходную.
115
Таким образом, позиция безопасна, если ее емкость |
(количест- |
во маркеров в ней) равно нулю или одному. |
Сеть Пет- |
ри безопасна, если безопасны все позиции сети. |
|
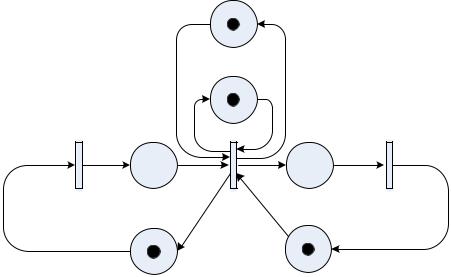
На рис. 49 представлена модель процесса выдачи тем курсовых |
|
работ студенческой группе. Данная сеть Петри является безопасной, т.к. число маркеров внутри каждой позиции не превышает одного.
P1
P5
t1 |
P4 |
P6 |
t3 |
P3 |
t2 |
P2 |
|
Рис. 49. Пример безопасной сети Петри
Содержательный смысл позиций: P1 – преподаватель; P2 – студент; P3 – выбранная тема курсовой работы студентом и обоснование ее целесообразности; P4 – согласование выбранной темы с преподавателем; P5 – методические указания для выполнения курсовой работы; P6 – формирование протокола выдачи тем курсовых работ студенческой группе.
Содержательный смысл переходов: t1 – проверка темы курсовой работы преподавателем t2 – закрепление выбранной темы курсовой работы за студентом; t3 – проверка истечения установленного срока для выдачи тем курсовой работы.
Сохраняемость (консервативность) – свойство сети, характе-
ризующее невозможность возникновения или уничтожения ресурсов в моделируемом объекте, т.е. общее число маркеров в сети должно остаться постоянным. Свойство сохранения, в частности, может гарантировать для системы, что количество находящихся подсистем, элементов не изменяется.
116
Строгая сохраняемость – частный случай сохраняемости, свойство сети, из которого следует, что число входов в каждый переход должно равняться числу выходов из перехода.
Основная цель рассмотрения свойств консервативности и строгой сохраняемости – определение ресурсов, которые исчезают или возникают в процессе функционирования системы.
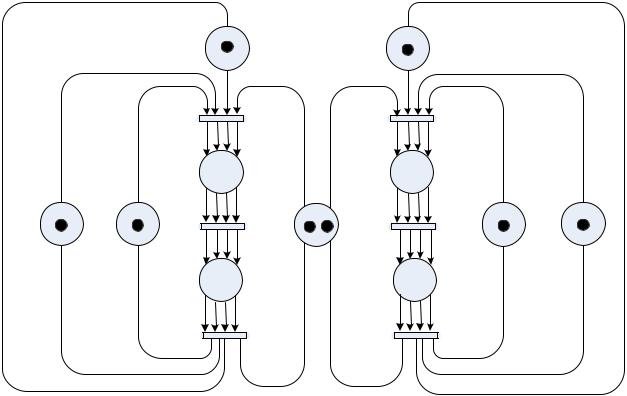
Рассмотрим пример свойства сохраняемости на модели процесса посещения лабораторных работ студенческой группой (рис. 50). Количество маркеров в позиции P1 и P2 соответствует количеству преподавателей, которые проводят лабораторную работу (в рассматриваемой лабораторную работу организует один преподаватель).
P1 |
P2 |
|
t1 |
|
t2 |
|
|
P3 |
|
P4 |
|
P7 |
P5 |
P5 |
P6 |
P8 |
|
||||
|
t3 |
|
t4 |
|
|
P9 |
|
P10 |
|
|
|
|
|
Рис. 50. Пример строго сохраняемой сети Петри
Наличие маркера в позиции P3 и P4 соответствует состоянию «посещение лабораторной работы» (должно быть не более двух маркеров, так как преподаватель не может одновременно принимать лабораторную работу у двух подгрупп, а одна подгруппа одновременно присутствовать на двух лабораторных работах). Количество маркеров в позиции P5 соответствует числу подгрупп в студенческой группе
117
(в рассматриваемой системе две подгруппы). Позиции P6 и P7 определяют наличие свободных специально оборудованных помещениях для выполнения лабораторной работы. Позиции P6 и P7 соответствуют наличию методических указаний для выполнения лабораторной работы.
Переходы t1 и t2 выполняют проверку получения задания и проверку наличия специально оборудованных помещений для выполнения лабораторной работы, t3 и t4 выполняют проверку результатов выполнения лабораторной работы преподавателем.
Живость – свойство, которое определяется возможностью срабатывания любого перехода при функционировании моделируемой системы. Отсутствие живости означает либо избыточность аппаратуры в системе, наличие неисполняемых функций в программе, либо свидетельствует о возможности зацикливаний, тупиков и блокировок. Зацикливание – наличие таких циклов, из которых невозможно вернуться в начальное состояние системы. При организации параллельного выполнения нескольких вычислительных процессов одной из главных функций операционной системы является решение сложной задачи корректного распределения ресурсов между выполняющимися процессами и обеспечение последних средствами взаимной синхронизации и обмена данными. При параллельном исполнении процессов могут возникать тупиковые ситуации, когда два или более процесса блокируют друг друга, вынуждая ожидать наступления события, связанного с освобождением ресурса. Самым простым является случай, когда каждый из двух процессов ожидает ресурс, занятый другим процессом. Из-за такого ожидания ни один из процессов не может продолжить свое выполнение и освободить ресурс, необходимый другому процессу. Данная ситуация называется тупиком.
Итак, тупиковая маркировка – это маркировка, при которой не существует ни одного перехода, который не может сработать при данной маркировке, по крайней мере, один раз.
Рассмотрим уровни живости (активности) переходов.
Уровень 0: Переход обладает активностью уровня 0, если он никогда не может сработать. Переход с нулевым уровнем активности называют пассивным.
118
Уровень 1: Переход обладает активностью уровня 1, если существует достижимое из начального состояния, в котором он разрешен (активен) только один раз.
Уровень 2: Переход обладает активностью уровня 2, если для всякого целого n существует последовательность запусков сети Петри, в которой данный переход присутствует, по крайней мере, n раз.
Уровень 3: Переход обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой присутствует неограниченное число раз.
Уровень 4: Переход обладает активностью уровня 4, если для любого достижимого состояния существует последовательность срабатываний других переходов, приводящая в такое состояние, в котором рассматриваемый переход будет разрешен (активен) [11].
Анализ модели на свойство живучести позволяет выявить невозможные состояния в моделируемой системе (например, неисполняемые ветви в программе). Доказав, что сеть является живой, можно гарантировать, что в соответствующей системе выполнимы все элементарные действия процессов.
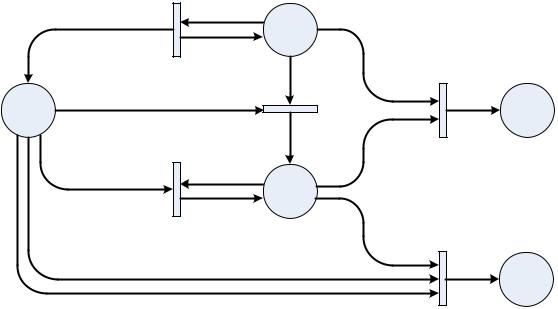
Рассмотрим уровни активности переходов, проиллюстрируем сетью на рис. 51
|
t3 |
P2 |
|
|
|
|
|
P4 |
|
t1 |
P1 |
|
|
|
|
|
|
t2 |
|
|
t4 |
P3 |
|
|
|
|
t5 P5
Рис. 51. Уровни активности переходов
119
