
ТОЭ РГР 3Схема
.docx
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра теоретических основ электротехники
Контрольная работа №3
Расчет переходных процессов
в линейных цепях
Шифр 100610 вариант №10
Выполнил: студент заочного отделения
Проверил: к.т.н. доцент
Преподаватель: Лукманов В.С.
Уфа
Вариант № 10
Схема №3
R1 = 26 Ом R2 = 76 Ом R3 = 91 Ом R4 = 66 Ом L = 93 мГн C = 66 мкФ E = 304 В
Найти
 -?
-?

Рис. 1 Исходная схема
Задание:
-
Рассчитать закон изменения тока (напряжения) в функции времени классическим методом.
-
Рассчитать закон изменения тока (напряжения) в функции времени операторным методом.
-
На основании полученного аналитического выражения построить график изменения искомой величины в зависимости от времени на интервале от
 до
до
 .
.
-
Классический метод определения тока
Искомый
ток
 ищем
в виде суммы установившегося и свободного
токов:
ищем
в виде суммы установившегося и свободного
токов:
 .
.
Цепь до коммутации:
![]()

Рис. 2 Цепь до коммутации

Цепь после коммутации:
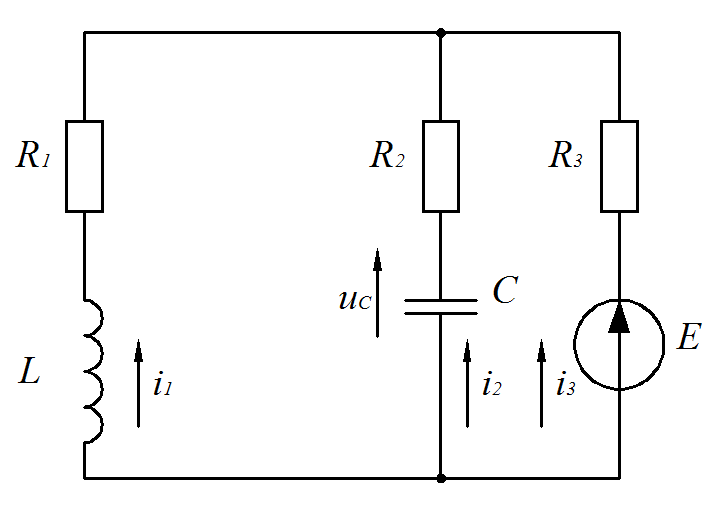
Рис. 3 Цепь после коммутации
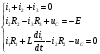
Установившийся режим при t = ∞:

Рис. 4 Цепь в установившимся режиме при t = ∞

Найдем
характеристическое сопротивление цепи


Рис.
5 Схема для определения характеристического
сопротивления цепи
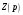
Составим
выражение для определения характеристического
сопротивления цепи
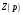 :
:
 Найдем
корни характеристического уравнения
для этого приравняем
Найдем
корни характеристического уравнения
для этого приравняем
 к нулю:
к нулю:

Т.к. корни уравнения вещественные числа, то выражение свободного тока примет вид:

Чтобы
найти коэффициенты
 воспользуемся
начальными условиями.
воспользуемся
начальными условиями.
Ток в индуктивных катушках и напряжения на конденсаторах в момент коммутации
не изменяются скачками (независимые начальные условия):

Уравнения Кирхгофа для момента коммутации:

Откуда находим зависимые начальные условия:


Выражения для искомого тока:

Для определения постоянных интегрирования решим систему из выражений искомого тока в момент коммутации и его производной в момент коммутации:

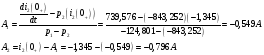
Таким
образом,
получаем
выражение тока
 для
любого момента времени
для
любого момента времени
 :
:

-
Операторный метод определения тока
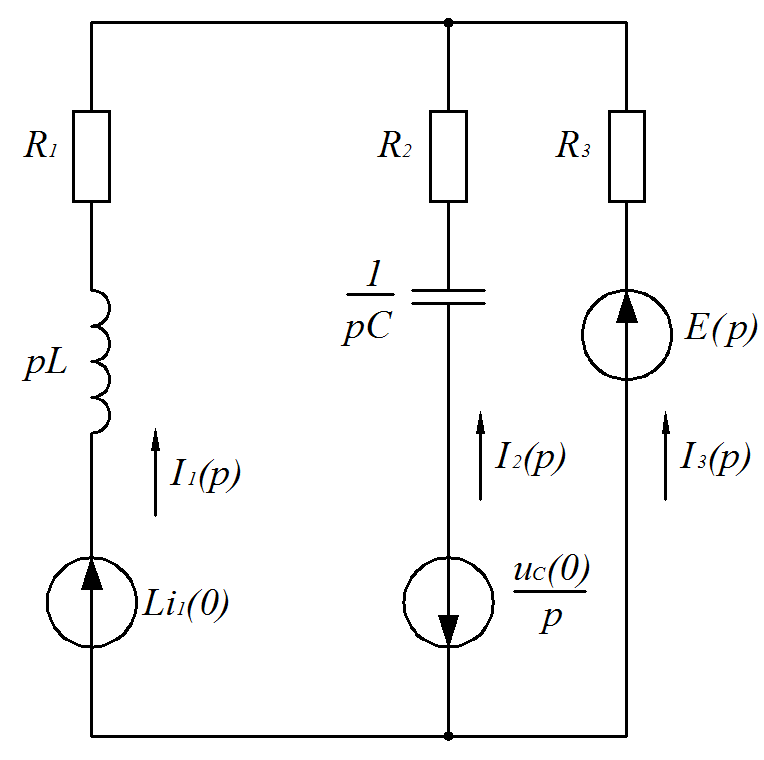
Рис. 6 Схема для операторного метода
Независимые начальные условия:





Из третьего уравнения полученной системы уравнений выделим выражение изображения для искомого тока:

Т.к.
изображение искомой величины – отношение
двух полиномов ,
то для нахождения оригинала по найденному
изображению при помощи обратного
преобразования Лапласа используем
теорему разложения:
,
то для нахождения оригинала по найденному
изображению при помощи обратного
преобразования Лапласа используем
теорему разложения:
Т.к.
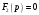 при
при
 ,
то
,
то



 Подставляя
полученные значения в исходную формулу
для нахождения оригинала, получим
искомое значение тока:
Подставляя
полученные значения в исходную формулу
для нахождения оригинала, получим
искомое значение тока:
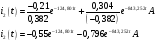
-
График зависимости тока
 от
времени
от
времени

Рис.
7 График функции тока

Постоянная
времени

Время
переходного процесса

Проверка ответов:
"A1": -0,549
"A2": -0,796
"DT1": -2347,636
"DT2": 739,576
"DT3": 1608,059
"DUC": -17933,333
"I10": -2,972
"I1Y": -6,071
"I20": -1,345
"I30": 4,319
"I3Y": 6,071
"P1": -124,801
"P2": -843,252
"UC0": -68,356
"UCY": -139,633
"Фи": 0
