
Mnozhestva2
.pdfМинистерство образования и науки Российской Федерации Федеральное агентство по образованию
Ярославский государственный университет им. П.Г. Демидова Кафедра теоретической информатики
В.С. Рублев
Множества
(бинарные отношения множеств, мощность множеств) (индивидуальная работа № 10а по дисциплине
¾Дискретная математика¿)
Методические указания
Ярославль 2015

Содержание
1 Отношения множеств |
2 |
1.1Прямое произведение множеств . . . . . . . . . . . . . . . 2
1.2Определение отношения множеств . . . . . . . . . . . . . 4
1.3Взаимно-однозначное соответствие . . . . . . . . . . . . . 4
1.4Бинарные отношения эквивалентности и порядка . . . . 8
|
|
1.4.1 |
Отношение эквивалентности . . . . . . . . . . . . |
9 |
|
|
1.4.2 |
Отношение порядка . . . . . . . . . . . . . . . . . |
12 |
2 |
Мощность множеств |
19 |
||
|
2.1 |
Счетные множества . . . . . . . . . . . . . . . . . . . . . |
20 |
|
|
2.2 |
Несчетные множества . . . . . . . . . . . . . . . . . . . . |
22 |
|
|
2.3 |
Примеры установления мощности множества с обоснова- |
|
|
|
|
нием . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
23 |
|
3 |
Цель работы и общее задание |
26 |
||
4 |
Варианты индивидуального задания 10а |
28 |
||
1Отношения множеств
1.1Прямое произведение множеств
Пусть заданы множества A1; : : : ; An. Кортежем < a1 : : : ; an >1 называется последовательность элементов этих множеств, где ai 2 Ai (i 2 1; n), а прямым произведением множеств называется множество кортежей
n |
|
|
|
|
Yi |
|
|
|
|
A1 £ A2 £ ¢ ¢ ¢ £ An = Ai = f< a1 |
: : : ; an > j ai 2 Ai |
(i 2 |
1; n |
)g: |
=1 |
|
|
|
|
Прямое произведение k одинаковых множеств A обозначается Ak. В этом случае в кортеже все компоненты имеют одну природу, и такой кортеж называется вектором. Например, a = (a1; : : : ; ak) 2 Ak.
Рассмотрим примеры.
1 Кортеж отличается от вектора тем, что его элементы могут принадлежать разным множествам.
2

1. A = fa; bg, B={c, d, e}. Тогда
A £ B = f< a; c >; < a; d >; < a; e >; < b; c >; < b; d >; < b; e >g:
2.Множество k-значных целых неотрицательных чисел есть подмножество прямого произведения Ck, где C = f0; 1; : : : ; 9g – множество цифр.
3.Слова есть подмножество объединений прямых произведений
[1 Yk
A = A¤; 2
k=1 1
где A – алфавит (множество букв языка).
Проекцией кортежа прямого произведения на i-ю ось называется i- я компонента кортежа. Проекцией кортежа v =< a1; : : : ; an > на оси
i1; : : : ; ik называют кортеж < ai1; : : : ; aik >. Проекция прямого произведения на i-ю ось обозначается Пр1A1 £ ¢ ¢ ¢ £ An = Ai.
Теорема о количестве элементов прямого произведения множеств.
Количество элементов прямого произведения конечного числа конечных множеств равна произведению количеств элементов каждого из множеств
|
j Aij = |
jAij |
. |
i=1 |
i=1 |
|
|
Доказательство проведем с помощью метода математической индукции.
Основание индукции. При n = 1 утверждение очевидно. При n = 2
A1 £ A2 = |
jjA=11jf< aj1; al2 > j l 2 |
|
|
|
|||||||||||||||||||||||||||||||
1; jA2jg. Так как количество элементов |
|||||||||||||||||||||||||||||||||||
множестваS |
|
< aj1 |
; al2 > |
|
l |
|
|
|
|
|
|
|
= A2 |
|
не зависит от выбора эле- |
||||||||||||||||||||
|
j |
2 |
1; |
A2 |
jgj |
j |
|||||||||||||||||||||||||||||
|
|
|
jf |
|
|
|
|
|
|
|
|
j |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
j |
|
|
|
|
|
|
|
|
|
|
|
(j 2 1; jA1j), то jA1 |
£ A2j = |
|
|
A1jjA2j = jA1j ¢ jA2j, что и |
||||||||||||||||||||||||||||||
мента aj |
j=1 |
||||||||||||||||||||||||||||||||||
требовалось показать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k+1 |
|||||||||||||
Шаг индукции. Пусть утверждение верно при любом n · k. j |
A |
i=1 Aij = |
|||||||||||||||||||||||||||||||||
|
k |
|
Ak+1 |
|
= |
|
|
k |
|
|
|
Ak+1 |
|
= |
|
|
k |
|
Ai |
Ak+1 |
|
= |
|
k+1 |
|
, что и |
|||||||||
j Q |
i=1 Ai |
¢ |
j |
j Q |
i=1 |
j ¢ j |
j |
Q |
i=1 |
j |
j |
Q |
i=1 |
Qi |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j ¢ j |
|
|
j j |
|
||||||||||||||
доказывает шаг индукции. Доказательство закончено.
2 A¤ – обозначение замыкания множества
3
1.2Определение отношения множеств
Отношением множеств называется подмножество прямого произведения этих множеств.
Число множеств, входящих в различные отношения может быть разным. При двух множествах входящих в отношение оно называется бинарным отношением, при трех – тернарным, и т.д.
Наиболее употребительны в математике бинарные отношения. Пусть R µ A £ B. Тогда отношение определяется некоторым набором двоек < a; b >2 R (a 2 A; b 2 B). Часто такое отношение различных множеств A и B называется соответствием.
Пр1R – область определения R, а Пр2R называется областью значений R.
Если Пр1R = A, то соответствие R всюду определено. Если Пр2R = B, то соответствие R сюръективно.
Обратное соответствие определяется следующим образом:
R¡1 = f< b; a > j < a; b >2 Rg.
Если < a; b >2 R, то b – образ a, а a – прообраз b.
Для множества X образ X есть R(X) = fyj 9x 2 X :< x; y >2 Rg, а для Y прообраз Y есть R¡1(X) = fxj 9y 2 Y :< y; x >2 R¡1g.
Из определений следует, что R(Пр1R) =Пр2R и R¡1(Пр2R) =Пр1R. Соответствие R функционально (однозначно), если
8a 2Пр1R : jfbj < a; b >2 Rgj = 1.
Обратное соответствие R¡1 функционально (однозначно), если
8b 2Пр2R : jfaj < a; b >2 Rgj = 1.
1.3Взаимно-однозначное соответствие
Соответствие называется взаимно-однозначным, если оно всюду определено, функционально и обратное соответствие также всюду определено и функционально. Таким образом, для проверки того, что R µ A £ B является взаимно-однозначным соответствием требуется установить, что выполняются следующие условия:
1.Соответствие R(a) = b всюду определено на A, т. е.
8a 2 A 9b 2 B : R(a) = b.
4
2.Соответствие R(a) = b является функциональным (каждому аргументу ставится в соответствие точно 1 значение), т. е.
jfbj < a; b >2 Rgj = 1.
3.Обратное соответствие R¡1(b) = a всюду определено на B (соответствие R сюръективно), т. е. 8b 2 B 9a 2 A : R¡1(b) = a или
R(a) = b.
4.Обратное соответствие R¡1(b) = a является функциональным (каждому аргументу ставится в соответствие точно 1 значение), т. е. jfaj < b; a >2 R¡1gj = 1 или jfaj < a; b >2 Rgj = 1.
Взаимно-однозначное соответствие часто также называют биекцией. Рассмотрим примеры соответствий.
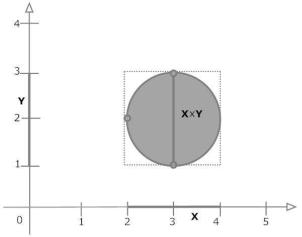
1.R – круг (x ¡ 3)2 + (y ¡ 2)2 · 1 (рис.1). Для x = 2 y = R(2) = 2 является единственным значением, но для x = 3 множество fy = R(3)j(3; y) 2 Rg представляет отрезок fyj y 2 [1; 3]g, а потому соответствие не функционально.
Рис. 1
5

Рис. 2
2.R – дуга f(x; y)j (x ¡ 3)2 + (y ¡ 2)2 = 1; y ¸ 2g (рис.2). Соответствие R определено на отрезке x 2 [2; 4] и является функцио-
нальным, так как 8x значение y определяется однозначно функ- p
цией y = R(x) = 1 ¡ (x ¡ 3)2 + 2, но обратное соответствие p
x = R¡1(y) = § 1 ¡ (y ¡ 2)2 + 3 является неоднозначным, т. е. не является функциональным.
3. R – дуга f(x; y)j (x ¡ 3)2 + (y ¡ 2)2 = 1; y ¸ 2; x ¸ 3g (рис.3). Соответствие R определено на отрезке X = [3; 4], имеет область
значений Y = [2; 3] и является функциональным y = R(x) = p
1 ¡ (x ¡ 3)2 + 2. Также является функциональным обратное со- p
ответствие x = R¡1(y) = 1 ¡ (y ¡ 2)2 + 3. Таким образом, соответствие R является взаимно-однозначным для произведения множеств X £ Y .
4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
X xY |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
X |
4 |
5 |
|
6

Рис. 3
4. Множество позиций P OZ на шахматной доске
D = f< x; n > j x 2 a; h; n 2 1; 8g с множеством фигур
F IG = fKrw; F w; Slw; Slw; Knw; Knw; Lw; Lw; P w; P w; P w; P w; P w; P w; P w; P w; Krb; F b; Slb; Sb; Knb; Knb; Lb; Lb; P b; P b; P b; P b; P b; P b; P b; P bg является соответствием
P OZ µ F £ D0 между подмножеством F µ F IG оставшихся фигур и подмножеством D0 µ D клеток доски, на которых стоят эти фигуры. Например, p = f< Krw; < a; 3 >>; < Lw < b; 8 >>; < Krw; < h; 4 >>; < P w < b; 6 >>; < Kn; < d; 7 >>g. Соответствие P OZ является взаимно-однозначным, так как каждая фигура из подмножества F занимает ровно 1 позицию (функция соответствия однозначна на подмножестве оставшихся фигур) и каждая клетка из D0 может быть занята не более, чем одной фигурой из F IG (функция обратного соответствия однозначна на множестве занятых фигурами клеток доски).
5.Англо-русский словарь S µ A £ R осуществляет соответствие между некоторым подмножеством A английских слов и подмножеством R русских слов. Однако, и прямое и обратное соответствие не являются однозначными: образ английского слова может состоять из нескольких русских слов, а прообраз русского слова может иметь несколько английских слов.
Написание фразы взаимно-однозначное соответствие можно сокращать как 1-1с.
Теорема о взаимно-однозначном соответствии.
Между конечными множествами A и B можно установить взаимнооднозначное соответствие тогда и только тогда, когда количество элементов этих множеств одинаково jAj = jBj.
Доказательство.
Достаточность. Пусть jAj = jBj = n. Перенумеруем все элементы
A = fa1; : : : ; ang и B = fb1; : : : ; bng. Построим функцию соответствия R(ai) = bi (i 2 1; n) и функцию обратного соответствия R¡1(bi) = ai (i 2 1; n). Эти функции отвечают всем вышеперечисленным услови-
ям 1-1с. Поэтому нами установлено 1-1с.
7
Необходимость. Пусть существует 1-1с R µ A £ B. Доказательство проведем от противного. Если jAj > jBj, то в A найдутся 2 элемента с одним образом в B, что противоречит 1-1с R. Если же jBj > jAj, то в B найдутся 2 элемента с одним прообразом в A, что опять противоречит 1-1с R. Полученные противоречия завершают доказательство необходимости и всей теоремы.
Теорема о 1-1с позволяет в некоторых задачах комбинаторики обосновать правильность нахождения количества элементов некоторого множества. Для этого устанавливается 1-1с с некоторым другим множеством, число элементов которого может быть подсчитано или уже известно. Установление 1-1с требует определения функций прямого и обратного соответствия. Такое определение каждой функции должно выражать правило, которое определяет значение функции по ее аргументу. Это правило может быть задано либо с помощью формулы, либо словесным образом, либо с помощью таблицы соответствия, либо при помощи алгоритма, вычисляющего по аргументу значение функции. Но в любом случае это должно быть правило, точно и однозначно задающее значение функции по ее аргументу.
Помимо обоснования всюду определенности этих функций необходимо также показать их взаимную обратность Пусть, например, имеются множества A и B и для установления 1-1с определены функция f(a) = b для любого аргумента a 2 A со значением b 2 B, а также функция f¡1(b) = a для любого аргумента b 2 B со значением a 2 A. Хотя функции f и f¡1, осуществляющие соответствие всюду определены (на A и B соответственно), но соответствие f¡1 может не быть обратным для соответствия f, а потому их взаимную обратность нужно обосновать установлением свойств: 8a 2 A : f¡1(f(a)) = a и 8b 2 b : f(f¡1(b)) = b. Этим 1-1с между A и B будет установлено.
1.4Бинарные отношения эквивалентности и порядка
Рассмотрим бинарные отношения множества с самим собой R µ A £ A. Для каждого из таких отношений могут быть выполнены или не выполнены некоторые из следующих свойств:
1. Рефлексивность. 8a 2 A : (a; a) 2 R.
8
2.Антирефлексивность. 8a 2 A : (a; a) 2= R.
3.Симметричность. 8a; b 2 A : (a; b) 2 R ! (b; a) 2 R.
4.Антисимметричность. 8a; b 2 A : (a; b) 2 R ! (b; a) 2= R.
5.Транзитивность. 8a; b; c 2 A : (a; b) 2 R ^(b; c) 2 A ! (b; a) 2 R.
6.Линейность. 8a; b 2 A; a 6= b : (a; b) 2 R _ (b; a) 2 R.
1.4.1Отношение эквивалентности
Отношением эквивалентности называется такое отношение, для которого выполняются свойства 1, 3, 5 (рефлексивности, симметричности и транзитивности).
Тривиальными примерами такого отношения являются отношения равенства чисел, равенства множеств. Принято в качестве обозначения отношения эквивалентности применять знак ` ´0.
Рассмотрим нетривиальный пример для множества N натуральных чисел: a = b mod n (2 числа a 2 N и b 2 N эквивалентны, если они имеют один и тот же остаток при делении на n 2 N). Так при n = 3 эквивалентными числами являются 1, 4, 7,. . . , или 2, 5, 8,. . . , или 3, 6, 9,. . . . Нетрудно видеть, что множество N разбивается этим отношением на 3 непересекающиеся последовательности эквивалентности.
В общем случае вводится понятие класса эквивалентности, как подмножества эквивалентных элементов множества A. Оно может быть определено по любому представителю класса эквивалентности: [a] ´ fb 2 Aj b ´ ag. Нетрудно видеть, что a ´ b влечет [a] ´ [b] и что a 6´b влечет [a] \ [b] = ;. Таким образом, введение отношения эквивалентности разбивает множество на непересекающиеся классы эквивалентности, независимые от представителя. Если образовать множество, выбрав в каждом классе по представителю, то такое множество называется фактор-множеством: FA = fa 2 Aj a; b 2 FA ! [a] 6= [b]g.
9
|
|
y |
|
y |
|
|
[a] |
|
|
|
|
[b] |
|
|
|
|
|
[c] |
F2 ={(0,y)} |
|
|
|
|
a |
|
|
|
|
[a] |
a |
b |
c |
|
|
|
|
F1 ={(x,0)} |
x |
x |
|
|
|
|
b |
|
|
|
|
[b] |
|
|
|
|
c |
|
|
|
|
[c] |
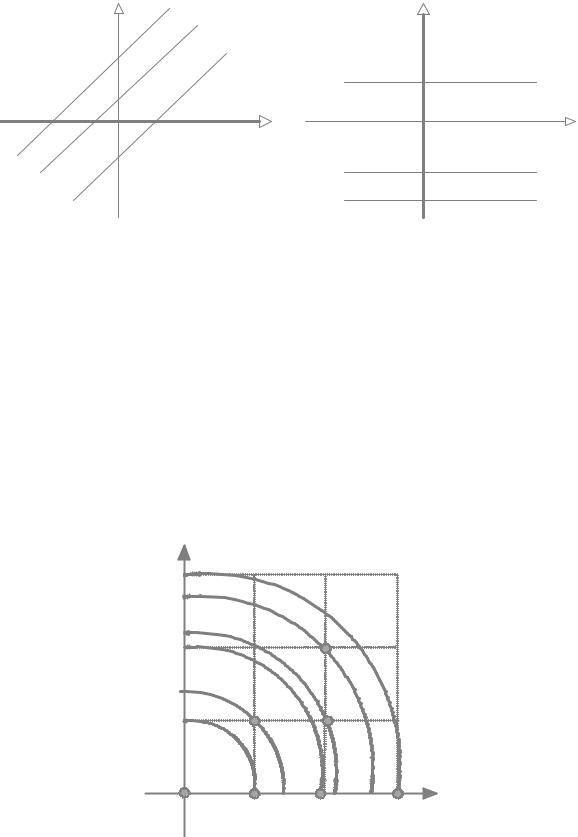
Рис. 4 Приведем примеры фактор множества.
Пример 1.
Рассмотрим вещественную плоскость A = f(x; y)j x; y 2 (¡1; 1)g. Возьмем 2 различных вещественных числа a; b и определим следующее отношение эквивалентности (x1; y1)R(x2; y2) : ax1 +by1 = ax2 +by2. Тогда в качестве фактор-множества при ненулевых значениях a; b можно взять f(x; 0)j x 2 (¡1; 1)g либо f(0; y)j y 2 (¡1; 1)g, а при одном нулевом значении одного из параметров a; b можно взять одно из этих множеств, соответствующее ненулевому параметру. На рис.4 представ-
лены оба эти случая: F1 = f(x; 0)j x 2 Rg и F2 = f(0; y)j y 2 Rg. Пример 2.
3 |
c=9 |
|
|
|
|
|
|
|
c=5 |
|
|
2 |
|
c=8 |
|
|
|
|
|
|
c=2 |
|
|
1 |
|
c=4 |
|
|
|
|
|
|
c=1 |
|
|
|
c=0 |
|
|
0 |
1 |
2 |
3 |
|
|
10 |
|
