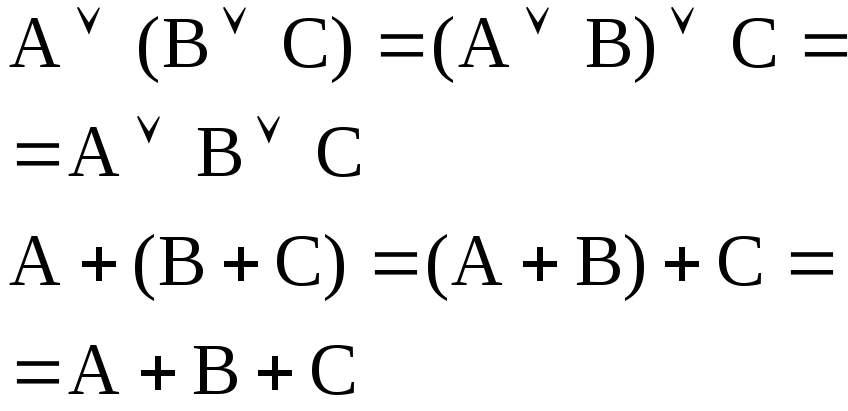2.2. Булева алгебра

В данном разделе излагаются основы булевой алгебры и приво­дятся примеры использования соответствующего математического. аппарата при описании функций и принципов работы комбинаци­онных логических схем. Комбинационной логической схемой назы­вается цифровая схема, в которой выходные сигналы в любой мо­мент времени определяются только теми сигналами, которые по­ступают на вход схемы в тот же момент времени. Очевидно, что все описанные выше схемы являются комбинационными.

Основные теоремы

Как и другие разделы математики, булева алгебра основывается на ряде постулатов, в частности на тех, которые были выдвинуты Хантингтоном в 1904 г. Их следствием являются следующие соотношения для логических переменных, принимающих значения О и 1:

	(2.8а)		(2.8б)
	(2.9а)		(2.9б)
	(2.10а)		(2.10б)
	(2.11а)		(2.11б)

Равенства (2.8а)—(2.10а) соответствуют операции И для двух переменных согласно таблице истинности 2.1; равенства (2.8б)— (2.10б) соответствуют операции ИЛИ (табл. 2.2), а равенства (2.11)—операции НЕ (табл. 2.3). При сравнении выражений (2.8а)—(2.11а) и (2.86)—(2.116) можно заметить, что булевы функции обладают свойством двойственности. Действительно, если в приведенных равенствах заменить 0 на 1, 1 на 0, а затем зна­ки Ù на Ú, то выражения (2.8а)–(2.11а) трансформируются в выражения (2.86)—(2.116). Для большей наглядности соответ­ствующие равенства расположены попарно.

Приведенные равенства справедливы также для булевых пере­менных А, В и С. Важные свойства этих логических переменных иллюстрируются следующими попарно объединенными равенст­вами:

	(2.12а)						(2.12б)
	(2.13а)						(2.13б)
	(2.14а)						(2.14б)
	(2.15а)						(2.15б)
Выражения (2.12)-(2.15) – закон идемпотентности.
		(2.16)				закон двойного отрицания
	(2.17а)						(2.17б)
			(2.18а)					(2.18б)
				(2.19а)				(2.19б)
	(2.20а)						(2.20б)

Равенства (2.12) — (2.16) характеризуют свойства операций И, ИЛИ и дополнения для логической переменной А, а равенства (2.17)—(2.20) выражают соответственно переместительный (коммутативности), соче­тательный (ассоциативности), распределительный (дистрибутивности) законы и закон поглощения. Любое из равенств (2.12)—(2.20) можно реализовать при помощи схем И, ИЛИ, НЕ, описанных в предыдущем разделе. Рассмотрим в качестве примера двойное дополнение (2.16); это равенство можно реализовать при помощи двух инверторов (рис. 2.9.).

Рис. 2.9. Логическая схема двойного дополнения.

На рис. 2.10 приведены две схемы для выражения (2.19б), характеризующего распределительный закон. Эти схемы эквивалентны, но одна из них состоит из двух, а другая – из трех элементов.

Рис. 2.10. Логические схемы реализации выражения

Важные соотношения булевой алгебры можно получить, используя теорему де Моргана. Согласно этой теореме, выражения, характеризующие свойства конъюнкции и дизъюнкции переменных А, В и С, связаны между собой следующим образом:

(2.21а)

(2.21б)

Теорема де Моргана полезна при выполнении двойственных преобразований булевых выражений. Преобразование согласно этой теореме заключается во взаимной замене знаков Ú и Ù и замене всех переменных их дополнениями. Рассмотрим, например, трехвходовую схему И. Из (2.16) и (2.21а) получаем

(2.22)

Схема реализации этого выражения показана на рис. 2.11.

Рассмотрим пример упрощения выражения.

Пример 2.1. Выражение

можно упростить следующим образом:

		по теореме (2.19б)
		по теореме (2.15а)
		по теореме (2.12б)

Пример 2.2. Выражение

		по теореме (2.14б)
		по теореме (2.19а)
		по теореме (2.15б)
		по теореме (2.12а)
		по теореме (2.20б)

Рис. 2.11. Логическая схема реализации выражения

Комбинационные логические схемы

Выходные сигналы комбинационных логических схем опреде­ляются только значениями входных сигналов в любой данный мо­мент времени. Благодаря этой особенности разработка комбина­ционной схемы относительно проста. Первым шагом в процессе разработки является составление таблицы истинности, в которой для всех комбинаций входных сигналов указываются соответст­вующие выходные сигналы. С целью пояснения сказанного рас­смотрим, как реализуется логическая схема, выполняющая опера­цию ИСКЛЮЧАЮЩЕЕ ИЛИ (сложение по модулю 2), или операцию несовпадения. Эта схема особенно часто используется в арифметических сумматорах. Таблица истинности 2.6 описывает работу данной схемы. Сигнал на выходе принимает истинное значение только в том слу­чае, когда значения входных сигналов не совпадают.

Таблица 2.6.

Таблица истинности для схемы ИСКЛЮЧАЮЩЕЕ ИЛИ
А	В	X
0	0	0
0	1	1
1	0	1
1	1	0

В таблице истинности 1 соответствует переменной А (ИСТИ­НА), 0 – (ЛОЖЬ). Из таблицы видно, что значение Х на выхо­де истинно при следующих комбинациях входов А и В:и В или А и.

Это можно записать следующим образом:

(2.23)

Выражение (2.23) известно как выражение для получения суммы произведений; последние называют минитермами. На рис. 2.12 изображена схема реализации операции ИСКЛЮЧАЮ­ЩЕЕ ИЛИ (2.23). В этой схеме используются элементы И, ИЛИ и НЕ. Поскольку любую функцию можно реализовать с использо­ванием указанных элементов, такую комбинацию элементов назы­вают функционально полной. Существуют другие функционально полные системы, например система, реализующая функцию И-НЕ, или система, реализующая функцию ИЛИ-НЕ.

Рис. 2.12. Логическая схема ИСКЛЮЧАЮЩЕЕ ИЛИ.

Операция ИСКЛЮЧАЮЩЕЕ ИЛИ обычно записывается как и читается«А исключающее или В». Соответствующие ус­ловные обозначения схемы представлены на рис. 2.13. Комбина­ционные схемы часто используются при преобразовании кодов.

Рис. 2.13. Условное обозначение Схемы ИСКЛЮЧАЮЩЕЕ ИЛИ.