
Г. А. Мальцева - Инженерная графика
.pdf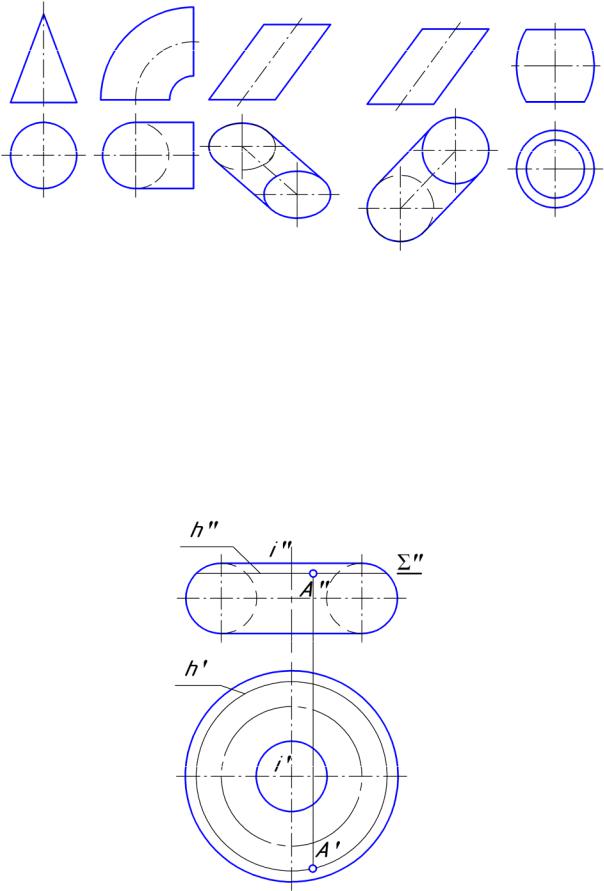
8.37. Соответствие изображений поверхностей их названиям:
Рис. 1 |
Рис. 2 |
Рис. 3 |
|
Рис. 4 |
Рис. 5 |
а) |
эллиптический цилиндр; |
г) |
конус вращения; |
|
|
б) |
открытый тор; |
|
д) |
наклонный цилиндр; |
|
в) |
параболоид; |
|
е) |
закрытый тор. |
|
Установите правильную последовательность:
8.38. Для нахождения горизонтальной проекции А' точки А по заданной ее фронтальной проекции А" нужно:
71
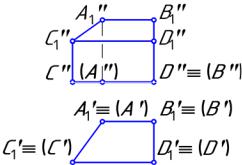
а) с помощью вертикальной линии связи найти горизонтальную проекцию А' точки А. А"А' ∩ h' = А';
б) через А" провести плоскость Σ (Σ"), замерить радиус окружности h", на которой находится проекция А" точки А;
в) на плоскости H провести горизонтальную проекцию h' окружности h.
9. МНОГОГРАННИКИ
Дополните:
9.1.Многогранником называют тело, ограниченное со всех сторон плоскостями. Эти плоскости называются ________________.
9.2.Общие стороны смежных граней многогранника называются ___.
9.3.Точки пересечения ребер многогранника называются _________.
9.4.Призма – многогранник, у которого основания – два равных и взаимно параллельных многоугольника, а боковые грани _____________.
9.5.Кратчайшее расстояние между основаниями призмы называется
_________.
9.6.Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а боковые грани ________ с общей вершиной S.
9.7.Боковую поверхность многогранника называют проецирующей, если она _________ одной из плоскостей проекций.
Выберите один правильный ответ:
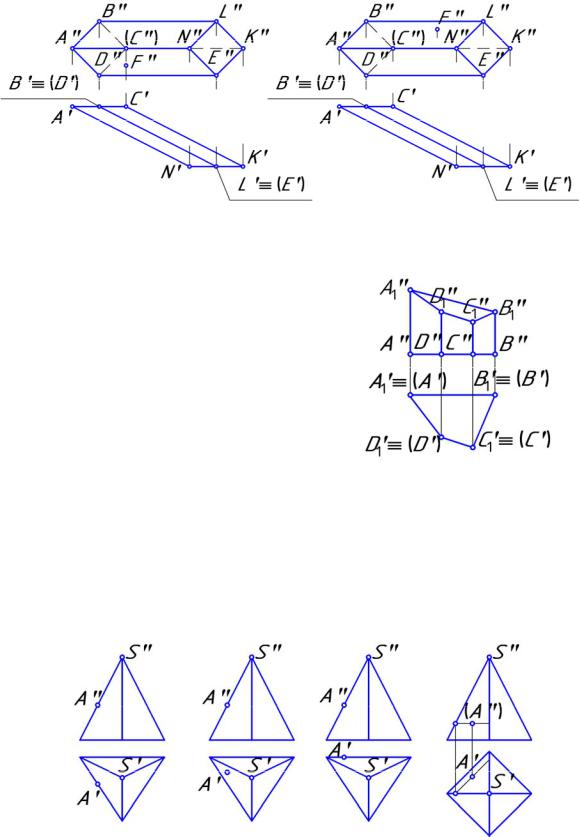
9.8. Профильной плоскостью является грань многогранника:
а) С1А1АС; б) А1В1ВА;
в) С1А1В1D1;
г) D1В1BD;
д) CABD.
72
9.9. Рисунок, на котором горизонтальная проекция точки F, принадлежащей поверхности призмы, видима:
Рис. 1 Рис. 2
9.10. Плоскостью общего положения является грань многогранника:
а) AА1D1D;
б) ABCD;
в) А1В1С1D1;
г) DD1CС1.
9.11. Форма сечения, если секущая плоскость пересекает три боковых ребра и основание четырехугольной пирамиды:
а) |
треугольник; |
в) |
пятиугольник; |
б) |
четырехугольник; |
г) |
шестиугольник. |
9.12. Рисунок, на котором точка А принадлежит поверхности:
Рис. 1 |
Рис. 2 |
Рис. 3 |
Рис. 4 |
73
9.13. Многогранная поверхность, все боковые ребра которой пересе-
каются в одной точке, называется: |
|
|
а) призматической; |
в) |
цилиндрической; |
б) пирамидальной; |
г) |
конической. |
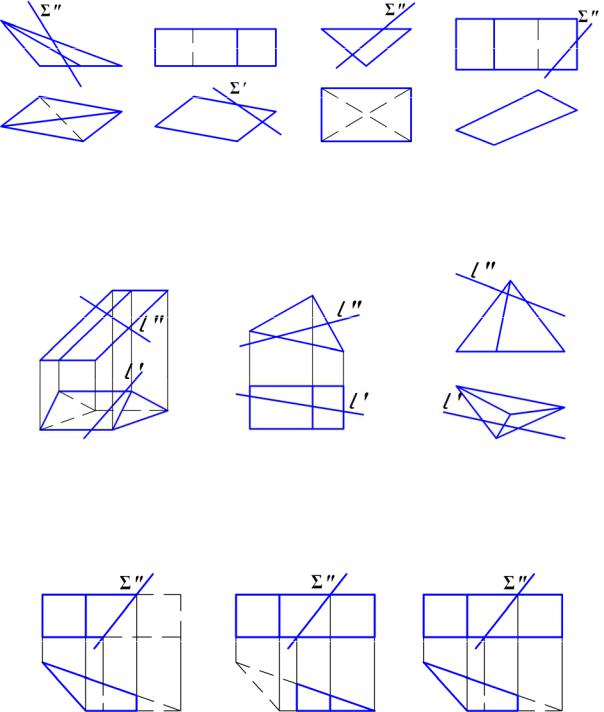
9.14. Рисунок, на котором сечение поверхности является треугольни-
ком:
Рис. 1 |
Рис. 2 |
Рис. 3 |
Рис. 4 |
9.15. Рисунок, на котором можно определить точки пересечения прямой l с многогранником без дополнительных построений:
Рис. 1 |
Рис. 2 |
Рис. 3 |
9.16. Рисунок, на котором правильно показана видимость призмы, пересекаемой фронтально проецирующей плоскостью Σ":
Рис. 1 |
Рис. 2 |
Рис. 3 |
|
74 |
|
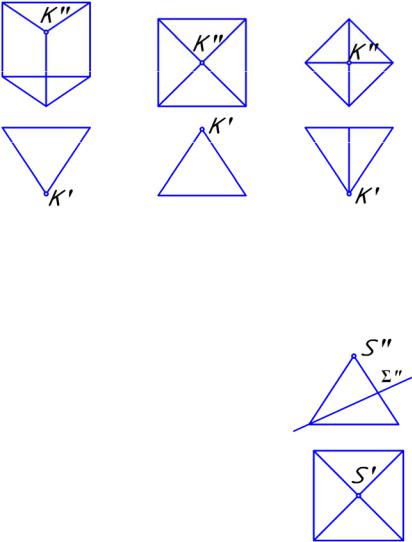
9.17. Рисунок, на котором правильно показана видимость рёбер многогранника:
|
Рис. 1 |
Рис. 2 |
Рис. 3 |
9.18. Форма сечения, получающаяся при сечении многогранника |
|||
плоскостью Σ: |
|
|
|
а) |
трапеция; |
|
|
б) |
прямоугольник; |
|
|
в) |
треугольник. |
|
|
Выберите несколько правильных ответов:
9.19. Для построения многоугольника сечения при пересечении многогранника плоскостью применяются два способа:
а) |
вершин; |
в) |
граней; |
б) |
рёбер; |
г) |
прямоугольного треугольника. |
9.20. К многогранникам относятся элементы: |
|||
а) |
образующие; |
г) |
грани; |
б) |
рёбра; |
д) |
оси вращения. |
в) |
вершины; |
|
|
|
|
|
75 |
Установите соответствие: |
|
|
|
9.21. Соответствие между названиями: |
|
|
|
а) |
куб; |
1) |
правильный тетраэдр; |
б) |
правильный восьмигранник; |
2) |
правильный гексаэдр; |
в) |
правильная трехгранная пирамида; |
3) |
правильный октаэдр; |
|
|
4) |
додекаэдр. |
Установите правильную последовательность:
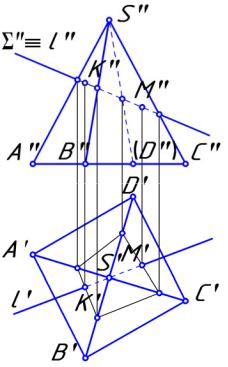
9.22. Для нахождения точек пересечения прямой l с пирамидой
SABCD нужно:
а) найти точки пересечения заданной прямой l со сторонами многоугольника сечения на горизонтальной плоскости проекций;
б) с помощью линий связи найти проекции точек пересечения прямой l с пирамидой SABCD на фронтальной плоскости проекций;
в) через заданную прямую l провести вспомогательную плоскость – посредник Σ (Σ");
г) найти горизонтальную проекцию многоугольника сечения пирамиды плоскостью Σ (Σ").
76
10. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
Дополните:
10.1.Линия пересечения двух кривых поверхностей в общем случае представляет собой ________ кривую.
10.2.Концентрические сферы–посредники следует применять, если оси поверхностей вращения пересекаются, а их общая плоскость симметрии ____________ плоскости проекций.
10.3.За центр концентрических сфер принимают точку пересечения
__________ пересекающихся поверхностей.
10.4.Радиус минимальной сферы Rmin должен быть равен радиусу сферы, ____________ одной из поверхностей и пересекающей другую.
10.5.Для построения линии пересечения двух многогранников используют способ ребер и способ ____________ .
10.6. Если две поверхности второго порядка касаются друг друга в двух точках, то линия их пересечения распадается на две _________ кривые второго порядка.
Выберите один правильный ответ:
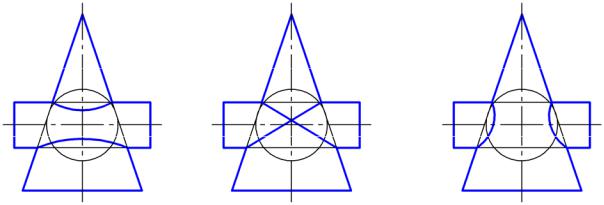
10.7. Рисунок, на котором правильно построена линия пересечения конуса и цилиндра, оси которых расположены в одной фронтальной плоскости:
Рис. 1 |
Рис. 2 |
Рис. 3 |
77
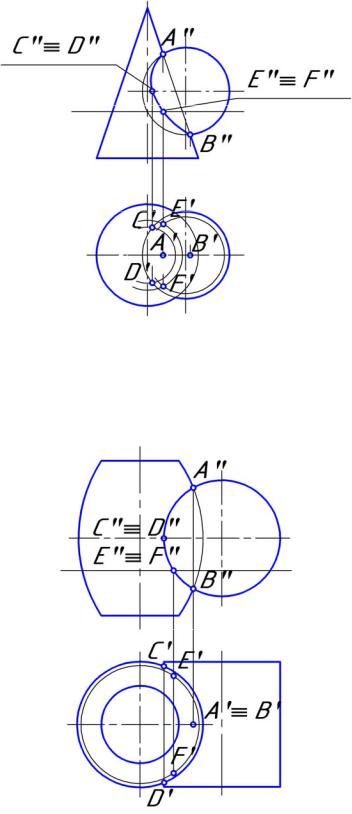
10.8. Точками границы видимости на горизонтальной плоскости проекций являются точки линии пересечения поверхностей:
а) E и F;
б) E и C;
в) C и D; г) А и В.
10.9. Точками границы видимости на фронтальной плоскости проекций являются точки линии пересечения поверхностей:
а) А и В; б) В и С; в) С и D; г) Е и F.
78
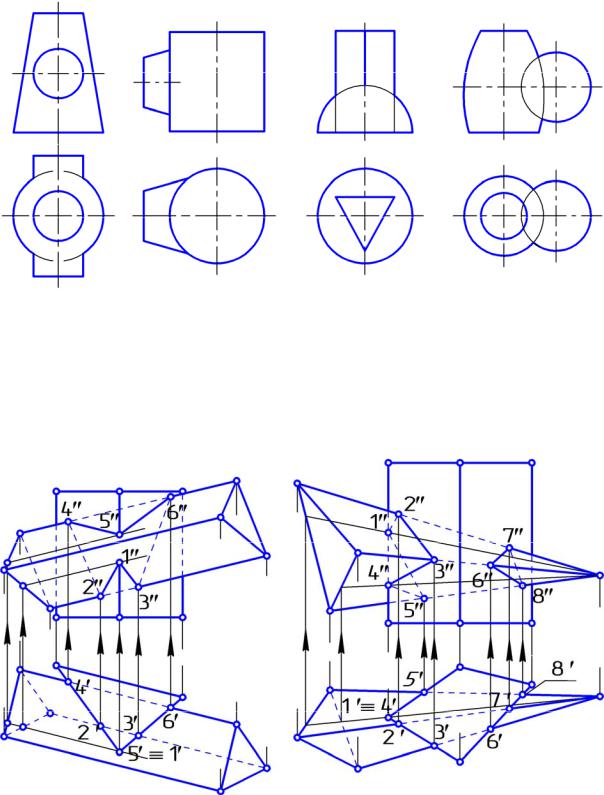
10.10. Рисунок, на котором изображены поверхности, линия пересечения которых состоит только из плоских кривых:
Рис. 1 |
Рис. 2 |
Рис. 3 |
Рис. 4 |
10.11. Рисунок, на котором при пересечении двух многогранников образуются две замкнутые линии (случай проницания):
Рис. 1 |
Рис. 2 |
79
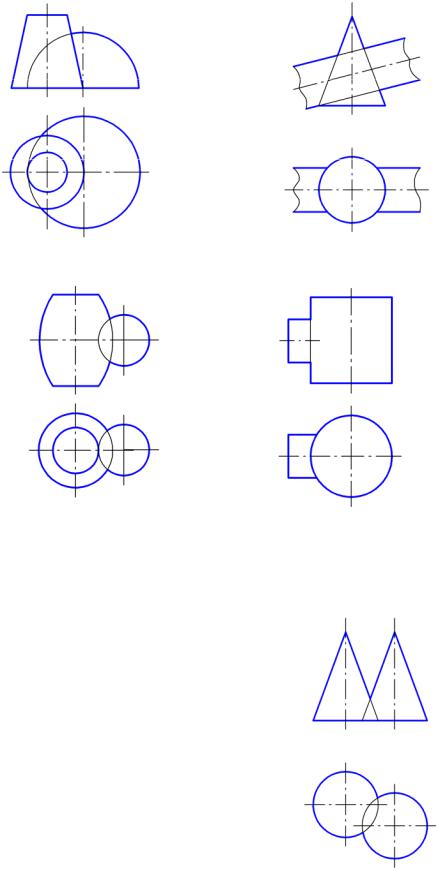
10.12. Рисунок, на котором изображены поверхности, линию пересечения которых нельзя построить способом секущих плоскостей:
Рис. 1 |
Рис. 2 |
|
Рис. 3 |
Рис. 4 |
10.13. Плоскости, |
при помощи которых рациональнее строить линию |
|
пересечения данных поверхностей: |
||
а) |
фронтальные; |
|
б) |
горизонтальные; |
|
в) |
профильно проецирующие. |
|
80
