ОТИ практическая 2

«Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева» (СибГАУ)

Аэрокосмический колледж

Преподаватель: Пятков Антон Геннадьевич, СибГАУ

Основы теории информации

Практическая работа № 2

«Поиск энтропии случайных величин»

Цель: закрепить теоретические знания и получить практические навыки при вычислении энтропии.

Теоретическая часть

Рассмотрим некоторую систему Х, которая может принимать конечное множество состояний х₁, х₂, ... х_n. Вероятность возникновения каждого состояния р₁, р₂, ... р_n.

Примером системы Х может быть алфавит, у которого под множеством состояний понимаются символы алфавита

В качестве меры неопределенности этой системы в теории информации применяется специальная характеристика, называемая энтропией.

Энтропией системы может быть определена как сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком.

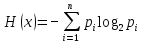(1)

Энтропия обладает рядом свойств:

1. Энтропия системы всегда больше нуля.

2. Энтропия обращается в ноль, когда одно из состояний достоверно, а другие невозможны.

3. Энтропия принимает максимальное значение, когда все состояния равновероятны.

4. Энтропия обладает свойством аддитивности, когда несколько систем объединяются в одну, их энтропии складываются.

Рассмотрим простейший случай. Система имеет два состояния и эти состояния равновероятны.

хi	х1	х2
рi	0,5	0,5

По формуле (1) имеем:

Н(х)=-(0,5log₂ 0,5+0,5log₂0,5)=1 бит/символ

Логарифм в формуле может быть взят при любом основании а>1. Выбор основания равносилен выбору определенной единицы измерения энтропии. На практике удобнее всего пользоваться логарифмами при основании два и измерять энтропию в двоичных единицах или битах. Таким образом, это энтропия одного двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.

ЭНТРОПИЯ СЛОЖНОЙ СИСТЕМЫ

Под объединением двух систем X и Y с возможными состояниями x₁, x₂, …, x_n, y₁, y₂, …, y_m понимается сложная система (X, Y), состояние которой (x_i,y_j) представляют собой все возможные комбинации состояний x_i,y_j . При этом число возможных состояний системы (X, Y) равно nm.

В качестве примера сложной системы может быть взят алфавит, имеющий двухбуквенные сочетания. Обозначим p_ij вероятность того, что система (X, Y) будет находиться в состоянии (x_i,y_j). Тогда вероятности p_ij можно представить в виде таблицы.

	x1	x2	…	xn
y1	p11	p21	…	pn1
y2	p12	p22	…	pn2
…	…	…	…	…
ym	p1m	p2m	…	pnm

Энтропия сложной системы равняется сумме произведений вероятностей всех возможных ее состояний на их логарифмы с обратным знаком

.

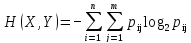Энтропию сложной системы, как и энтропию простой, тоже можно записать в форме математического ожидания

.

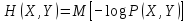Если системы X и Y независимы одна от другой, то при объединении систем их энтропии складываются .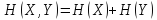

Это положение называется теоремой сложения энтропий.

УСЛОВНАЯ ЭНТРОПИЯ. ОБЪЕДИНЕНИЕ ЗАВИСИМЫХ СИСТЕМ

Пусть имеются две зависимые системы X и Y. Обозначим p(y_j|x_i) условную вероятность того, что система Y примет состояние y_j при условии, что система X находится в состоянии x_i.

Частная условная энтропия системы Y при условии, что система X находится в состоянии x_i определяется следующим образом

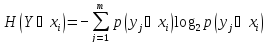. (2)

Для нахождения полной энтропии системы каждая частная энтропия умножается на вероятность соответствующего состояния р_i и все произведения складываются

,

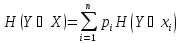где р_i – вероятность наступления события х_i.

Или

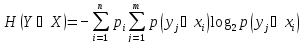(3)

После преобразований получаем

,

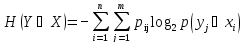где р_ij=р_ip(y_j|x_i).

Выражению также можно придать форму математического ожидания

.

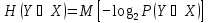Таким образом, полная энтропия характеризует степень неопределенности системы Y, остающейся после того, как состояние системы X полностью определилось.

Пользуясь понятием условной энтропии, можно определить энтропию объединенной системы через энтропию ее составных частей В этом случае теорема сложения энтропий для зависимых систем выглядит следующим образом.

Если две системы X и Y объединяются в одну, то энтропия объединенной системы равна энтропии первой ее составной части плюс условная энтропия второй части относительно первой

.

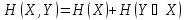В частном случае, когда системы X и Y независимы, H(X|Y) = H(Y), и мы получаем рассмотренную ранее теорему сложения энтропий

.

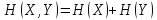В другом крайнем частном случае, когда состояние одной из систем полностью определяет собой состояние другой (или, как говорят, системы эквивалентны), получаем:

.

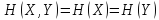Практическая часть

1. Рассчитать значение энтропии для несбалансированного 6-гранного игрального кубика, у которого распределение задается следующей таблицей:

X i	1	2	3	4	5	6
P i	1/11	1/15	1/17	1/(№ варианта)	1/(№ варианта + 13)	?

Значение p6 рассчитать также.

2. Рассчитать значение энтропии для сбалансированного 6-гранного игрального кубика.

3. Определить в каком случае (сбалансированный или несбалансированный кубик) больше энтропия и во сколько раз.

4. (не обязательное, на дополнительную оценку) Определить максимальное значение энтропии системы, состоящей из 8 элементов. Каждый элемент может находиться в одном из четырех состояний.

5