Компьютерная графика ч1

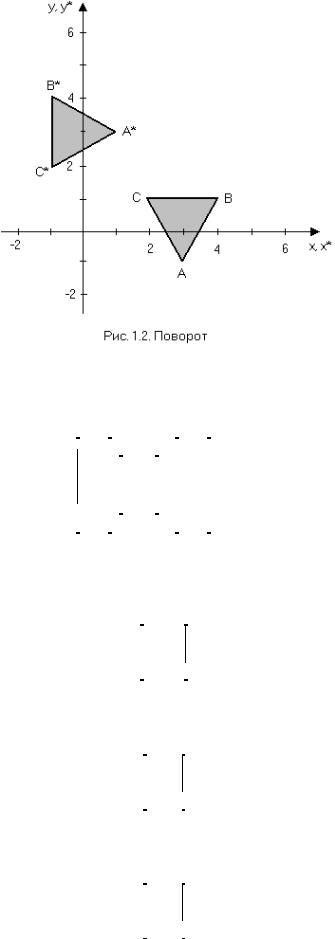
42

Если использовать матрицу (3 х 2), состоящую из координат x и y вершин треугольника, то можно записать

что является координатами результирующего треугольника A*B*C*. Поворот нв 180° относительно начала координат достигается путем следующего преобразования

а на 270° относительно начала координат - преобразованием

Разумеется, что матрица тождественного преобразования

43

соответствует повороту вокруг начала координат на 0° или на 360°.

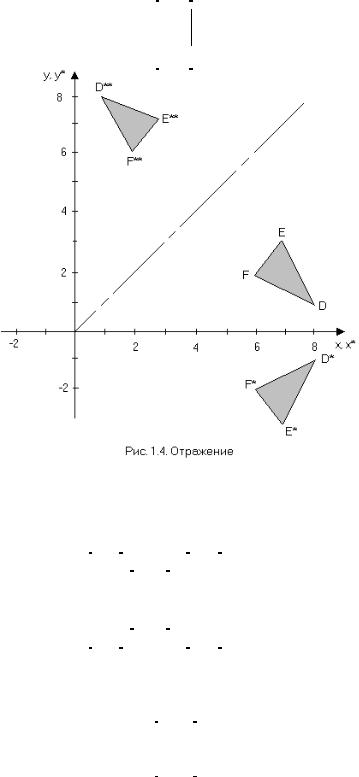
Как осуществить поворот вокруг точки начала координат на произвольный угол θ? Для ответа на этот вопрос рассмотрим вектор положения от начала координат до точки Р (рис. 1.3). Обозначим r - длину вектора, а φ - угол между вектором и осью х. Вектор положения поворачивается вокруг начала координат на угол θ и попадает в точку Р*. Записав векторы положений для Р и Р*, получаем:

Р = [х у] = [r cosφ r sinφ]

и

Р* = [x* у*] = [r соs(θ + φ) r sin(θ + φ].

Используя формулу для cos суммы углов, перепишем выражение для Р* следующим образом

Р* = [x* у*] = [r(cosφcosθ - sinφsinθ) r(соsφsinθ + sinφcosθ)].

Используя определения х и у, можно переписать Р* как

Р* = [x* у*] = [x cosθ - y sinθ x sinθ + y cosθ].

Таким образом, преобразованная точка имеет координаты x* = x cosθ - y sinθ

y* = x sinθ + y cosθ.

Или в матричном виде

[X*] = [X][T] = [x* y*] = [x y] cosθ sinθ

-sinθ cosθ

Итак, преобразование поворота вокруг точки начала координат на произвольный угол θ задается матрицей

[T] = cosθ sinθ -sinθ cosθ

44

Отражение

В то время как полный поворот на плоскости xy обычно осуществляется в двумерном пространстве относительно нормали к плоскости, отражение представляет собой тот же поворот на угол 180° в трехмерном пространстве и обратно на плоскость относительно оси, лежащей в плоскости xy. На рис. 1.4 приведены примеры двух отражений на плоскости треугольника DEF. Отражение относительно прямой y = 0 (ось x) получено с использованием матрицы

В этом случае новые вершины треугольника D*E*F* будут определяться

Подобным образом отражение относительно оси y при x = 0 будет иметь вид

45

Отражение относительно прямой y = x осуществляется с помощью матрицы

[T]= 0 1 1 0

Выполнив преобразования, получим координаты вершин треугольника D**E**F**

Аналогичным образом отражение относительно оси x будет иметь вид

[T]= 0 -1 -1 0

Масштабирование

Величина масштабирования определяется значением элементов исходной диагональной матрицы. Если матрица

[T]= 2 0 0 2

используется в качестве оператора воздействия на вершины треугольника, то имеет место «двукратное» расширение или равномерное масштабирование относительно точки начала координат. Если значения элементов не равны, то треугольник искажается, что проиллюстрировано на рис.1.5. Треугольник ABC, преобразованный с помощью матрицы

[T]= 2 0 0 2

переходит в пропорционально увеличенный треугольник A*B*C*. Тот же треугольник, но преобразованный с помощью матрицы

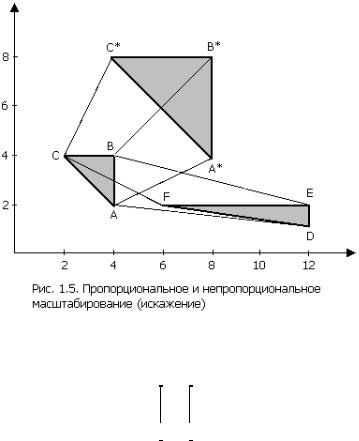
46

переходит в треугольник DEF, имеющий искажение, вызванное разными коэффициентами масштабирования.

В общем случае при матрице

[T]= a b c d

вкоторой а = d, b = с = 0, выполняется пропорциональное масштабирование; если a <> d, b = с = 0, то масштабирование будет проведено непропорционально. В первом случае для а

=d > 1 происходит расширение, т.е. - увеличение изображения. Если а = d < 1, то происходит равномерное сжатие, т.е. фигура уменьшается. Непропорциональное расширение и сжатие возникают в зависимости от значений a и d, которые могут быть меньше либо больше, чем 1, независимо друг от друга.

Перемещения и однородные координаты

В предыдущих разделах был рассмотрен ряд преобразований, совершаемых с помощью (2х2)-матрицы общего преобразования. Среди них поворот, отражение, масштабирование, сдвиг и другие. Ранее отмечалось, что исходная система координат инвариантна по отношению ко всем перечисленным преобразованиям. Однако возникает необходимость изменять положение начала координат, т. е. преобразовывать каждую точку на плоскости. Этого можно достичь путем перемещения точки начала координат или любой другой точки на плоскости

x* = ax + cy + m, y* = bх + dy + n.

К сожалению, нельзя ввести константы перемещения m и n в (2х2)-матрицу преобразования, так как это не пространство!

47

Данное затруднение можно преодолеть, используя однородные координаты. Однородные координаты неоднородного координатного вектора [x y] представляют собой тройку [x' y' h], где x = x'/h, y = y'/h, а h - некоторое вещественное число. Заметим, что случай h = 0 является особым. Всегда существует один набор однородных координат вида [х у 1]. Мы выбрали эту форму, чтобы представить координатный вектор [х y] на физической плоскости хy. Все остальные однородные координаты представляются в виде [hx hy h]. Данные координаты не сохраняют однозначности, например, все следующие координаты [6 4 2], [12 8 4], [3 2 1] представляют физическую точку (3,2).

Матрица преобразования для однородных координат имеет размер 3х3. В частности,

a b 0

[T]= c d 0 m n 1

где действие элементов а, b, с и d верхней части (2х2)-матрицы точно соответствует действиям, рассмотренным ранее. Элементы m и n являются коэффициентами перемещения в направлениях x и y соответственно. Полная двумерная матрица преобразования имеет вид

Отметим, что каждая точка плоскости и даже начало координат x = y = 0 теперь могут быть преобразованы.

Пространственные преобразования

Точка в трехмерном пространстве [х y z] представляется четырехмерным вектором

[x' y' z' h] = [x y z 1][T]

где [Т] является матрицей некоего преобразования. Как и ранее, преобразование из однородных координат в обычные задается формулой

Обобщенную матрицу преобразования размерности 4х4 для трехмерных однородных координат можно представить в следующем виде:

Матрицу преобразования 4х4 можно разделить на четыре отдельные части. Верхння левая (3x3)-подматрица задает линейное преобразование в форме масштабирования, сдвига, отражения и вращения. Левая нижняя (1х3)-подматрица задает перемещение, а правая верхняя (3х1)-подматрица - перспективное преобразование. Последняя правая нижняя (1х1)- подматрица задает общее масштабирование. Общее преобразование, полученное после применения этой (4 х 4)-матрицы к однородному вектору и вычисления обычных координат, называется билинейным преобразованием. В общем случае данное преобразование осуществляет комбинацию сдвига, локального масштабирования, вращения, отражения, перемещения, перспективного преобразования и общего масштабирования.

Лабораторные основы

Цель работы: научиться использовать матрицы для таких двумерных преобразований, как сдвиг, масштабирование, поворот, симметрия (отражение относительно произвольно заданной точки и отрезка).

Основные понятия, используемые в лабораторной работе: Однородные координаты. Двумерные преобразования (2D-преобразования). Матрицы. Суперпозиция простейших преобразований на языке матриц. Действия над матрицами.

Все изменения какого-нибудь объекта (кроме изменения цвета) на экране дисплея можно отнести к геометрическим преобразованиям, причем это относится и к изменениям при движении, и к статичным изменениям. Все превращения объекта можно представить как набор (суперпозицию) элементарных геометрических преобразований, выполненных в определённом порядке. В компьютерной графике всё, что относится к преобразованиям на плоскости, принято обозначать 2D, а к преобразованиям в пространстве - 3D.

Двумерные преобразования на плоскости

Сдвиг

На ху-плоскости есть точка Р с координатами (1,1). Сдвинем (перенесём) эту точку на новую позицию с координатами (2,6). Какие параметры этого простого геометрического преобразования? Параметра два: сдвиг по оси х, равный 1=2-1, и сдвиг по оси у, равный 5= 6- 1.

Масштабирование

На ху-плоскости есть точка Р с координатами (2,6) (это точка из предыдущего примера). С помощью операции масштабирования вернём её на прежнее место, то есть на (1,1). Итак, во сколько раз надо сжать координаты точки Р? Очевидно, что по оси х в 2/1=2 раза, а по оси у в 6/1= 6 раз . Или растянуть в 1/2 и 1/6 раза соответственно.

49

Поворот

На ху-плоскости есть точка Р с координатами (1,1). Повернём точку Р относительно начала координат на угол φ=180°. Найдём её новые координаты. Получим, даже не прибегая к вычислениям (-1,-1). А если, например, φ = 25°, то "на глазок" получить новые координаты точки уже не получится. Выведем уравнения поворота точки на произвольный угол относительно начала координат. Пусть точка Р (х,у) поворотом на угол φ переводится в точку Р'(х',у'). В системе координат в Visual Basic углы по часовой стрелке - положительны. Поворот выполняется относительно начала координат, расстояния от него до точек Р и Р' пусть равны r. Получаем следующие соотношения.

Для точки Р: х = r cos α , у = r sin α .

Для точки Р': х' = r cos (α + φ) = r cos α cos φ - r sin α sin φ, у' = r sin (α + φ) = r cos α sin φ + r sin α cos φ.

х' = х cos φ - у sin φ у' = х sin φ + у cos φ

Однородные координаты

Однородными координатами точки называется тройка одновременно не равных нулю

чисел.

В компьютерной графике однородные координаты вводятся так: произвольной точке Р(х, у) на плоскости ставится в соответствие точка Р(х, у, 1) в пространстве.

Соединим прямой точки О(0, 0, 0) и Р(х, у, 1). Любую точку этой прямой, соединяющей начало системы координат О(0, 0, 0) с точкой Р(х, у, 1), можно задать тройкой чисел (hx, hy, h), где h≠0. Проведём плоскость z = 1, параллельную плоскости ху, через точку Р(х, у, 1). Прямая, соединяющая точки О и Р, пересекает плоскость z = 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху. Таким образом, между произвольной точкой с координатами (х, у) и множеством троек чисел (hx, hy, h), где h≠0, устанавливается взаимно однозначное соответствие, позволяющее считать числа hx, hy, h новыми (однородными) координатами этой точки. В компьютерной графике вслед за проективной геометрией для однородных координат принято обозначение:

х : у : 1

или в более общем случае:

х1 : х2 : х3 (числа х1, х2, х3 не должны быть равны нулю одновременно).

Однородные координаты удобны для программирования геометрических преобразований. При помощи однородных координат и матриц 3-го порядка можно выполнить любое геометрическое преобразование в плоскости. Любое геометрическое преобразование выполняется следующим действием:

a b 0 (x', y', 1) = (x, y, 1) c d 0 e f 1

50

x'=xa+yc+1e; y'=xb+yd+1f

Для каждого геометрического преобразования существует своя матрица.

Рассмотрим конкретный пример сдвига. На ху-плоскости есть точка Р с координатами (1,1). Требуется сдвинуть (перенести) эту точку на 1 единицу по оси х и на 5 единиц по оси у. Для сдвига существует следующее матричное выражение:

Здесь dx=1, dy=5. Следовательно, получаем: x'=1×1+1×0+1×1=2; y'=1×0+1×1+1×5=6

Суперпозиция

На примере поворота некоторой фигуры относительно заданной точки, рассмотрим множественные преобразования с помощью матричных выражений.

α

yв

xв

Для этого необходимо вначале переместить фигуру в начало координат, затем повернуть на необходимый угол α и вернуть обратно в точку вращения. Пусть координаты

51

Краткая информация из тригонометрии

Формулы сложения

Cos(α+β) = cos α cos β - sin α sin β Sin(α+β) = sin α cos β - cos α sin β

Некоторые значения тригонометрических функций

Матрицы преобразований на плоскости. Общий вид

1. Матрица сдвига (translation)

dx - сдвиг по оси х, dy - сдвиг по оси у

2. Матрица масштабирования (dilatation)

sx - коэффициент растяжения/сжатия по оси х; sy - коэффициент растяжения/сжатия по оси у. Если sx = sy - масштабирование однородно и пропорции объекта сохраняются. Если

- масштабирование неоднородно и пропорции объекта не сохраняются.

3. Матрица поворота (rotation)

φ - угол поворота объекта относительно начала координат.

4. Матрица симметрии (reflection)

Матрицы преобразований в пространстве. Общий вид