
Компьютерная графика ч1
.pdf21
Часть 2" Работа с мышью. Графический редактор "
Математические основы
Эта лабораторная работа предполагает создание маленького графического редактора. Что обычно умеет делать простейший графический редактор? Рисовать линии разной толщины и различных цветов на фоне, цвет которого мы можем изменять по нашему выбору. Значит, мы должны научить наш редактор изменять толщину линий, переключать цвета для линий и фона и, конечно, стирать нарисованное.
Программируя действия мыши, можно «заставить» появляться и исчезать курсор мыши, рисовать или, наоборот, запрещать рисование в зависимости от того, какая клавиша мыши нажата.
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАБОТЫ
В этой лабораторной работе делается попытка написать свой графический редактор. С имеющимися в нашем распоряжении возможностями может получиться редактор с небольшим набором инструментов, но похожий на стандартный редактор Windows Paint.
1.Запустить графический редактор Paint. Выполнить в нем самые простые
операции, например, изменить цвет фона, выбрать цвет рисования, выбрать инструмент рисования и нарисовать несколько линий разной толщины. Это нужно для того, чтобы вспомнить приемы работы в графическом редакторе, а затем написать фрагменты программы в нашем редакторе, которые обеспечат реализацию похожих инструментов: Тонкость и Ластик. Закрыть Paint без сохранения файла.
ЧАСТЬ I. "Установка основных параметров для рисования"
1.Выбрав Цвет фона и Цвет рисования, изменив толщину рисования, нарисовать на форме несколько линий. Всегда начинать рисование со щелчка мышкой по кнопке "Разрешить/Запретить рисование мышью" !!!
2.В процедуре "Тонкость" дописать строку реализации уменьшения толщины рисования (по аналогии с процедурой "Толщина").
3.В процедуре "Ластик" вписать строку реализации ластика.
ЧАСТЬ II "Основные события мыши" Существуют 3 основных события мыши:
Событие MouseDown происходит, когда нажата одна из кнопок мыши(левая или правая).
Событие МоusеМоve происходит, когда перемещаем указатель мыши.
22
Событие MouseUp происходит, когда отпускаем кнопку мыши.
Написать фрагменты программы в процедурах этих событий, чтобы на форме появлялись визуальные подтверждения этих событий (например, цепочка окружностей и т.д.). В редакторе можно комбинировать использование клавиатуры и мыши. Пример использования
см. в процедуре Form_MouseMove: здесь используется клавиша SHIFT.
ЧАСТЬ III "Создание кисти"
В этой части лабораторной работы написать фрагмент программы (в процедуре Form_MouseMove), который реализует кисть. Здесь наш редактор будет похож на Adobe Photoshop. Кисть - это в общем случае инструмент, содержащий некое изображение, которое является как бы мазком кисти. Мы должны понимать, что даже очень сложное изображение - это сочетание примитивов: точек, линий, основных геометрических фигур (окружности, квадраты и т.д.). При перемещении мыши мазок кисти, а значит и созданное нами изображение многократно повторится на форме.
23
Лабораторная работа № 2:
Часть 1"Простейший алгоритм построения отрезка и окружности. Алгоритм Брезенхема для построения отрезка и окружности"
Математические основы
Экран дисплея - это экран растрового дисплея. Экран - это решетка с практически невидимыми глазу отдельными ячейками. Ячейки решётки называются пикселями. Очевидно, что чем меньше ячейка ( пиксель ), тем более чётким получается изображение. Принято говорить не о размере решётки или размере пикселя, а о разрешении экрана. Разрешение экрана - это количество пикселей на экране. Например, разрешение экрана может быть 640 х 480 пикселей, 1024 х 768 пикселей и т.д.
Для того, чтобы на экране появилось какое-либо изображение, надо определённым цветом высветить определённый набор пикселей. То есть ответить на вопросы:
Где на экране высветить пиксель ( то есть где на экране поставить точку ) ? Каким цветом высветить этот пиксел?
Какие пиксели высветить, чтобы получить требуемое изображение?
Рис. 1 Построение растрового изображения на экране дисплея
Когда мы рисуем отрезок на бумаге, то это просто непрерывная линия, соединяющая две точки. Рисование отрезка на экране - это выбор на каждом шаге пикселя, который надо подсветить, чтобы в итоге цепочка посвеченных пикселей создала иллюзию линии, соединяющей конечные точки отрезка. Для вертикальных, горизонтальных и наклонённых под углом 45° отрезков выбор пикселей очевиден. Если угол наклона - другой, то требуется сформулировать правила, которые бы позволили выбирать пиксели для рисования отрезка ( или кривой, если говорить в общем случае ).
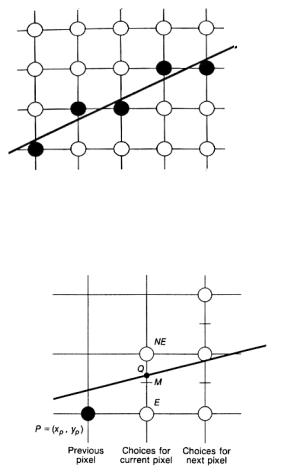
24
Рис.2 Выбор пикселей при построении отрезка на экране .
Существуют алгоритмы ( и появляются новые ) рисования отрезков. Естественно, что все эти алгоритмы - разные, но есть несколько правил, общих для всех алгоритмов:
1.Отрезки должны начинаться и заканчиваться в заданных точках.
2.Отрезки должны выглядеть прямыми .
3.Яркость вдоль отрезка должна быть постоянной, не зависеть от длины и наклона. 4. Рисовать надо быстро, чтобы глаза воспринимали отрезок как единое целое,
ане как
цепочку бегущих пикселей.
Простейший алгоритм построения отрезка
Рассмотрим задачу построения отрезка на растровой плоскости, соединяющего точки P(x1, y1) и Q(x2, y2). Зеркальным отображением мы всегда сможем добиться, чтобы
0 y2 y1 x2 x1
Это несколько упростит нашу задачу.
Существует несколько подходов, зависящих от представления отрезка. Мы можем использовать математическое задание:
y y |
y2 y1 |
(x x ), x x , x |
|
|
|
|
2 |
||||
1 |
x2 x1 |
1 |
1 |
|
|
|
|
|
|
|
|
Основные |
недостатки |
этих алгоритмов |
|||
очевидны. Это использование операций с вещественными числами и слишком сложные вычисления для построения обычного отрезка.
Алгоритм Брезенхема для построения отрезка.
Каждый пиксель имеет 8 соседей N, NE, NW, W, E, SE, SW, S. Предположим, что во время построения отрезка, мы поставили некоторую точку M (x,y). Тогда следующим мы поставим либо E либо NE пиксел. Как определить, какой из двух вариантов наиболее точно будет продолжать линию? Это можно определить с помощью срединной точки (рис.1) Если отрезок проходит выше срединной точки, то следующим ставится NE пиксел, иначе, если отрезок проходит ниже срединной точки, то ставится E пиксел. Сделать это математически поможет формула отрезка в неявно заданном виде:
F (x, y) (x x1 )dx ( y y1 )dy dx x2 x1
dy y2 y1
F(x,y)=0 – значит точка (x,y) лежит на отрезке F(x,y)<0 – выше отрезка
25
F(x,y)>0 – ниже отрезка
Предположим, мы поставили точку P. тогда координаты срединной точки
(xp 1, y p 1/ 2)
будут
А значение функции F в этой точке d F(xp 1, y p 1/ 2)
Если следующим поставленным пикселем будет E, тогда значение функции в новой срединной точке будет:
dnew F (x p 2, y p 1/ 2)
dnew dold F (x p 2, y p 1/ 2) F (x p 1, y p 1/ 2)
d dnew dold dy y2 y1
В случае NE:
dnew F (x p 2, y p 3 / 2)
d dy dx ( y2 y1 ) (x2 x1 )
Рассмотрим начальную точку (x1,y1):
dstart F (x1 1, y 1 1/ 2) (x1 1 x1 )dy ( y1 1/ 2 y1 )dx
dy dx / 2
Получив начальное значение d, мы сможем определить по его знаку положение следующего пикселя. Прибавив соответствующее d, мы получим значение функции для новой срединной точки и поставим второй пиксел. Продолжая цикл мы построим весь отрезок.
Единственная неприятность – деление на 2 в первом d. Получившееся значение скорее всего будет вещественным и потребует использование вещественных операций. Однако от этого можно избавиться, использовав следующее преобразование:
F ' (x, y) 2F (x, y) d ' 2d
d start 2dy dx
d ' 2 d
Тогда все d становятся целыми
Для построения произвольного отрезка перед построением необходимо проверить угол наклона и провести соответствующую зеркальную симметрию:
Если 0<=x2-x1<=y2-y1 то меняем местами x и y координаты.
Если тангенс угла наклона меньше 0, то отражаем относительно оси ординат x=-x а затем, если это необходимо, меняем x и y координаты.
Некоторые дополнительные вопросы построения отрезка
Порядок конечных точек
Одна из сложностей, возникающих по ходу построения отрезка, заключается в том, что отрезок от Т1 до Т2 должен содержать те же самые пиксели, что и отрезок Т2 – Т1, для
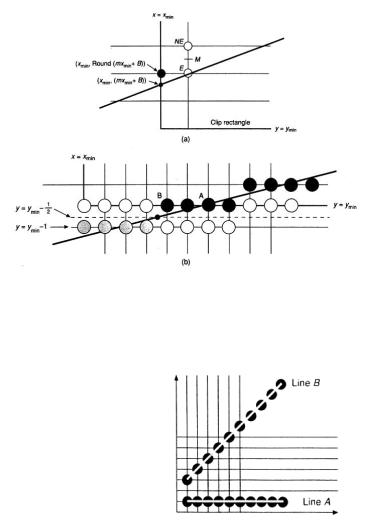
26
того, чтобы представление линии было независимо от порядка задания концов. Единственный случай, в котором выбор пикселя зависит от направления построения линии, это прохождение отрезка точно через срединную точку, т.е. когда индикатор d равен нулю. Строя линию слева направо мы выберем пиксель E, а в противном случае пиксель W, но он же расположен на единичку выше первого! А значит, при построении линии справа налево необходимо в случае d=0 выбирать SW – пиксел.
Альтернативный способ решения проблемы – менять местами концевые точки, чтобы сканирование линии проходило всегда в одном направлении. Но этот метод не работает в случае использования стилей линии. Маска стиля всегда присоединяется к нижней левой точке, в независимости от направления, что не всегда приводит к ожидаемому эффекту. Кроме того, при построении примитива, один сегмент может быть построен с маской, расположенной слева направо, а следующий – с маской справа налево, и в общей вершине появляется артефакт.
Построение отрезка в случае отсечения (клипирования)
Некоторая модификация алгоритма необходима для поддержки отсечения. На рисунке (a) показан отрезок, отсекаемый по левой границе клипирующего прямоугольника (x =min x). Точка пересечения с границей имеет целую x координату, но вещественную y.
Пиксель (xmin , Round (mxmin B)) - тот же самый, который был бы выведен в отсутствии отсечения. Однако, приняв этот пиксель в качестве начального, нам необходимо соответствующим образом инициализировать индикатор по следующей срединной точке. Это требуется для получения правильной
растеризации. В противном случае она была бы отлична от ожидаемой, ведь наклон нового отрезка от (xmin , Round (mxmin B)) до (x,y) не совпадает с наклоном исходного .
Еще более сложная ситуация представлена на рисунке (b) при пересечении отрезка с горизонтальной границей. Нам бы хотелось, чтобы были выведены все точки, соответствующие границе. Однако при простом вычислении точки пересечения отрезка и границы
будет поставлена в качестве первой точка A, а не B. Из рисунка видно, что первая точка, которую необходимо поставить – это ближайшая справа к точке пересечения отрезка с горизонталью
y ymin |
1/ |
2 . |
Значит, для правильного отсечения по нижней |
границе |
достаточно найти точку пересечения с линией |
||
y ymin |
1/ |
2 |
и округлить значение x. Таким образом, первый |
пиксель B будет расположен в (Round (xymin 1/ 2 ), ymin ) .
Растровые алгоритмы построения окружности.
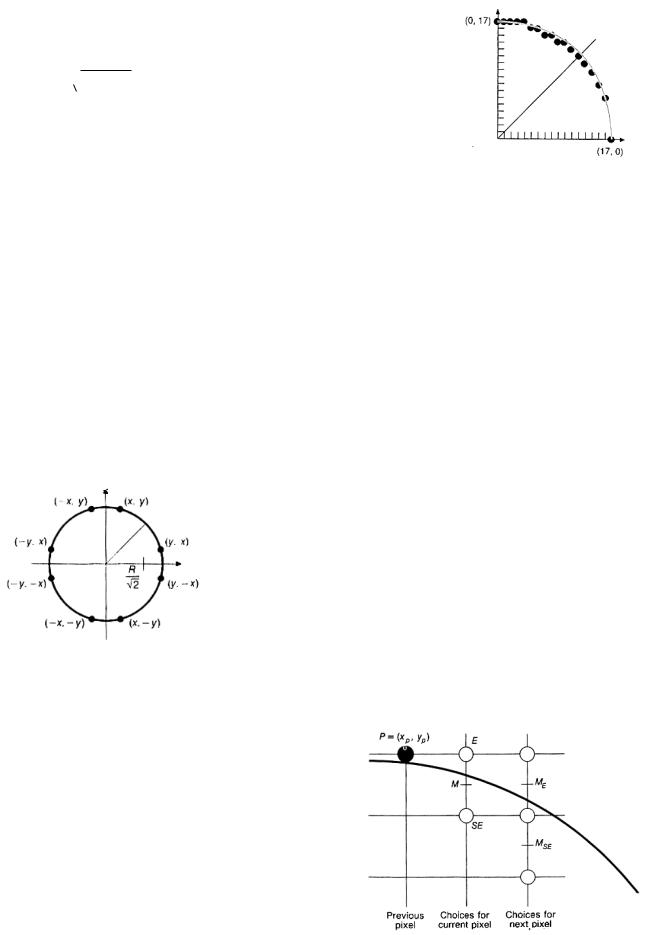
27
Окружность, как и отрезок, можно построить в лоб, используя математическое представление:
R 2 x 2 y 2 R 
 x 2 y 2
x 2 y 2
Тогда для каждого значения по оси абсцисс мы сможем вычислить соответствующее ему значение по ординате и поставить точку.
У данного метода существует несколько
недостатков:
-Слишком сложные вычисления (операция извлечения корня квадратного)
-Пиксели неравномерно распределяются по окружности, и она оказывается неравномерно освещенной
От второго недостатка можно избавиться, если использовать представление окружности в полярных координатах:
x R cos y R sin
Тогда, пробегая все возможные значения с заданным шагом, для каждого из них мы определим координаты соответствующего ему пикселя, и закрасим его. На этот раз, т.к. мы каждый раз поворачиваем радиус на один и тот же угол, то пиксели будут равномерно распределены по окружности (рис.5). Однако, как и в предыдущем алгоритме, вычисление операции cos и sin слишком трудоёмки.
Задачу можно значительно упростить, если использовать то, что окружность является центральносимметричной фигурой, а значит, если построить, к примеру, одну восьмую ее часть, то с помощью преобразования симметрии, можно достроить окружность полностью (рис.6).
Тогда можно использовать метод срединной точки для построения дуги окружности. Если за первый в дуге взять самый верхний пиксел, то следующим может быть лишь Е или SE пиксел. И это
справедливо для каждого пикселя в дуге. Если линия проходит выше срединной точки, то следующим пикселем будет E, если ниже – то SE.
Как и в случае отрезка, будем использовать задание окружности в неявном виде с помощью функции F(x,y):
Если F=0, то точка с данными координатами (x,y) расположена на окружности,
F(x, y) x2 y 2 R2
если больше нуля – то вне окружности. А если меньше нуля – то внутри окружности.
(xp , y p )
Пусть |
поставленная |
точка |
имеет |
28
координаты:
Вычислим значение в соответствующей ей срединной точке: dold F(xp 1, y p 1/ 2)
Если это d меньше нуля, т.е. окружность проходит выше срединной точки, то выбирается пиксель E, иначе выбирается пиксель SE.
Рассмотрим два случая (для двух различных выборов пикселя):
|
1) |
Если выбран пиксель E: |
|
||
dnew |
f (x p |
2, y p |
1/ 2) dold (2x p |
3) |
|
d E |
(2x p |
3) |
|
|
|
|
2) |
Если |
выбрали пиксель SE, то он имеет координаты (x+1,y-1), а значит, |
||
соответствующая ему исрединная точка (x+2,y-3/2). И тогда:
dnew dold (2x p 2 y p 5)
dSE (2x p 2 y p 5)
Таким образом, начиная с самой первой точки (верхняя точка окружности), мы определяем значение d для каждого нового пикселя, и, сравнив его значение с нулем, строим следующий пиксель в дуге окружности.
Рассчитаем значение d в начальной точке дуги (0,R):
F (1, R 1/ 2) 1 (R2 R 1/ 4) R2 5 / 4 R
d0 5 / 4 R
Значение d получается вещественным, что требует использования вещественных операций, которых желательно было бы избежать. Сделав замену h=d-1/4, получим, что h=1-R. Тогда необходимо сравнивать h с -1/4, но так как приращения d – целые числа, то сравнение можно заменить сравнением с нулем.
Построение дуги завершим, когда x станет примерно равен у. Вопрос с граничными точками соединения дуг решается отдельно в каждой реализации. Эти точки могут просто дублироваться.
Лабораторные основы
Цель работы: понять общие принципы построения изображения на примерах использования простейшего алгоритма построения отрезка, окружности и алгоритмов
Брезенхема.
В этой работе будет выполнено:
1). рисование отрезка прямой линии, проходящего из точки с координатами ( xl, yl ) в точку с координатами ( х2, у2 ), реализуя простейший алгоритм,
2). рисование отрезка прямой линии, проходящего из точки с координатами ( xl, yl ) в точку с координатами ( х2, у2 ) по алгоритму Брезенхема для отрезка,
3). рисование окружности по простейшему алгоритму,
4). рисование окружности по алгоритму Брезенхема.
29
Часть 2" Построение кривых в форме Безье. Построение кривых в форме Фергюсона (Эрмита)"
Математические основы
Явный, неявный и параметрический вид задания функции.
Явный вид задания функции
у — f(x) - это явное выражение для у позволяет вычислять у при любом значении х (кроме описания вертикальных прямых , например, х=3 ) . Уравнение прямой линии у=2х+3 - пример явного задания функции.
Неявный вид задания функции
f(x,y)=0 - неявное задание функции от х и у.
Пример неявного задания функции - уравнение окружности х +у — 1 = 0 с радиусом г=1. Чтобы в этом случае получить явный вид задания функции, уравнение х + у - 1=0 надо разбить на два уравнения:
для верхней половины окружности получим у = + ( 1 - х ) для нижней - у = -
( 1 + х )
Параметрический вид задания функции
В параметрическом виде задания функции х и у являются равноправными и представляются в виде функций от вспомогательного параметра t, то есть x = x(t),
У = У(0)
Параметрический вид, например, для уравнения окружности с радиусом г=1 будет записываться следующим образом:
X = COS t
У = sin t, где t лежит в интервале 0 < t < 2% .
Представление контуров в машинной графике
Наиболее распространены три типа представления контуров в машинной графике:
1.Кусочно-линейный
2.Линейно-круговой
3.Полиномиальный
Каждый из них имеет свои преимущества и свои недостатки.
1.Кусочно-линейный
По контуру кривой упорядоченно ( в порядке возрастания индекса !!! ) проставляются
точки, которые затем соединяются отрезками прямых. В результате получаем массивы координат:
xi,x2,x3,......... ,х„ и уьу2,уз, .......,Уп •
2.Линейно-круговой
Используется, как правило, в оборудовании с программным управлением, где контуры описываются с помощью отрезков и дуг окружностей. Название этого типа представления контуров говорит само за себя.
3. Полиномиальный
Явный вид задания полинома:
у = ао + aix + 32Х + + anxn
Параметрический вид задания полинома:
х = аОх + ajxt + a2xt2 + + anxtn у= аоу + aiyt + a2yt2 + ,... + anytn
Переход от представления контура в виде параметрической кубической кривой к кусочно-линейному представлению
Используется для упрощения вычисления размеров контура, например, для вычисления длины контура, площади внутри контура и т.д.
При конструировании пространственных форм (этим занимается геометрическое моделирование) возникают задачи трёхмерного представления поверхностей в пространстве. Рассмотрим одно из наиболее широко распространённых представлений, а , именно, параметрические кубические полиномы. Итак, почему кубический полином ( то есть кривая описывается многочленом третьей степени )? Потому что кубический многочлен является параметрической функцией наиболее низкой степени, с помощью которой можно представить кривую, описывающую реальную пространственную кривую. Имеется много способов представления параметрических бикубических кривых. Рассмотрим один из них: кривые Безье .
Преимущество параметрических кубических кривых - нет разрывов.
Кривые Безье
Безье (1970) перегруппировал члены параметрического кубического многочлена Фергюссона и получил кривую следующего вида:
r= r(t) = (l-t)3po + 3t(l-t)2Pl+3t2(l-t)p2 + t3p3 ,
0 < t < l
Ценность этой кривой в том, что для своего построения она требуют задания всего 4 точек. Две из четырех прямых, соединяющих эти четыре точки, будут являться касательными для кривой Безье и их взаимное расположение определяет форму кривой Безье.
Свойства кривой Безье
1.Кривая Безье является гладкой кривой.
2.Начинается в 1-ой вершине ро массива из четырёх точек р0, pi, рг, рз, касается отрезка popi и заканчивается в последней точке р3, касаясь отрезка ргРз-
3.Лежит в выпуклой оболочке, порожденной массивом точек р0, pi, p2, Рз-
4. Симметрична, то есть сохраняет свою форму при перемене порядка вершин массива на
противоположный : р0, рь р2, Рз Рз, Рг, Рн Ро •
5.Если точки ро, pi, P2, Рз лежат на одной прямой , то кривая Безье совпадает с отрезком
РоРз-
6.Если точки ро, pi, P2, Рз лежат в одной плоскости, то кривая Безье тоже лежит в этой плоскости.
7.Изменение положения хотя бы одной из четырёх опорных точек приводит к заметному изменению всей кривой Безье.
8.В уравнении, описывающем кривую Безье, нет свободных параметров - заданный набор из четырёх точек однозначно определяет кривую Безье, не давая возможности повлиять на её форму.
