Методические рекомендации

по проведению практических

занятий и выполнению контрольных работ

дисцеплина «Линейная алгебра»

Содержание

Введение………………………………………………………………………………….....3

Векторная алгебра и аналитическая геометрия на плоскости…………………..…4

Тема 1 Определители………………………………………………………………………4

Тема 2 Векторная алгебра……………………………………………………………….....7

Тема 3 Аналитическая геометрия на плоскости………………………………………...14

Аналитическая геометрия в пространстве…………………………………………..24

Тема 1 Плоскость в пространстве………………………………………………………..24

Тема2 Прямая в пространстве………………………………………………………… . 30

Тема 3 Поверхности второго порядка…………………………………………………...38

Системы линейных алгеброических уравнений………………………………...…..44

Тема2 Матрицы…………………………………………………………………………....44

Тема 3 Исследование и решение систем линейных уравнений методом Гаусса……..50

Тема 4 Обратная матрица………………………………………………………………...57

Введение

Практические занятия являются важной частью успешного освоения дисциплины «Линейная алгебра»

Студент должен успешно овладеть :

• основными понятиями аналитической геометрии и линейной алгебры;

• основными методами решения систем линейных уравнений;

• основными понятиями теории матриц и уметь применять их в конкретных ситуациях.

Настоящие рекомендации включают в себя достаточное количество примеров решения задач по темам рабочей программы курса «Линейная алгебра»,а также содержат конкретные рекомендации по решению задач и большое количество примеров для самостоятельной работы

Векторная алгебра и аналитическая геометрия на плоскости

Тема1 Определители( 4 часа)

Определителем матрицы ,

назовем число, соответствующее данной матрице и вычисляемое по определенному правилу

Его обозначают еще так:

,

Пусть дана квадратная матрица 3-го порядка

А =.

определитель - число, вычисленное по правилу

detА=.

Пример . Вычислить определитель второго порядка

detА3·5 - 2·1 = 15 - 2 = 13.

Пример . Вычислить определитель третьего порядка

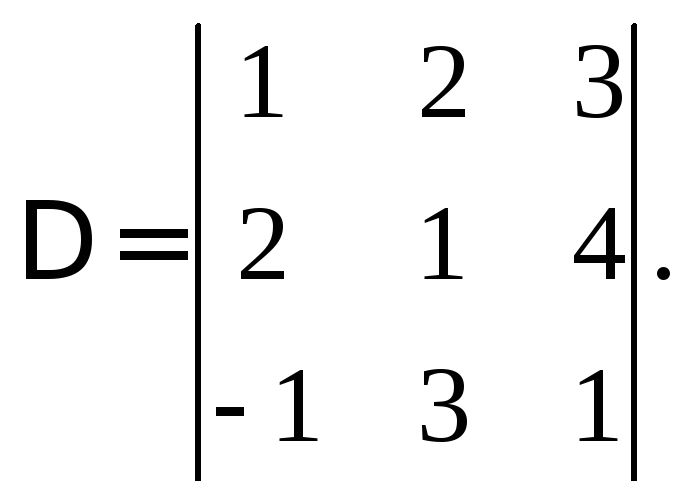
Решение

Способ 1. Разложив определитель по первой строке, получим

Способ 2.Вычислим теперь тот же определитель, используя свойства определителя.

К элементам второй строки прибавим соответствующие элементы первой, умноженные на (-2), а к элементам 3-й строки прибавим элементы первой строки, первую строку оставим без изменения (определитель не изменится):

Здесь произведены следующие действия: (1) - ко 2-й строке прибавили 3-ю; (2) - общий множитель второй строки вынесли за знак определителя; (3) - к 3-й строке прибавили 2-ю, умноженную на (-5). В результате получили определитель, под главной диагональю которого стоят нули (определитель верхнетреугольной матрицы). Такой определитель равен произведению элементов главной диагонали (можно разложить по первому столбцу). Итак, мы вновь получили тот же ответ = -2.

Этот способ выгодно использовать при вычислении определителей порядка n> 3

№ п/п	Умение	Алгоритм
1	Вычисление определи-теля методом Гаусса	Привести исходную квадратную матрицу к ступенчатому (верхнетреугольному) виду. Подсчитать число , равное числу перестановок строк при приведении матрицы к ступенчатому виду. Вычислить определитель матрицы . Определительравен произведению элементов главной диагонали ступенчатой матрицы, умноженному на множитель

Задание

Вычислить методом Гаусса определитель матрицы , где

^.

Решение

№ п/п	Алгоритм	Конкретное соответствие данного задания предложенному алгоритму
1	Приводим исходную матрицу элементарными преобразованиями к ступенчатому виду
2	Подсчитываем число K, равное числу перес-тановок строк при приведении к ступенчатому виду	K = 1, строки переставляли один раз
3	Вычисляем определитель ступенчатой матрицы как произведение элементов главной диаго-нали, умноженное на множитель	Угловые элементы ступенчатой матрицы совпадают с элементами главной диаго-нали

Решите самостоятельно следующие задания:

Вычислить определители заданных матриц.

Задание 1

Задание 2

^.

Задание 3

^.
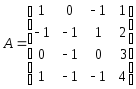