тест Математика-1 (3+3 рус) 2906
.docA)
B)
C)
D)
E)
107.
Найти расстояние между прямыми
и
:
A)
B)
C)
D)
E)
108.
Вычислить площадь треугольника,
отсекаемого прямой
от координатного угла:
A)
B)
C)
D)
E)
109.
Написать общее уравнение перпендикулярной
линии проходящей через середину
,
если
:
A)
B)
C)
D)
E)
110.
Даны
две точки на отрезке
и
.
Найдите на этом отрезке точку делящую
его в отношении
:
A)
B)
C)
D)
E)
111.
Даны точки
и
.
Найдите координаты середины отрезка
:
A)
B)
C)
D)
E)
112.
Составьте уравнение прямой, проходящей
через точку
параллельно прямой
:
A)
B)
C)
D)
E)
113.
Уравнение прямой, проходящей через две
заданные точки
имеет вид:
A)
B)
C)
D)
E)
114.
Написать общее уравнение прямой,
проходящей через точки
и
:
A)
B)
C)
D)
E)
115.
Определить значение
,
при котором прямые
и
будут перпендикулярны:
А)
В)
С)
D)
Е)
116.
Определить значение
,
при котором прямые
и
будут параллельны:
А)
В)
С)
D)
Е)
117.
Найти расстояние от т.
до прямой
:
А)
В)
С)
D) 7
Е) 5
118.
Определить координаты нормального
вектора
прямой
:
А)
В)
С)
D)
Е)
119.
Определить координаты направляющего
вектора
прямой
:
А)
В)
С)
D)
Е)
120.
Найти точку пересечения прямых
и
:
А)
В)
С)
D)
Е)
121.
Эксцентриситет эллипса
,
большая полуось равна 5. Найти расстояние
между фокусами:
А) 6
В) 3
С) 10
D) 15
Е) 12
122.
Определить координаты центра окружности
:
А)
В)
С)
D)
Е)
123.
Определить величину параметра р параболы
:
А)
В)
С)
D)
Е) 5
124.
Определить величину параметра р параболы
:
А) 1
В) 2
С)
D) –1
Е) –2
125.
Определить координаты фокусов гиперболы
:
А)
В)
С)
D)
Е)
126.
Найти эксцентриситет
эллипса
:
А)
В)
С)
D)
Е)
127.
В гиперболе оси равны
и
.
Найти уравнения асимптот:
А)
В)
С)
D)
Е)
128.
Найти полуоси эллипса
А)
В)
С)
D)
Е)
129.
Составить каноническое уравнение
гиперболы, если ее действительная
полуось равна
,
а мнимая полуось равна
А)
В)
С)
D)
Е)
130.
Найти уравнение директрисы параболы
А)
В)
С)
D)
Е)
131. .Каноническое уравнение эллипса имеет вид:
А)
В)
С)
D)
Е)
132..
Укажите координаты вершин
эллипса
:
А)
В)
С)
D)
Е)
133. Каноническое уравнение гиперболы имеет вид:
А)
В)
С)
D)
Е)
134. Уравнение асимптот гиперболы имеет вид:
А)
В)
С)
D)
Е)
135.
Эксцентриситет
эллипса, гиперболы вычисляется по
формуле:
А)
В)
С)
D)
Е)
136.
Уравнение директрисы параболы
имеет вид:
А)
В)
С)
D)
Е)
137.
Укажите координаты фокуса параболы
:
А)
В)
С)
D)
Е)
138.
Если
и
в
уравнении
,
то данное уравнение есть
А) уравнение окружности
В) уравнение эллипса
С) уравнение гиперболы
D) уравнение параболы
Е) уравнение лемнискаты Бернулли
139. Если ось симметрии параболы – ось ординат, то уравнение параболы имеет вид:
А)
В)
С)
D)
Е)
140. Если ось симметрии параболы – ось абсцисс, то уравнение параболы имеет вид:
А)
В)
С)
D)
Е)
141. Укажите общее уравнение плоскости в пространстве:
A)
B)
C)
D)
E)
142. Укажите общее уравнение прямой в пространстве:
A)
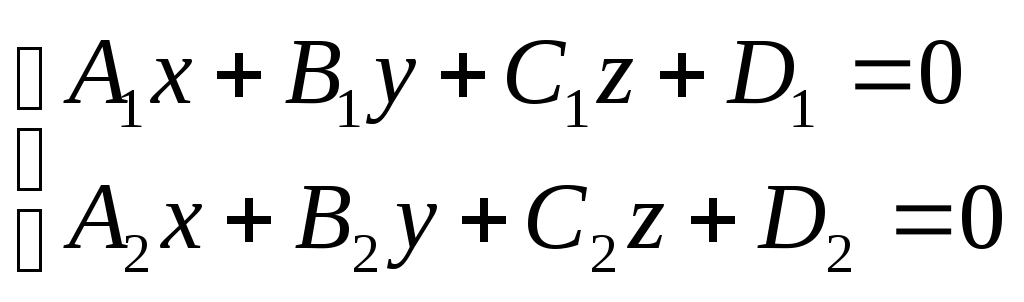
B)
C)
D)
E)
143. Укажите уравнение плоскости заданное точкой и нормальным вектором:
A)
B)
C)
D)
E)
144.
Угол
между прямой
и плоскостью
находится по формуле:
A)
B)
C)
D)
E)
145.
Дано уравнение плоскости
.
Указать вектор, перпендикулярный
заданной плоскости:
A)
B)
C)
D)
E) Перпендикулярного к заданной плоскости вектора нет
146.
Дано уравнение плоскости
.
Указать координаты точки пересечения
данной плоскости с осью абсцисс:
A)
B)
C)
D)
E)
147.
Уравнение плоскости, проходящей через
точку
перпендикулярно вектору
имеет вид:
A)
B)
C)
D)
E)
148
Общее уравнение плоскости ,проходящей
через точку
перпендикулярно вектору
имеет вид:
A)
B)
C)
D)
E)
149.
Укажите уравнение плоскости в отрезках,
если общее уравнение плоскости имеет
вид
A)
B)
C)
D)
E)
150.
Найти направляющий вектор
прямой , заданной общими уравнениями
A)
B)
C)
D)
E)
151.
Составить канонические уравнения
прямой, проходящей через точки
и
:
A)
B)
C)
D)
E)
152.
Составить параметрические уравнения
прямой, проходящей через точку
и параллельно вектору
:
A)
B)
C)
D)
E)
153.
Найти направляющий вектор
прямой ,проходящей через точки
и
:
A)
B)
C)
D)
E)
154.
Найти угол
между прямой
и плоскостью
:
A)
B)
C)
D)
E)
155.
Найти угол
между прямой
и плоскостью
:
A)
B)
C)
D)
E)
156.
Найти расстояние
от точки
до плоскости
:
A)
B)
C)
D)
E)
157.
Уравнение прямой в пространстве ,
проходящей через точки
и
имеет вид:
A)
B)
C)
