
- •Статистика Учебное пособие.
- •Содержание (часть 1)
- •Глава 1. Методология и основные понятия статистики.
- •1.2. Статистическое наблюдение.
- •1.3. Сводка и группировка статистических данных.
- •1.4. Представление статистических данных.
- •1.4.1. Статистические таблицы.
- •1.4.2. Графическое изображение статистических данных.
- •1.4.3. Решение типовых задач.
- •Глава 2. Статистические показатели.
- •2.1. Абсолютные величины.
- •2.2. Относительные величины.
- •2.3. Средние величины.
- •2.3.1. Структурные средние.
- •2.3.2. Степенные средние.
- •Глава 3. Показатели вариации.
- •3.1. Абсолютные и относительные показатели.
- •3.3. Показатели конкуренции.
- •Глава 4. Выборочное наблюдение.
- •4.1. Выборочная совокупность (выборка) и способы её отбора.
- •4.2. Оценка математического ожидания (средней величины).
- •4.3. Оценка вероятности или доли элементов генеральной совокупности, обладающих определенным признаком.
- •Глава 5. Корреляционная связь и ее анализ.
- •5.1. Корреляционно-регрессионный анализ.
- •5.1.1. Уравнение регрессии.
- •5.1.2. Коэффициент корреляции.
- •5.1.3. Оценка уравнения регрессии.
- •5.2. Непараметрические показатели связи.
- •5.2.1. Коэффициенты ранговой корреляции.
- •5.2.2. Анализ связи атрибутивных признаков.
- •5.2.3. Анализ связи альтернативных признаков.
- •Глава 6. Статистическое изучение динамики.
- •6.1.Виды рядов динамики. Средний уровень ряда динамики.
- •6.3. Выявление основной тенденции ряда динамики.
- •6.4. Сезонные колебания.
- •Глава 7. Экономические индексы.
- •7.1. Виды экономических индексов.
- •7.2. Общие индексы средних величин.
- •Глава 8. Экспертное оценивание.
- •8.1. Организация экспертизы.
- •8.2. Обработка и анализ результатов экспертизы.
- •8.2.1. Ранжирование объектов.
- •8.2.2. Оценивание по балльной шкале.
- •8.2.3. Парные сравнения.
6.3. Выявление основной тенденции ряда динамики.
Уровни ряда динамики формируются под влиянием многих факторов, каждый из которых определяет соответствующую составляющую ряда. При анализе временных рядов выделяют следующие его составляющие:
тренд - основная тенденция развития динамического ряда (долговременное его изменение);
сезонные (циклические) колебания, зависящие от времени года (например, при продаже мороженого);
остаточные или случайные колебания, определяемые несистематическими, носящими непредсказуемый характер, причинами и вызывающие колебания уровней относительно тренда;
Наиболее простым способом выделения тренда является метод укрупнения интервалов. Он может применяться только к интервальным рядам абсолютных величин.
При использовании средней переменной укрупнение интервала обычно начинают с наименьшего возможного, т.е. с интервала, объединяющего два периода. Если в этом случае тенденция развития четко не проявляется, переходят к следующему возможному интервалу, объединяющему три периода, осуществляя расчет средних для укрупненных интервалов по формулам простой средней арифметической:
 ,
,
где
 уровни
исходного ряда динамики.
уровни
исходного ряда динамики.
|
Пример 6.8. Имеются данные о выпуске продукции на предприятии по месяцам за год:
Рассчитанные суммарный и среднемесячный выпуск продукции по кварталам путем укрупнения интервалов до трех месяцев выглядят следующим образом:
Видно, что новые данные более четко выражают закономерности изменения выпуска продукции за год – увеличение из квартала в квартал. | ||||||||||||||||||||||||||||||||||
Выявление тренда может осуществляться также методом скользящей средней. Скользящая средняя – подвижная динамическая средняя, которая исчисляется по ряду при последовательном передвижении на один интервал, т.е. сначала вычисляют средний уровень из определенного числа первых по порядку уровней ряда, затем - средний уровень из такого же числа членов, начиная со второго. На практике удобнее использовать нечетный период, так как в этом случае скользящая средняя будет отнесена к середине периода скольжения. Так, скользящие средние с продолжительностью периода, равной трем, получаются следующие:

Полученные средние приписываются к соответствующему срединному интервалу – второму, третьему и т.д.
Погашение колебаний величин индивидуальных уровней ряда динамики, обеспечиваемое методом скользящей средней, называется сглаживанием динамического ряда.
Заметим, что сглаженный ряд укорачивается
по сравнению с фактическим на
 члена с одного и другого конца, где
члена с одного и другого конца, где период скользящей средней.
период скользящей средней.
|
Пример 6.9. Для данных примера 6.8 сгладить ряд, используя скользящую среднюю с периодом три. Результаты приведены в следующей таблице.
|
Рассмотренные приёмы выявления тренда
не позволяют получить аналитическую
модель (т.е. числовую характеристику
тенденции). Для этой цели используется
аналитическое
выравнивание. Суть его заключается
в замене фактических уровней теоретическими
теоретическими ,
которые рассчитаны по определенному
уравнению
,
которые рассчитаны по определенному
уравнению ,
принятому за математическую модель
тренда и где теоретические уровни
рассматриваются как функция времени
,
принятому за математическую модель
тренда и где теоретические уровни
рассматриваются как функция времени .
.
На практике выбор формы кривой
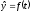 может быть основан на анализе графического
изображения уровней динамического ряда
(диаграммы рассеивания); при этом
целесообразнее воспользоваться
графическим изображением сглаженных
уровней, в которых случайные колебания
погашены. Если условия формирования
уровней ряда изменяются, то расчет
параметров выбранного уравнения не
следует вести за весь рассматриваемый
период; в этом случае необходимо разбить
исходный ряд на несколько периодов,
основываясь на оценке устойчивости
показателей динамики.
может быть основан на анализе графического
изображения уровней динамического ряда
(диаграммы рассеивания); при этом
целесообразнее воспользоваться
графическим изображением сглаженных
уровней, в которых случайные колебания
погашены. Если условия формирования
уровней ряда изменяются, то расчет
параметров выбранного уравнения не
следует вести за весь рассматриваемый
период; в этом случае необходимо разбить
исходный ряд на несколько периодов,
основываясь на оценке устойчивости
показателей динамики.
При выборе формы уравнения
 учитывают следующие рекомендации:
учитывают следующие рекомендации:
если относительно стабильны абсолютные приросты, выравнивание может быть выполнено с помощью линейной функции
 ;
;при относительно стабильных темпах роста (т.е. когда цепные коэффициенты роста примерно постоянны) используют показательную функцию
 (или её логарифм:
(или её логарифм: ,
получая при этом линейную функцию, если
уровни ряда заменить их логарифмами);
,
получая при этом линейную функцию, если
уровни ряда заменить их логарифмами);если наблюдается замедленное снижение уровней ряда, то для описания характера тренда выбирают гиперболу вида
 .
.
Рассмотрим линейную функцию
 .
Метод наименьших квадратов, исходя из
условия:
.
Метод наименьших квадратов, исходя из
условия:
 ,
(6.13)
,
(6.13)
дает систему двух нормальных уравнений
для нахождения параметров
 и
и :
:
 ,
(6.14)
,
(6.14)
где
 –
исходный уровень ряда,
–
исходный уровень ряда,
 число
членов ряда,
число
членов ряда,
 время.
время.
Если значения времени выбираются так,
чтобы
 ,
тогда получается:
,
тогда получается:
 .
(6.15)
.
(6.15)
По полученной модели для каждой даты
определяются теоретические уровни
тренда
 и стандартная ошибка аппроксимации
(или среднее квадратическое отклонение
тренда) по формуле:
и стандартная ошибка аппроксимации
(или среднее квадратическое отклонение
тренда) по формуле:
 ,
(6.16)
,
(6.16)
где
 число
параметров в уравнении тренда.
число
параметров в уравнении тренда.
Границы доверительных интервалов прогноза определяются как
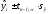 ,
(6.17)
,
(6.17)
где
 квантиль распределения Стьюдента с
квантиль распределения Стьюдента с степенями свободы при уровне значимости
степенями свободы при уровне значимости
|
Пример 6.10. Рассчитать интервальный прогноз объёма перевозок на 2007 г. с доверительной вероятностью 0,95 на основе следующих отчетных данных по грузовому автотранспортному предприятию:
Для определения формы тренда и расчета его параметров составляется вспомогательная таблица.
Первые
разности приблизительно равны между
собой, поэтому в качестве модели можно
принять уравнение прямой
Параметры
определяем по формулам (6.15):
Модель
тренда имеет вид:
Среднее
квадратическое отклонение равно
(6.16):
Точечный
прогноз на 2007 год:
Интервальный
прогноз объёма перевозок для 2007 г. при
доверительной вероятности 0,95 (уровне
значимости
|






 .
. ;
; .
. .
. .
. тыс. т.
тыс. т.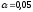 )
и числе степеней свободы 3 определяется
следующими границами (6.17):
)
и числе степеней свободы 3 определяется
следующими границами (6.17): или
или .
.