
- •Министерство образования и науки Российской Федерации
- •Глава I. Алгебра высказываний
- •§ 1. Понятие высказывания
- •§ 2. Язык исчисления высказываний
- •Примеры формул и не формул
- •§ 3. Истинностные значения формул
- •§ 4. Законы логики, противоречия, выполнимые и равносильные формулы
- •§ 5. Совершенные дизъюнктивная и конъюнктивная нормальные формы
- •§ 6. Булевы функции
- •§ 7. Логическое следование
- •§ 8. Некоторые применения алгебры высказываний
- •Глава II. Алгебра предикатов
- •§ 1. Предикаты и кванторы
- •Логические операции над предикатами
- •§ 2. Равносильные и тождественно истинные предикаты
- •§ 3. Язык исчисления предикатов
- •§ 4. Интерпретации формул исчисления предикатов
- •§ 5. Приведённая и предварённая нормальные формы
- •§ 6. О структуре современных математических теорий
- •§ 7. Виды математических утверждений
- •§ 8. Некоторые методы доказательства теорем
- •Глава III. Формальные аксиоматические теории
- •§ 1. Формальные и неформальные аксиоматические теории
- •Примеры формальных аксиоматических теорий
- •Примеры доказательств в формальном исчислении высказываний
- •(В): (введение квантора ), (в): (введение квантора ),
- •Примеры доказательств в формальном исчислении предикатов
- •Аксиомы равенства:
- •Аксиомы операций сложения и умножения:
- •Примеры теорем формальной арифметики
- •§ 2. Непротиворечивость аксиоматических теорий
- •§ 3. Полнота аксиоматических теорий
- •§ 4. Разрешимость аксиоматических теорий
- •§ 5. Независимость системы аксиом теории
- •§ 6. Формальное исчисление высказываний
- •Приложение: формальная теория множеств
- •§ 1. Азы наивной теории множеств
- •Основные операции над множествами
- •§ 2. Аксиоматика Цермело-Френкеля теории множеств
- •40. Аксиома существования булеана (множества всех подмножеств) :
- •50. Аксиома (неупорядоченной) пары :
- •§ 3. Формальная теория множеств: райские кущи или адские дебри ?
- •А) основная литература:
- •Б) дополнительная литература:
- •Список основных обозначений
- •Предметный указатель
- •Алексей Игоревич Валицкас
§ 5. Приведённая и предварённая нормальные формы
По аналогии с исчислением высказываний, найдём некоторую нормальную форму, к которой можно равносильными преобразованиями привести любую формулу исчисления предикатов.
С помощью известных
основных равносильностей (A
B)
(![]()
B)
и
(A
B)
((A
B)
(
B)
и
(A
B)
((A
B)
(![]()
![]() ))в произвольной
формуле исчисления предикатов можно
избавиться от всех логических связок
и
. Затем, по
законам де Моргана
))в произвольной
формуле исчисления предикатов можно
избавиться от всех логических связок
и
. Затем, по
законам де Моргана
![]() ,
правилу двойного отрицания
,
правилу двойного отрицания
![]()
A
и равносильностям
с кванторами
A
и равносильностям
с кванторами
![]()
(
x
(
x
![]() (x,
y)),
(x,
y)),
![]()
(
x
(
x
![]() (x,
y))
можно
переработать все “длинные” отрицания
(т.е. отрицания, стоящие над формулами,
не являющимися пропозициональными
переменными и предикатными символами)
в “короткие”, добившись, чтобы отрицания
стояли только над пропозициональными
переменными или над предикатными
символами.
(x,
y))
можно
переработать все “длинные” отрицания
(т.е. отрицания, стоящие над формулами,
не являющимися пропозициональными
переменными и предикатными символами)
в “короткие”, добившись, чтобы отрицания
стояли только над пропозициональными
переменными или над предикатными
символами.
Полученный вид формулы называется приведённым или приведённой формой (ПФ) . Таким образом, доказана следующая
Теорема (о ПФ). Любая формула исчисления предикатов равносильна некоторой приведённой форме.
Примеры:
1.
(
x (
y (P(y)
Q(x))))
(
x (
y (![]() (y)
Q(x)))) – ПФ.
(y)
Q(x)))) – ПФ.
2.
![]() )
)
(
y ((
x P(x))
![]() (x,
y))) – ПФ.
(x,
y))) – ПФ.
3.
![]()
![]()
![]() –ПФ.
–ПФ.
Говорят, что формула исчисления предикатов находится в предварённой нормальной форме (ПНФ), если она либо не содержит кванторов, либо имеет следующий вид: Q1 x1 (Q2 x2 (… (Qn xn Ф(x1 , … , xn )))…), где Qi – один из кванторов или (1 i n), формула Ф бескванторная и может зависеть от других переменных, кроме x1 , … , xn . Иными словами, кванторы в ПНФ предшествуют её бескванторной подформуле Ф и область действия каждого квантора распространяется до конца формулы (не учитывая закрывающие скобки).
Если формула является ПНФ и приведена, то говорят, что она находится в предварённой приведённой нормальной форме (ППНФ) .
Примеры: 1. (P(x) Q(y)) – бескванторная формула в ПНФ и ППНФ.
2. ( x ( y (P(y) Q(x)))) – ПНФ, но не ППНФ.
3. ( x (( y P(y)) Q(x))) – не ПНФ, т.к. область действия квантора распространяется только на P(x), а не до конца формулы.
4. (P(z, y) ( x Q(x))) – не ПНФ, т.к. квантор не предшествует подформуле P(z, y).
Теорема (о ППНФ). Любая формула исчисления предикатов равносильна некоторой предварённой приведённой нормальной форме.
Доказательство. Будем исследовать формулы в процессе их создания по правилам образования формул (Ф1)-(Ф5) и приводить их к ППНФ.
Во-первых, любая бескванторная формула сама находится в ПНФ и равносильна некоторой приведённой форме ввиду предыдущей теоремы. Таким образом, любая формула, возникшая по правилам (Ф1), (Ф2), обладает ППНФ.
Во-вторых, если для формул A и B уже найдены равносильные им ППНФ:
A Q1 x1 (Q2 x2 (… (Qn xn C(x1 , … , xn ))…)),
B R1 y1 (R2 y2 (… (Rm ym D(y1 , … , ym ))…)) = ,
где Qi
, Rj
– один из
кванторов
или
(1
i
n,
1
j
m),
то (как уже отмечалось выше) связанные
переменные в этих формулах можно
переобозначить уникальными буквами
так, чтобы в формуле для А
не было
одинаковых связанных переменных с
формулой для B
и чтобы все
связанные переменные отличались от
свободных.
Найдём ППНФ,
равносильную формулам
![]() ,
(A
B),
(A
B),
(A
B),
(A
B).
,
(A
B),
(A
B),
(A
B),
(A
B).
Для
![]() воспользуемся равносильностями(2),
теоремы об основных равносильностях
с кванторами:
воспользуемся равносильностями(2),
теоремы об основных равносильностях
с кванторами:
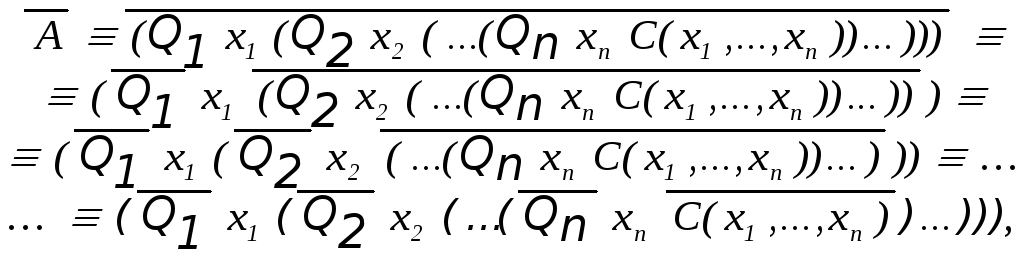
где
![]() –
кванторы,
противоположные кванторам Qi
(1
i
n).
Последняя формула в этой цепочке – ПНФ
– является искомой. Остаётся привести
её к приведённому виду, избавившись от
“длинных” отрицаний в бескванторной
формуле. Таким образом,
–
кванторы,
противоположные кванторам Qi
(1
i
n).
Последняя формула в этой цепочке – ПНФ
– является искомой. Остаётся привести
её к приведённому виду, избавившись от
“длинных” отрицаний в бескванторной
формуле. Таким образом,
![]() обладает равносильнойППНФ.
обладает равносильнойППНФ.
Для остальных формул вида (A B), где { , } рассуждения однотипны и используют равносильности (5), (6) теоремы об основных равносильностях с кванторами (следует учесть, что все связанные переменные уникальны, так что условия для применения равносильностей (5), (6) выполнены): (А B)
((Q1 x1 (…(Qn xn С(x1 , … , xn ))…)) (R1 y1 (…(Rm ym D(y1 , … , ym ))…))) =
= ((Q1 x1 (Q2 x2 (… (Qn xn С)…))) ) (Q1 x1 ((Q2 x2 (… (Qn xn С))…)) ))
(Q1 x1 (Q2 x2 ((… (Qn xn С)…)) ))) …
… (Q1 x1 (Q2 x2 (…(Qn xn (С ))…))) (Q1 x1 (Q2 x2 (…(Qn xn ( С))…)))
(Q1 x1 (Q2 x2 (… (Qn xn ((R1 y1 (R2 y2 (… (Rm ym D)…))) С))…)))
(Q1 x1 (Q2 x2 (… (Qn xn (R1 y1 ((R2 y2 (… (Rm ym D)…)) С)))…)))
(Q1 x1 (Q2 x2 (… (Qn xn (R1 y1 (R2 y2 ((… (Rm ym D)…) С))))…))) …
… (Q1 x1 (Q2 x2 (…(Qn xn (R1 y1 (R2 y2 (…(Rm ym (D С))…))))…))),
и последняя формула является ППНФ.
Связки
и
выражаются
через
,
,
![]() ,
так что для формул вида(A
B)
и (A
B)
существование
ППНФ следует
из предыдущего.
,
так что для формул вида(A
B)
и (A
B)
существование
ППНФ следует
из предыдущего.
Таким образом, все формулы, полученные по правилу (Ф3) образования формул, обладают ППНФ.
Наконец, если A(x) – формула со свободной переменной x, которая уже равносильна некоторой ППНФ:
A(x) (Q1 x1 (Q2 x2 (… (Qn xn C(x, x1 , … , xn ))…))),
где Qi (1 i n) – один из кванторов или , то формула (Q x A(x)), очевидно, равносильна формуле (Q x (Q1 x1 (Q2 x2 (… (Qn xn C(x, x1 , … , xn ))…)))) – ППНФ. Таким образом, любая формула обладает равносильной ППНФ.
Теорема доказана.
Примеры: 1.
(
x ((
y P(y))
Q(y, x)))
(
x (![]()
Q(y, x)))
Q(y, x)))
(
x ((
y
![]() (y))
Q(y, x)))
(
x ((
z
(y))
Q(y, x)))
(
x ((
z
![]() (z))
Q(y, x)))
(z))
Q(y, x)))
(
x (
z (![]() (z)
Q(y, x)))) – ППНФ.
(z)
Q(y, x)))) – ППНФ.
2. (P(u, y) ( y Q(y))) (P(u, y) ( z Q(z)))
(( z Q(z)) P(u, y)) ( z (Q(z) P(u, y))) – ППНФ.
3.
((
x R(x, y, z))
![]() )
((
x R(x, y, z))
(
x
)
((
x R(x, y, z))
(
x
![]() (x,
y)))
(x,
y)))
(![]()
(
t
(
t
![]() (t,
y)))
((
x
(t,
y)))
((
x
![]() (x,
y, z))
(
t
(x,
y, z))
(
t
![]() (t,
y)))
(t,
y)))
(
x (![]() (x,
y, z)
(
t
(x,
y, z)
(
t
![]() (t,
y))))
(
x (
t (
(t,
y))))
(
x (
t (![]() (x,
y, z)
(x,
y, z)
![]() (t,
y)))) – ППНФ.
(t,
y)))) – ППНФ.
4.
((
x P(x, y))
((
x P(x, x))
(
z
![]() )))
)))
((
x P(x, y))
((
x P(x, x))
(
z
![]() )))
)))
((
x P(x, y))
((
x P(x, x))
(
z (Q(y, z)
![]() ))))
))))
((
x P(x, y))
((
x P(x, x))
(
z (Q(y, z)
(
x
![]() (x,
z))))))
(x,
z))))))
((
x P(x, y))
((
u P(u, u))
(
z (Q(y, z)
(
v
![]() (v,
z))))))
(v,
z))))))
((
x P(x, y))
((
u P(u, u))
(
z (
v (Q(y, z)
![]() (v,
z))))))
(v,
z))))))
((
x P(x, y))
((
u
![]() (u,
u))
(
z (
v (Q(y, z)
(u,
u))
(
z (
v (Q(y, z)
![]() (v,
z))))))
(v,
z))))))
((
x P(x, y))
(
z ((
u
![]() (u,
u))
(
v (Q(y, z)
(u,
u))
(
v (Q(y, z)
![]() (v,
z))))))
(v,
z))))))
((
x P(x, y))
(
z (
v ((
u
![]() (u,
u))
(Q(y, z)
(u,
u))
(Q(y, z)
![]() (v,
z))))))
(v,
z))))))
((
x P(x, y))
(
z (
v (
u (![]() (u,
u)
(Q(y, z)
(u,
u)
(Q(y, z)
![]() (v,
z)))))))
(v,
z)))))))
(
z ((
x P(x, y))
(
v (
u (![]() (u,
u)
(Q(y, z)
(u,
u)
(Q(y, z)
![]() (v,
z)))))))
(v,
z)))))))
(
z (
v ((
x P(x, y))
(
u (![]() (u,
u)
(Q(y, z)
(u,
u)
(Q(y, z)
![]() (v,
z)))))))
(v,
z)))))))
(
z (
v (
u ((
x P(x, y))
(![]() (u,
u)
(Q(y, z)
(u,
u)
(Q(y, z)
![]() (v,
z)))))))
(v,
z)))))))
( z ( v ( u ( x (P(x, y) (
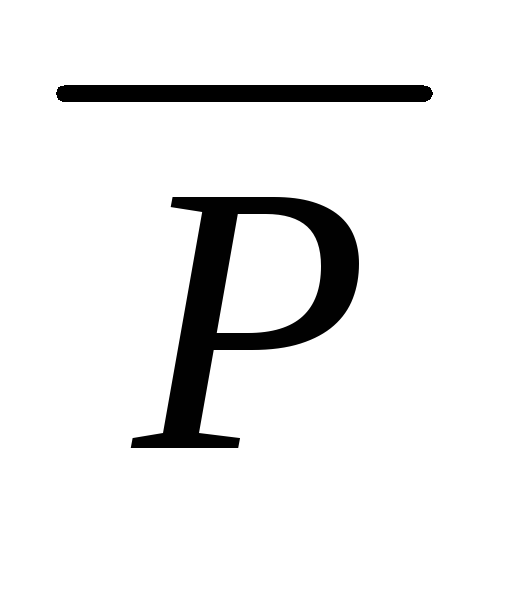 (u,
u)
(Q(y, z)
(u,
u)
(Q(y, z)
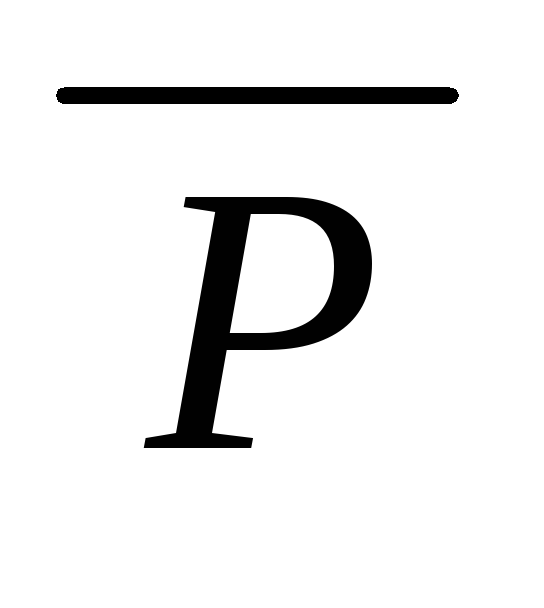 (v,
z))))))))
– ППНФ.
(v,
z))))))))
– ППНФ.
