§ 2. Равносильные и тождественно истинные предикаты

Два предиката P(x₁ , … , x_n ) и Q(x₁ , … , x_n ), определённые на множестве А (т.е. предикаты с условиями Aⁿ  D(P)  D(Q)), называют равносильными на множестве А и пишут при этом P(x₁ , … , x_n ) _А Q(x₁ , … , x_n ), если выполнено равенство D₁(P)  Aⁿ = D₁(Q)  Aⁿ , другими словами, если  a₁ , … , a_n  A (P(a₁ , … , a_n ) = 1  Q(a₁ , … , a_n ) = 1). Если D(P) = Aⁿ = D(Q), то вместо P(x₁ , … , x_n ) _А Q(x₁ , … , x_n ) будем кратко писать P(x₁ , … , x_n )  Q(x₁ , … , x_n ).

Если Aⁿ  D₁(P), т.е.  a₁ , … , a_n  A P(a₁ , … , a_n ) = 1, то предикат P(x₁ , … , x_n ) называется тождественно истинным на множестве A : P(x₁ , … , x_n ) _А 1. Аналогично, предикат P(x₁ , … , x_n ) называют тождественно ложным на множестве A: P(x₁ , … , x_n ) _А 0, если Aⁿ  D₀(P), т.е. выполнено условие  a₁ , … , a_n  A P(a₁ , … , a_n ) = 0 .

Примеры: 1. Равносильны ли предикаты P(x) = “> 1”и Q(x) = “x < 1” на множестве R₊ = {r  R | r > 0} = (0; +∞) ?

Во-первых, оба предиката определены на R₊ : D(P) = R \ {0}, D(Q) = R . Найдём их области истинности. Для предиката Q ясно, что D₁(Q) = (–∞; 1). Для предиката P имеем: > 1 > 0 x(1–x) > 0  x  (0; 1). Хотя получили, что D₁(P)  D₁(Q), но

D₁(P)  R₊ = (0; 1)  (0; +∞) = (0; 1) = (–∞; 1)  (0; +∞) = D₁(Q)  R₊ ,

так что P(x) Q(x).

2. Рассмотренные выше предикаты P(x) и Q(x) не равносильны на множестве A = R \ {0}: D₁(P)  A = (0; 1)  (–∞; 1) \ {0} = D₁(Q)  A .

3. Предикат Q(x) тождественно истинен на R_– = {r  R | r < 0} = (–∞; 0).

Действительно, R_–  D₁(Q) = (–∞; 1).

4. Предикат P(x) тождественно ложен на множестве (1; +∞).

5. Предикаты P(x, y) = “xy  Z” и Q(x, y) = “x  Z  y  Z” равносильны на множестве A = Z, но не равносильны на множестве R.

В самом деле, оба предиката определены на R, точнее D(P) = RR = D(Q), и тождественно истинны на Z : высказывания  a, b  Z ab  Z и  a, b  Z (a  Z)  (b  Z) оба истинны. Поэтому P(x) _Z Q(x). С другой стороны, D₁(Q) = ZZ  D₁(P): например, (0,5; 2)  D₁(P) \ ZZ .

Упражнения: 1. Докажите, что P(x) _А Q(x), где A = (0; 10), P(x) = “x > 0,5”, Q(x) = “x² > 0,5x”.

2. Равносильны ли на R₊ , R предикаты из предыдущего упражнения ?

3. Верно ли, что P(x₁ , … , x_n ) _А Q(x₁ , … , x_n ) тогда и только тогда, когда (P  Q) _A 1 ? А если (P  Q) _A 1 ?

4. Равносильны ли предикаты P(x, y) = “xy = 1” и Q(x, y) = “x = 1 / y” на множествах R, R \ {0}, N ?

Приведём некоторые основные равносильности предикатов с кванторами.

Теорема (об основных равносильностях с кванторами).

(0)  x  A P(x, y)   z  A P(z, y),  x  A P(x, y)   z  A P(z, y), где P(x, y) не зависит от z,

1.  x  A ( y  A P(x, y, z))   y  A ( x  A P(x, y, z)),

 x  A ( y  A P(x, y, z))   y  A ( x  A P(x, y, z))

(для разноимённых кванторов утверждения не верны),

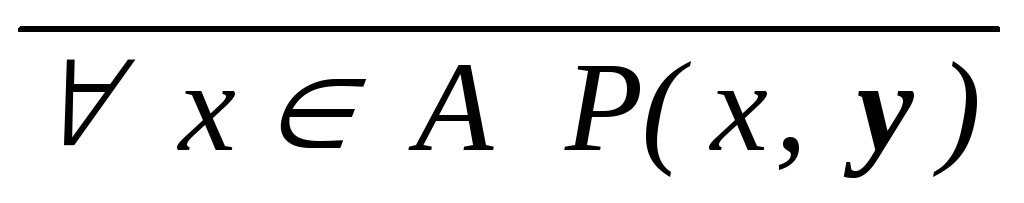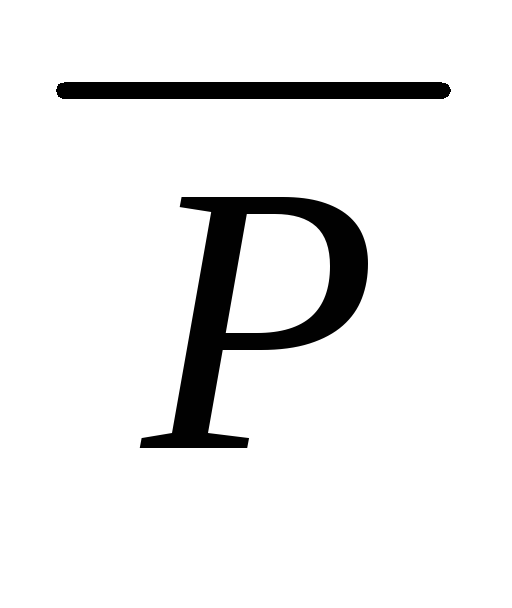2.  x  A (x,y),  x  A P(x, y)  ,

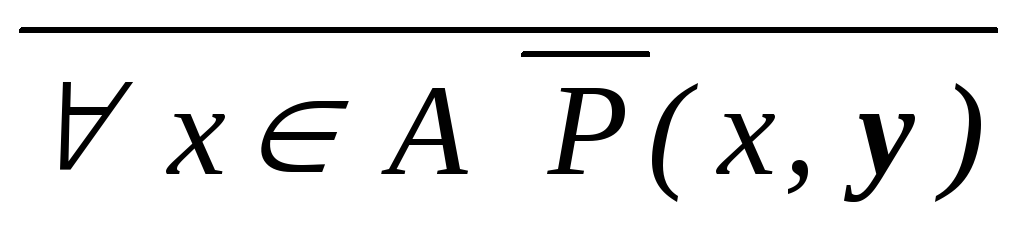 x  A (x,y),  x  A P(x, y)  ,

3. ( x  A P(x, y))  ( x  A Q(x, y))   x  A (P(x, y)  Q(x, y))

(для связки  утверждение не верно),

4. ( x  A P(x, y))  ( x  A Q(x, y))   x  A (P(x, y)  Q(x, y))

(для связки  утверждение не верно),

5. ( x  А Р(х, y))  R(y)   x  A (P(x, y)  R(y)),

( x  А Р(х, y))  R(y)   x  A (P(x, y)  R(y)),

6. ( x  А Р(х, y))  R(y)  ( x  А (Р(x, y)  R(y)),

( x  А Р(х, y))  R(y)  ( x  А (Р(x, y)  R(y)),

7.  х  А (R(y) Р(х, y))  R(y) ( x  А Р(х, y)),

 х  А (R(y)  Р(х, y))  R(y)  ( x  А Р(х, y))

8. ( x  А Р(х, y))  R(y)  ( x  А (Р(x, y)  R(y)),

( x  А Р(х, y))  R(y)  ( x  А (Р(x, y)  R(y))

(всюду жирные буквы обозначают, вообще говоря, наборы переменных, которые могут и отсутствовать, в равносильностях (5)–(8) предикат R(y) не зависит от x).

Доказательство. Все равносильности доказываются единообразно, исходя из определений истинностных значений предикатов с кванторами и равносильности предикатов.

(0) Области истинности обоих предикатов  x  A P(x, y) и  z  A P(z, y) состоят из тех наборов а = (a₁ ; … ; a_n)  Aⁿ, при которых найдётся элемент b  A со свойством P(b, a) = 1, а значит, эти области истинности совпадают.

(1) Область истинности предиката  x  A ( y  A P(x, y, z)) состоит из всех наборов а = (a₁ ; … ; a_n)  Aⁿ , при которых предикат  y  A P(c, y, a) имеет значение 1 при любом с  A, т.е. из всех наборов а  Aⁿ со свойством P(c, d, a) = 1 при любых c, d  A.

Точно так же область истинности предиката  y  A ( x  A P(x, y, z)) состоит из всех наборов а = (a₁ ; … ; a_n)  Aⁿ , при которых предикат  x  A P(x, d, a) принимает значение 1 при любом d  A, т.е. из тех наборов а  Aⁿ, при которых P(c, d, a) = 1 при любых c, d  A.

Сравнение выводов, сделанных в предыдущих абзацах, доказывает (1).

(2) Область истинности предиката состоит из всех таких наборов а = (a₁ ; … ; a_n)  Aⁿ , для которых предикат  x  A P(x, a) принимает значение 0, т.е. из всех таких наборов а  Aⁿ, при которых P(c, a) = 0 при любом c  A. Но множество всех таких наборов образует и множество истинности предиката  x  A (x, y), что и доказывает равносильность рассматриваемых предикатов.

(3) Область истинности предиката ( x  A P(x, y))  ( x  A Q(x, y)) состоит из всех наборов а = (a₁ ; … ; a_n)  Aⁿ, при которых ( x  A P(x, a)) = 1 = = ( x  A Q(x, a)), т.е. из всех a  Aⁿ, для которых P(c, a) = 1 = Q(c, a) при любом c  A. Это множество наборов совпадает с множеством истинности исследуемого предиката  x  A (P(x, y)  Q(x, y)).

(5) Область истинности предиката ( x  А Р(х, y))  R(y) состоит из множества всех таких а = (a₁ ; … ; a_n)  Aⁿ , для которых либо R(a) = 1, либо P(c, a) = 1 при любом с  A. По определению дизъюнкции, это значит, что (P(c, a)  R(a)) = 1 при любом c  A, т.е. множество рассматриваемых наборов a  Aⁿ совпадает с областью истинности предиката  x  A (P(x, y)  R(y)).

(6) Область истинности предиката ( x  А Р(х, y))  R(y) состоит из множества всех таких а = (a₁ ; … ; a_n)  Aⁿ , для которых P(c, a) = 1 при некотором с  A и R(a) = 1. Это значит, что (Р(с, a)  R(a)) = 1, т.е. мнжество рассматриваемых наборов a  Aⁿ совпадает с областью истинности предиката  x  А (Р(x, y)  R(y)).

(7) ( х  А (R(y)  Р(х, y)))  ( x  A ((y) P(x, y))) 

 ( x  A (P(x, y)  (y))) (( x  А Р(х, y))  (y)) 

 ((y)  ( x  А Р(х, y)))  (R(y)  ( x  А Р(х, y))).

(8) (( x  А Р(х, y))  R(y))  (( x  A (x,y))  R(y))

( x  A ((x,y)  R(y)))  ( x  А (Р(x, y)  R(y))).

Теорема доказана.

Замечание: Утверждения пункта (0) доказанной теоремы носят общематематический характер: не важно как обозначать связанную переменную. Так, результат суммирования не зависит от обозначения индекса суммирования, а интеграл – от переменной интегрирования.

Приведём примеры, показывающие существенность ограничений в доказанной теореме:

Примеры: 1.  x  R ( y  R x > y)  y  R ( x  R x > y), т.к. левая часть истинна, а правая – ложна.

2. ( x  R x > 0)  ( x  R x  0)  x  R (x > 0)  (x  0), т.к. левая часть ложна, а правая – истинна.

3. ( x  R x > 0)  ( x  R x  0)  x  R (x > 0)  (x  0), т.к. левая часть истинна, а правая – ложна.

4. Следующие равносильности не верны:

 х  А (Р(х)  R) ( x  А Р(х))  R,

 х  А (Р(х)  R) ( x  А Р(х))  R,

 х  А (Р(х)  R) ( x  А Р(х))  R,

 х  А (Р(х)  R) ( x  А Р(х))  R.

Действительно, пусть R  0, P(x) = “x = 0”, A = R. Тогда P(x)  R  “x  0”, и

 х  А (Р(х)  R)   x  R (x  0) – ложно, а ( x  А Р(х))  R     x  R x  0 – истинно.

 х  А (Р(х) R)   х  R (х  0) – истинно, а ( x  А Р(х)) R     x  R x  0 – ложно.

 х  А (Р(х)  R)   х  R (x  0) – ложно, а ( x  А Р(х))  R     x  R x  0 – истинно.

 х  А (Р(х)  R)   х  R (х  0) – истинно, а ( x  А Р(х))  R     x  R x  0 – ложно.

Таким образом, при преобразовании формул нужно осторожно обращаться с кванторами там, где стоят логические связки импликации и эквивалентности.

5. Если предикат R зависит от x, то равносильности (5)–(8) могут быть не верны. Например,

( x  R (х < y))  (x = y)  (x = y) 0   x  R ((x < y)  (x = y)),

( x  N (х < 1))  (x = 1)  (x = 1) 1   x  N ((x < 1)  (x = 1)).

Примеры существенности условий теоремы для равносильностей (6)–(8) приведите самостоятельно.