
- •IIсеместр
- •Содержание.
- •1. Требования к оформлению типового расчёта
- •Типовой расчёт №1
- •Задание №5.
- •Задание №6.
- •Задание №7
- •Задание №8.
- •Задание №14.
- •Задание №15.
- •Задание №16.
- •Задание №17.
- •Задание №18.
- •Задание №23.
- •Задание №24.
- •Задание №25.
- •Задание №26.
- •Задание №27.
- •Задание №28.
- •3. Примерный список рекомендуемой литературы
- •Гмурман в.Е. Руководство к решению задач по теории вероятностей и математической статистике. – м.: Высшая школа, 2004.
Задание №7
Вычислить:
7.1. 2A+BC,
еслиA=
![]() ;B=
;B=
![]() ;
С =
;
С =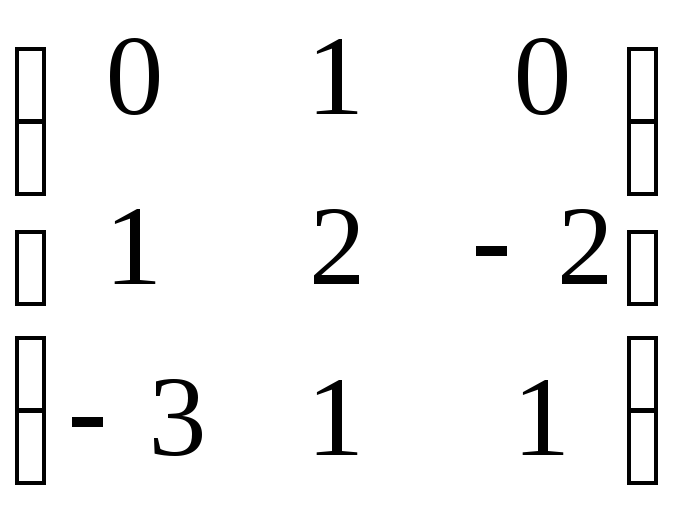 .
.
7.2. 3A – BC, если
A =
![]() ;
B =
;
B =![]() ;
С =
;
С = 
7.3. BC – 4A, если
A =
![]() ;
B =
;
B =![]() ;
С =
;
С =
 .
.
7.4. 5A +BC, если A
=
![]() ;
B =
;
B =![]() ;
С =
;
С =
 .
.
7.5. 2AB + C, если A
=
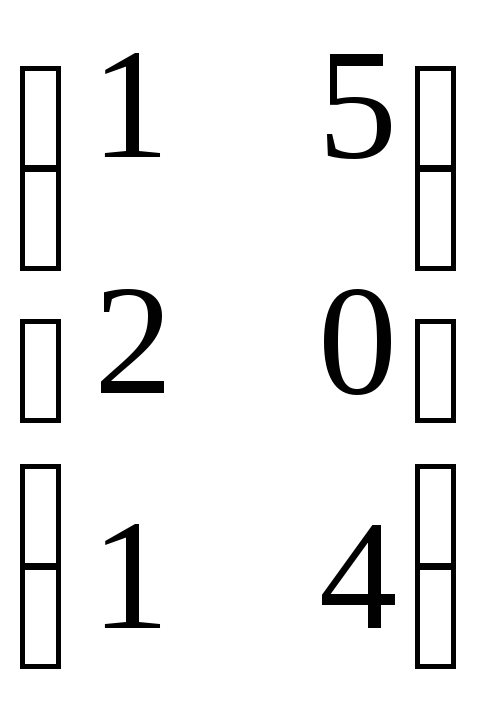 ;
B =
;
B =![]() ;
C =
;
C =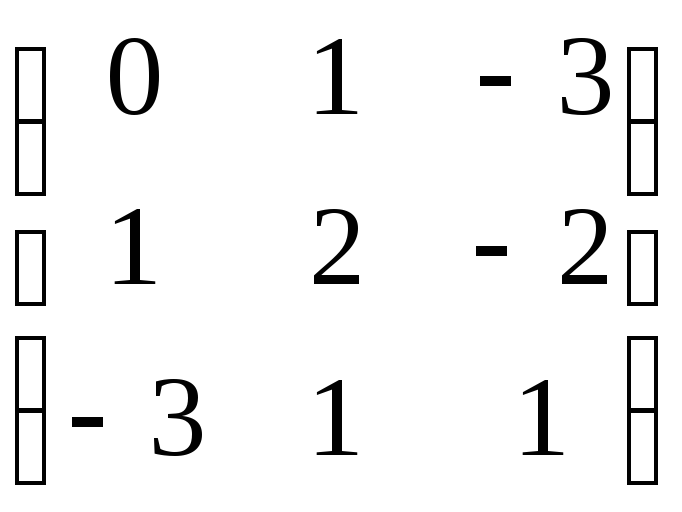 .
.
7.6. AB + 3C, если
A =
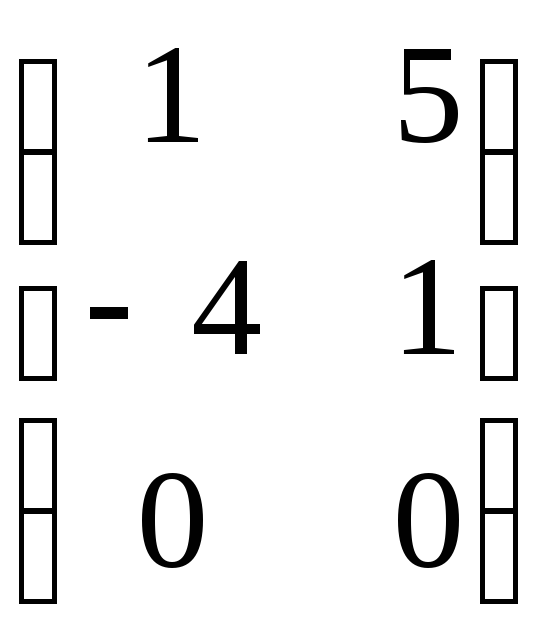 ; B =
; B =![]() ; C =
; C =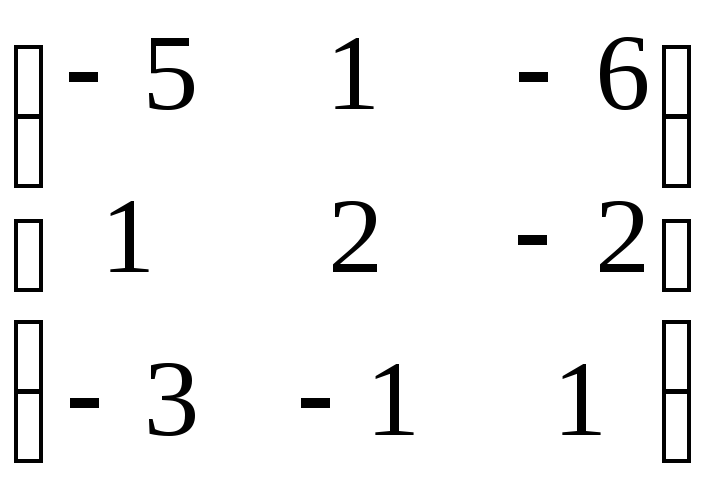 .
.
7.7. AB– 4C,
еслиA=
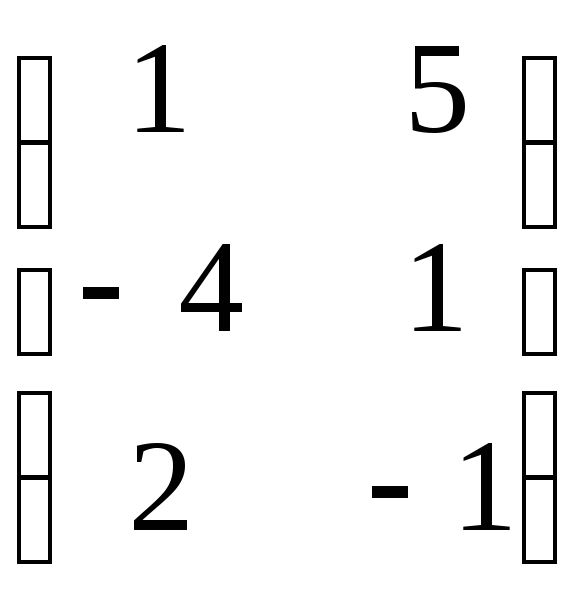 ;B=
;B=
![]() ; С =
; С =
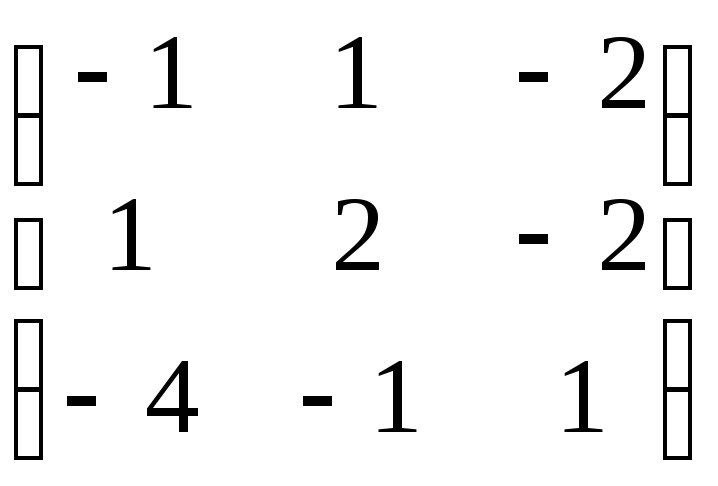 .
.
7.8. AВ + 5C,
еслиA=
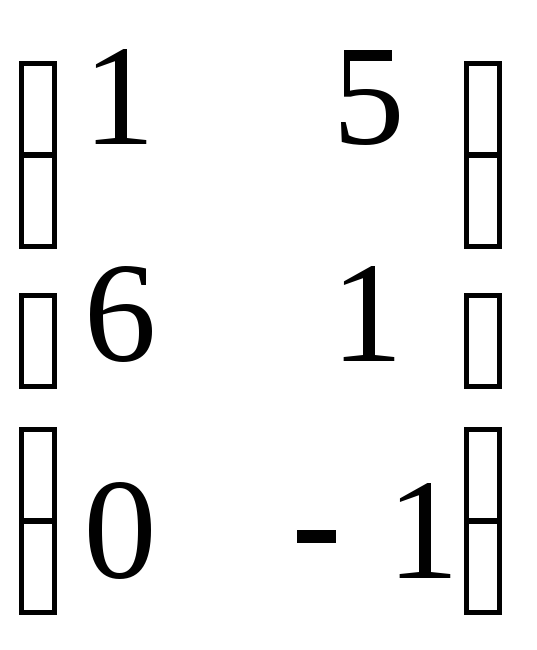 ;B=
;B=
![]() ;C=
;C=
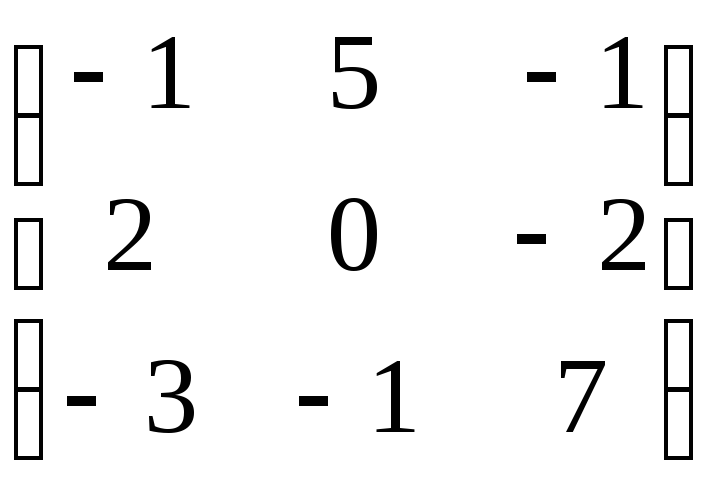 .
.
7.9. AB+ 3C,
еслиA=
![]() ;B=
;B=
![]() ; С =
; С =
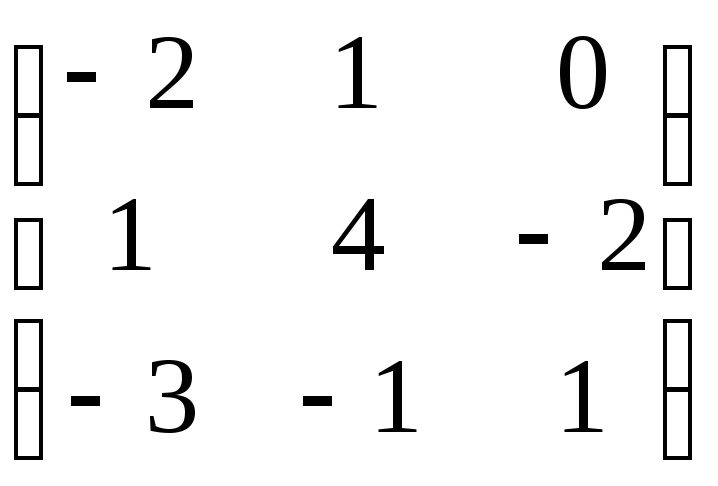 .
.
7.10. AB + 2C, если
A =
![]() ; B =
; B =![]() ; C =
; C = .
.
7.11. AB – 4C, если
A =
![]() ; B =
; B =![]() ; C =
; C =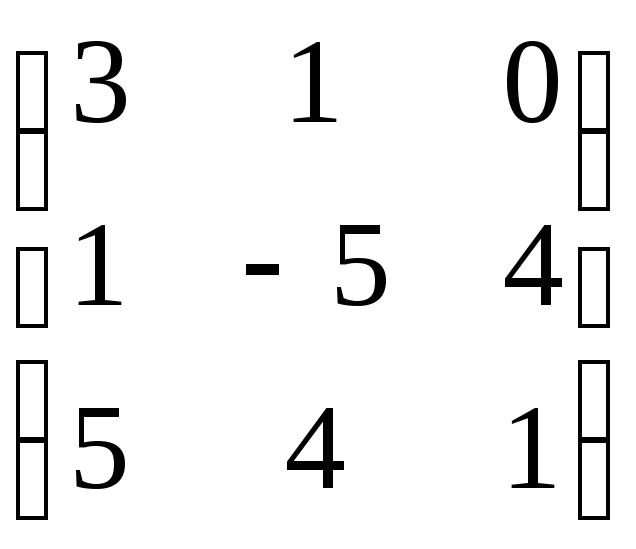 .
.
7.12. AB– 3C,
еслиA=
![]() ;B=
;B=
![]() ; С =
; С =
 .
.
7.13. 3A + BC, если
A =
![]() ; B =
; B =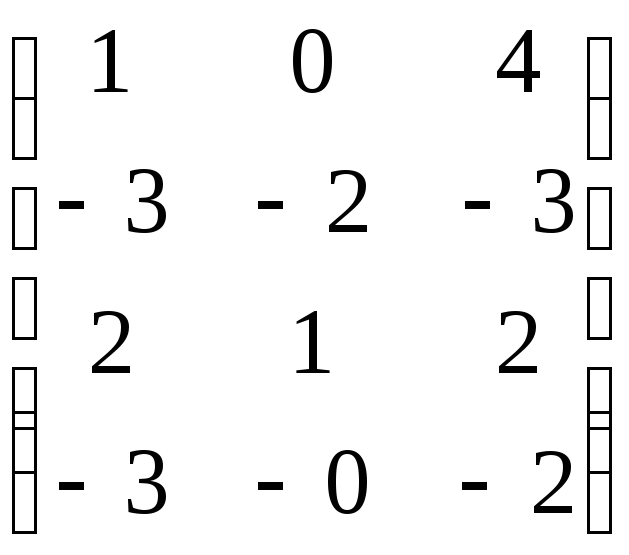 ; C =
; C =![]() .
.
7.14. 4A –BC, если
A =
![]() ; B =
; B =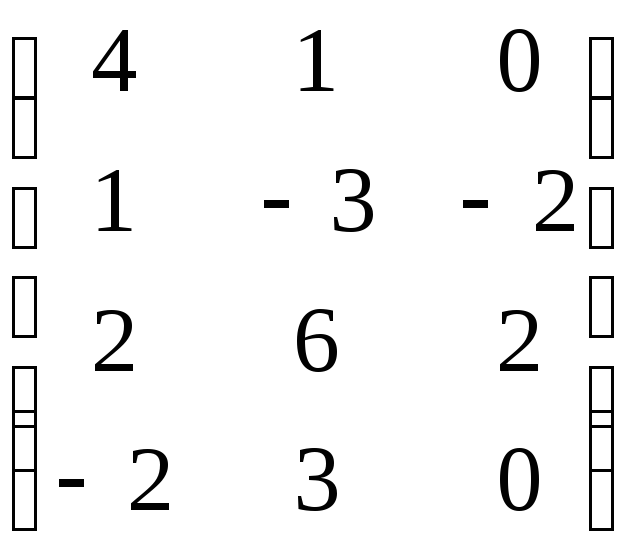 ; С =
; С =
![]() .
.
7.15. A + 2BC, если
A =
![]() ; B =
; B = ; С =
; С =
![]() .
.
7.16. A – 2BC, если
A =
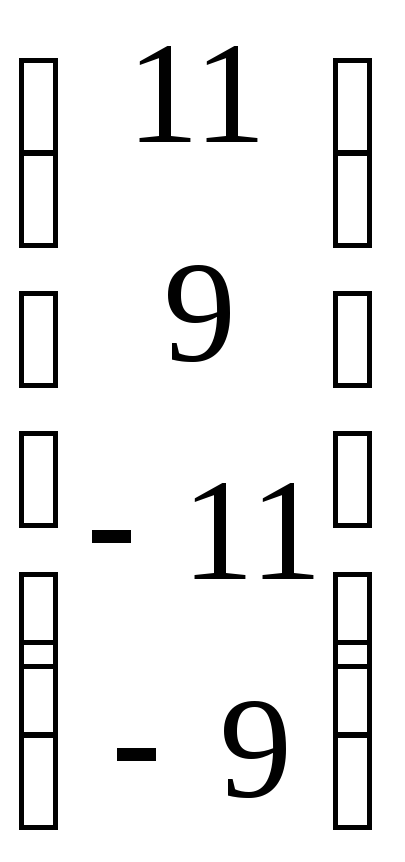 ; B =
; B = ; С =
; С =
![]()
7.17. 2A + BC, если
A =
![]() ; B =
; B =![]() ; С =
; С =
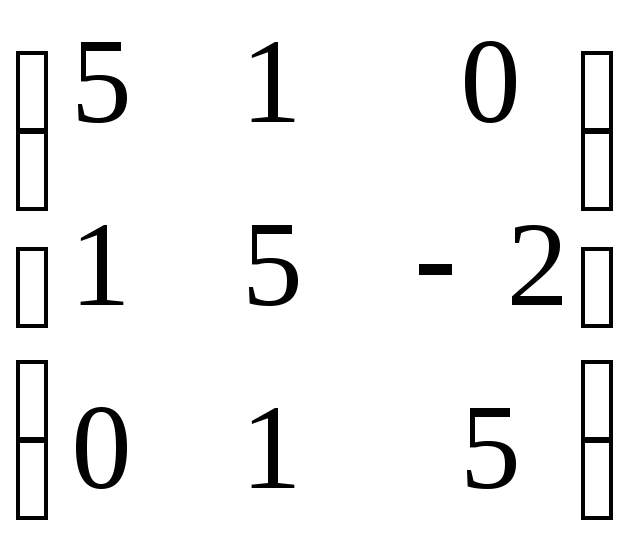 .
.
7.18. 3A – BC, если
A =
![]() ; B =
; B =![]() ; С =
; С =
 .
.
7.19. BC – 4A, если
A =
![]() ; B =
; B =![]() ; С =
; С =

7.20. 5A + BC, если
A =
![]() ; B =
; B =![]() ; C =
; C =
7.21. 2AB + C, если
A =
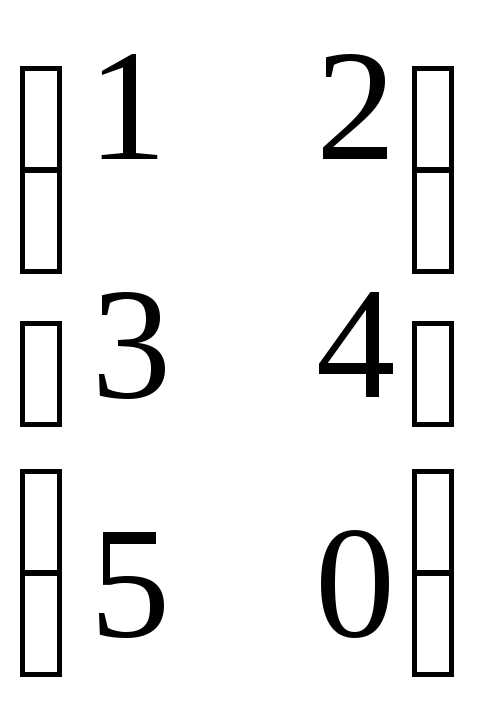 ; B =
; B =![]() ; C =
; C =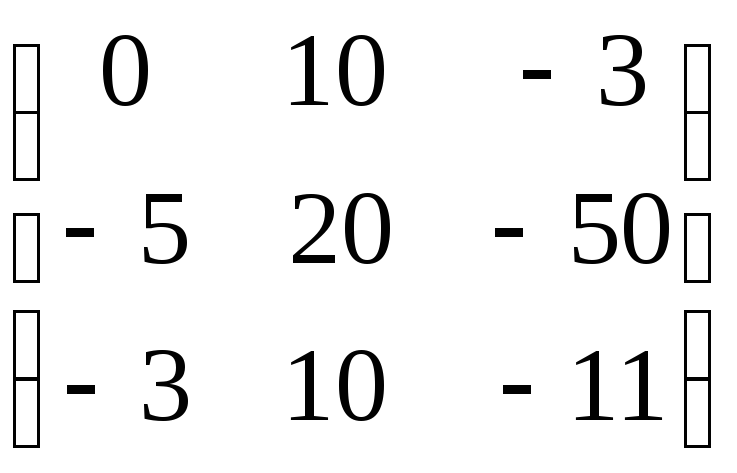 .
.
7.22. AB + 3C, если
A =
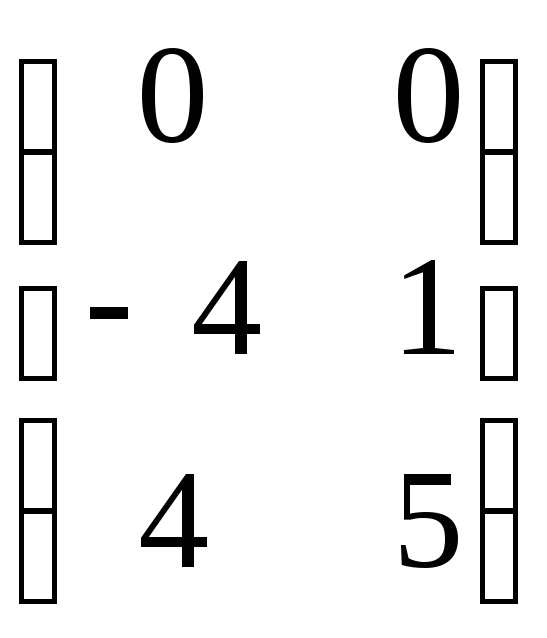 ; B =
; B =![]() ; C =
; C =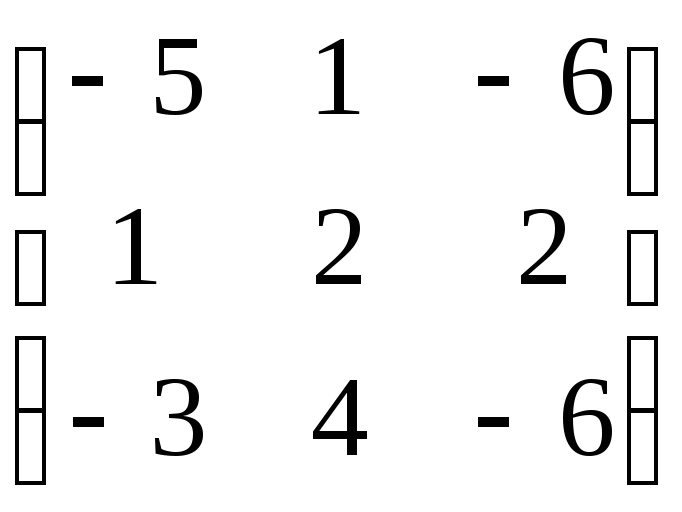 .
.
7.23. AB – 4C, если
A =
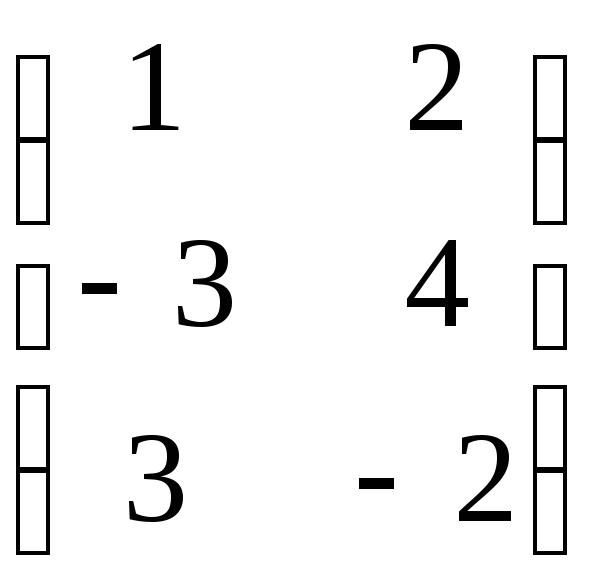 ; B =
; B =![]() ; C =
; C = .
.
7.24. AB + 5C, если
A =
 ; B =
; B =![]() ; C =
; C =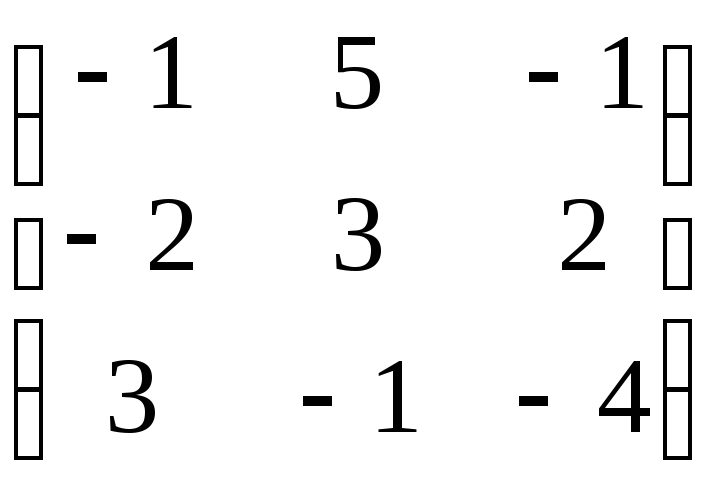 .
.
7.25. AB +3C, если A
=
![]() ; B =
; B =![]() ; C =
; C =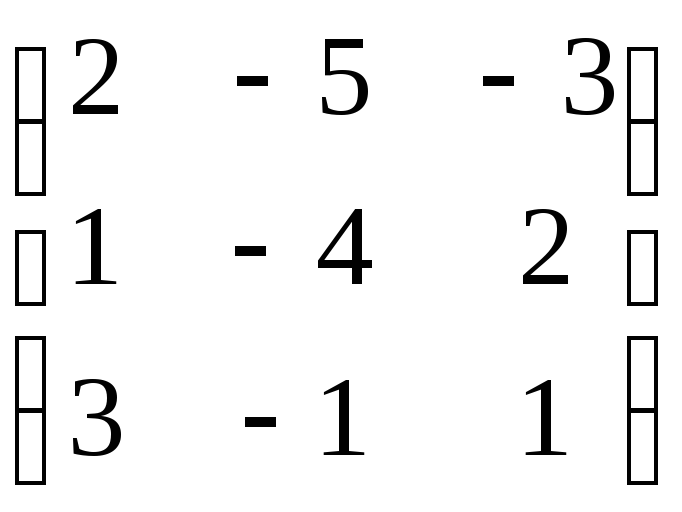 .
.
7.26. AВ + 2C, если
A =
![]() ; B =
; B =![]() ; C =
; C =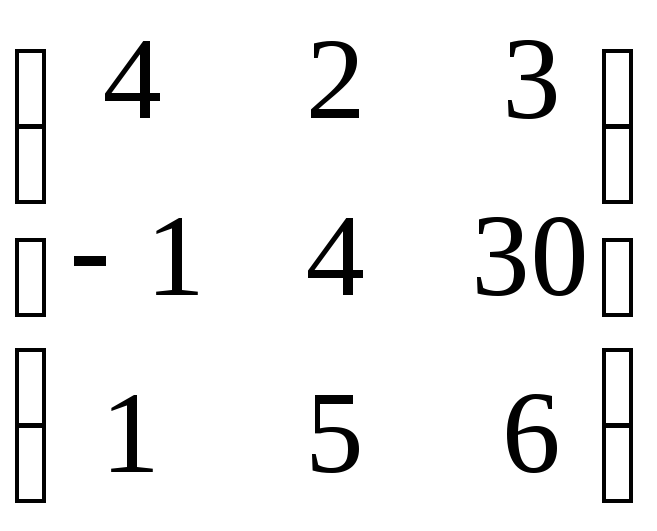 .
.
7.27. AB – 4C, если
A =
![]() ; B =
; B =![]() ; C =
; C =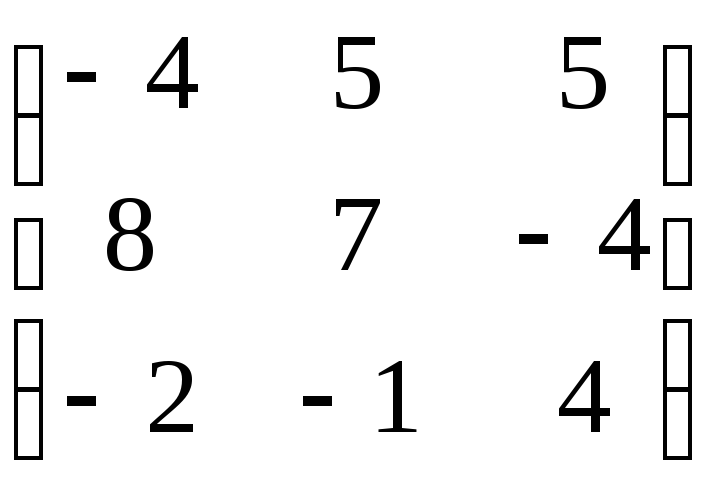 .
.
7.28. AB – 3C, если
A =
![]() ; B =
; B =![]() ; C =
; C =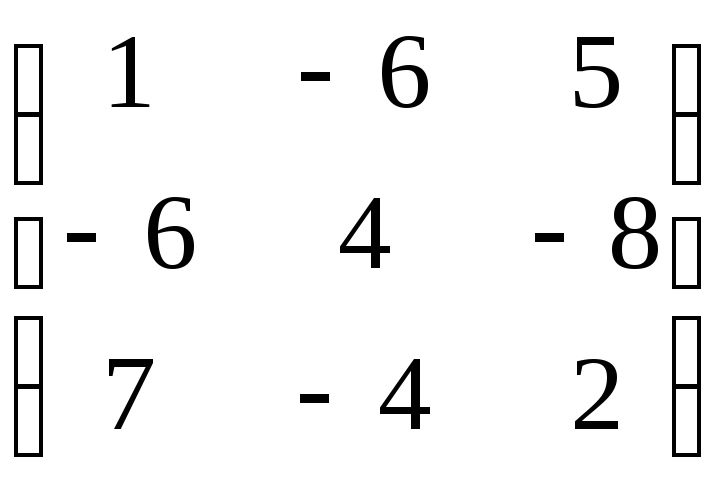 .
.
7.29. 3A + BC, если
A =
![]() ; B =
; B =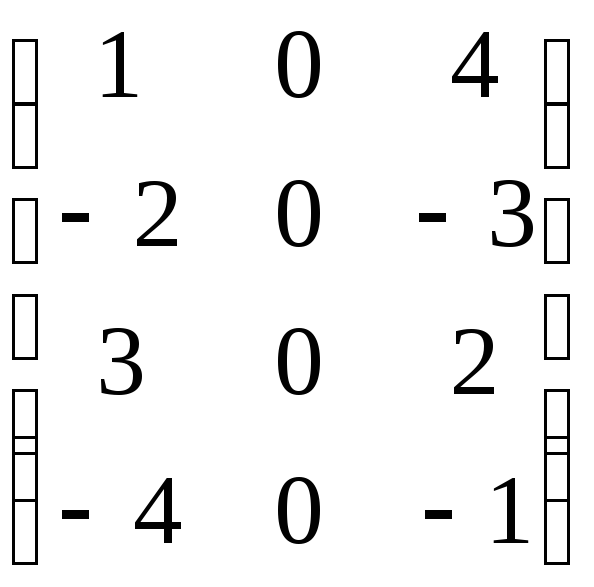 ; С =
; С =
![]() .
.
7.30. 4A – BC, если
A =
![]() ; B =
; B =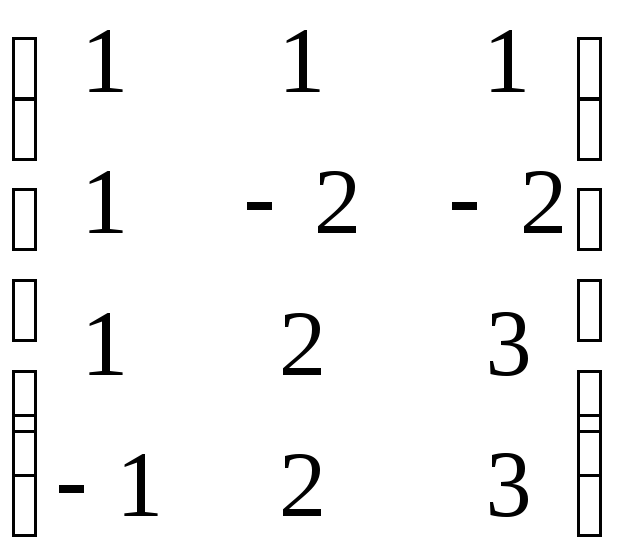 ; С =
; С =
![]() .
.
Задание №8.
Вычислить определитель: 1) разложением по элементам столбца; 4) разложением по элементам строки
8.1.
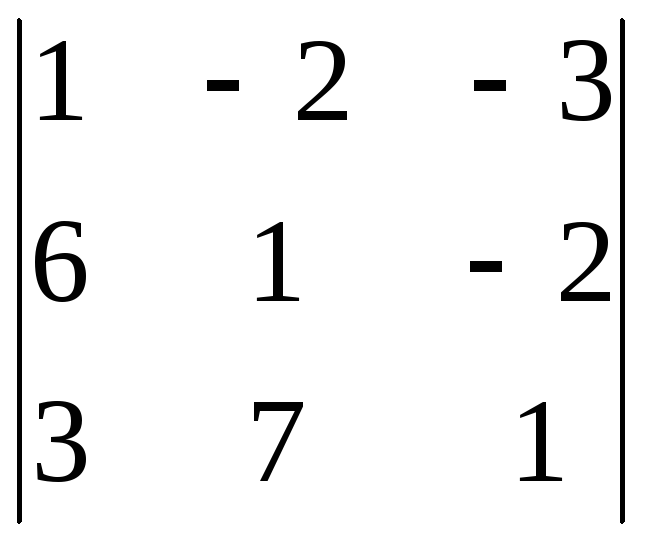 8.2.
8.2. 8.3.
8.3.
8.4.
 8.5.
8.5.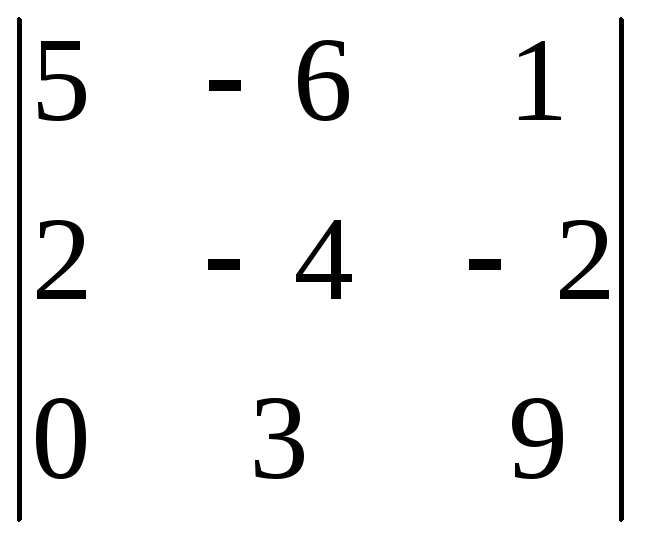 8.6.
8.6.
8.7.
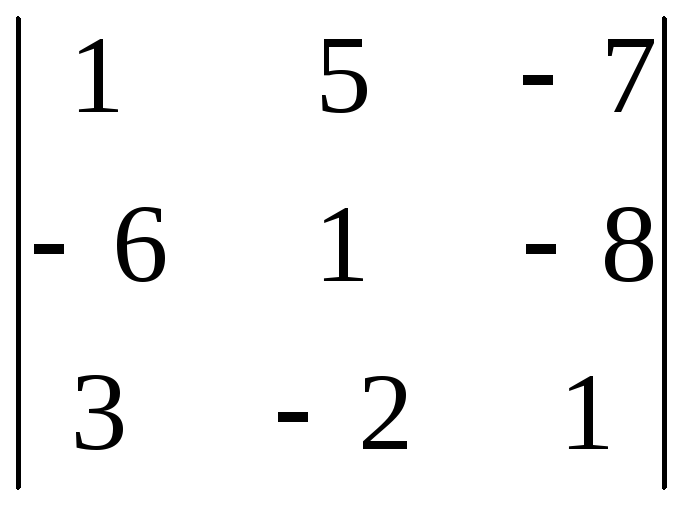 8.8.
8.8. 8.9.
8.9.
8.10.
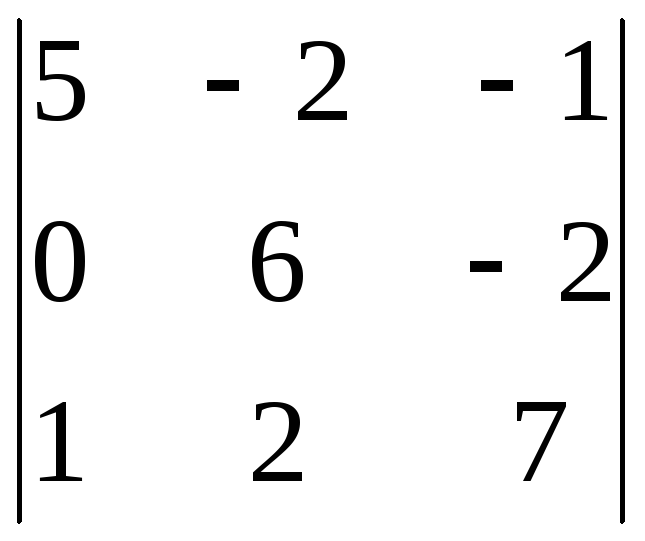 8.11.
8.11.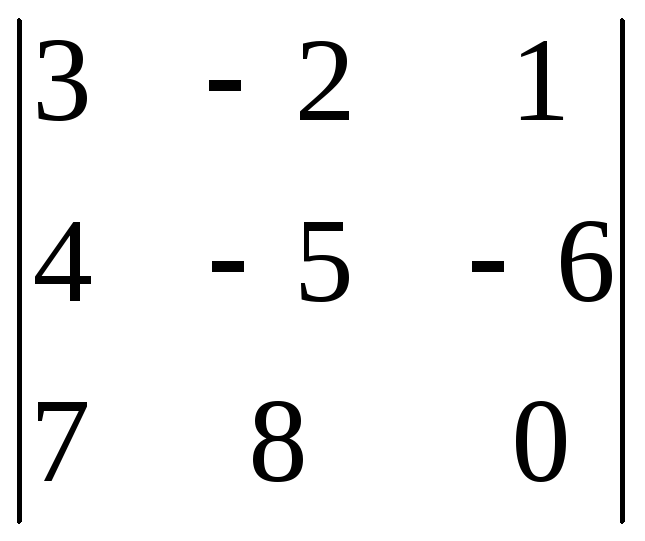 8.12.
8.12.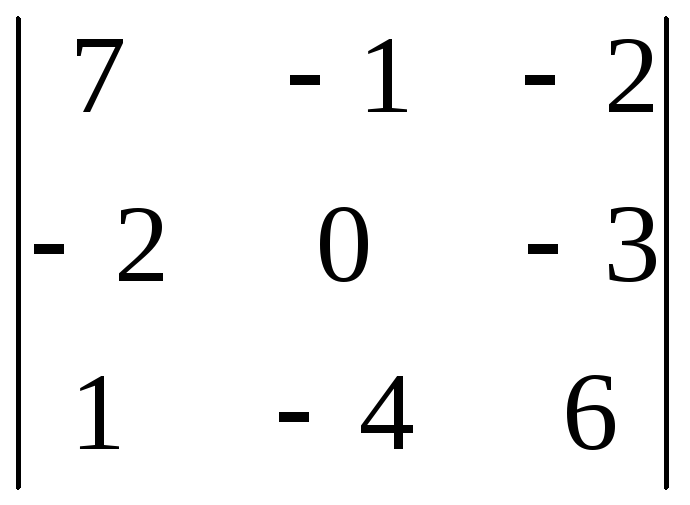
8.13. 8.14.
8.14.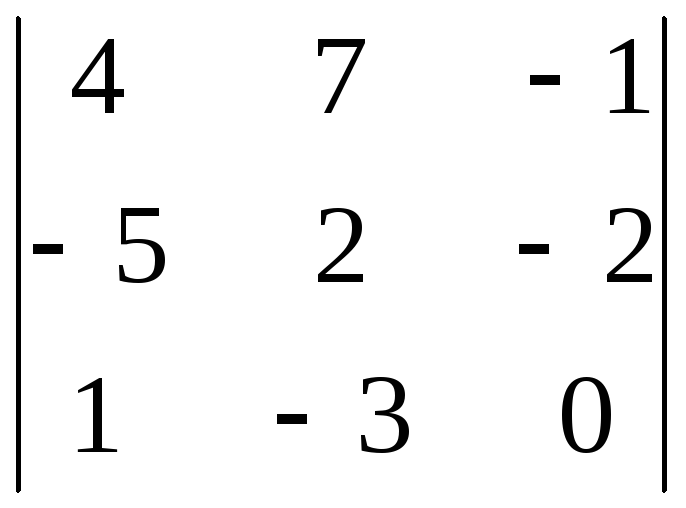 8.15.
8.15.
8.16.
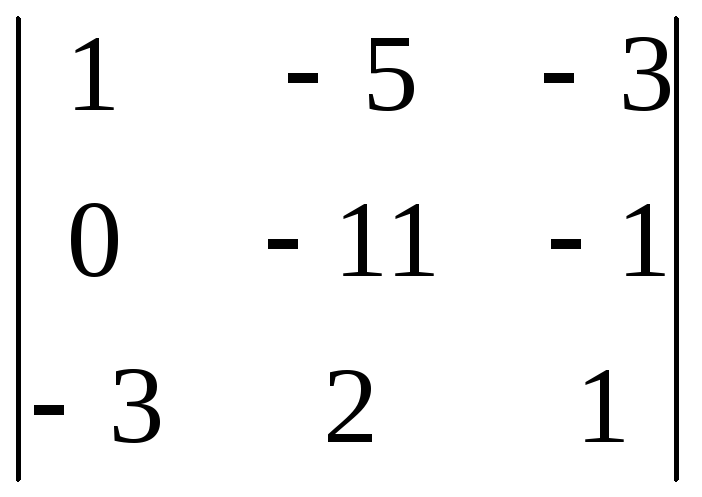 8.17.
8.17.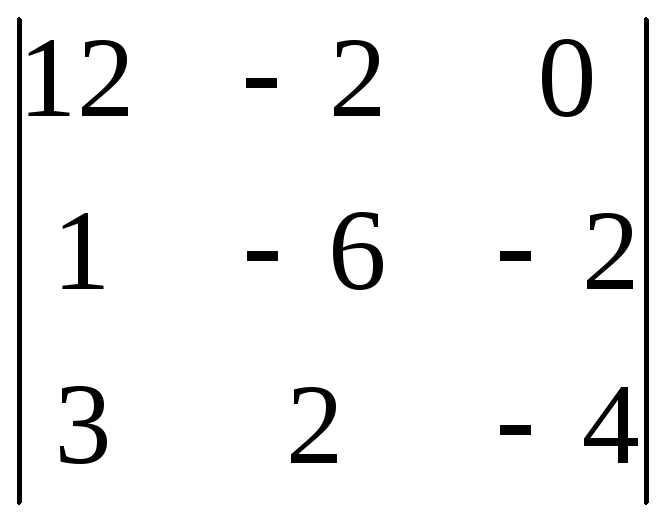 8.18.
8.18.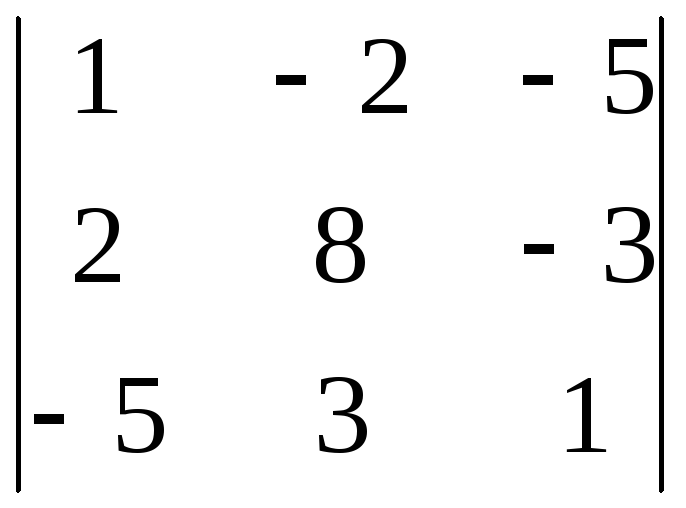
8.19.
 8.20.
8.20. 8.21.
8.21.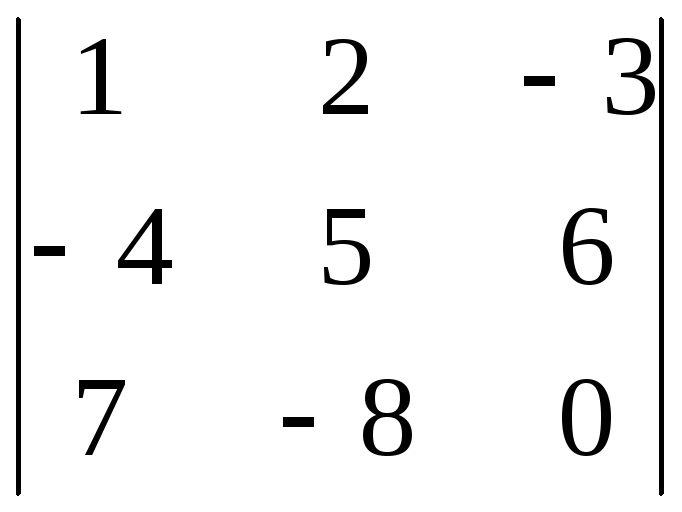
8.22.
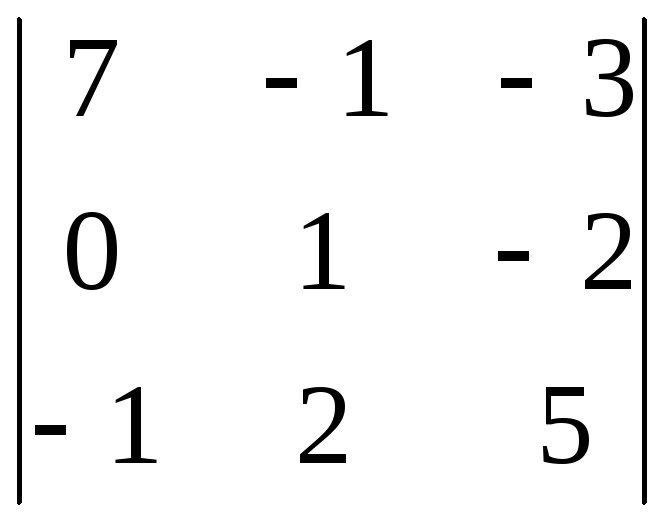 8.23.
8.23. 8.24.
8.24.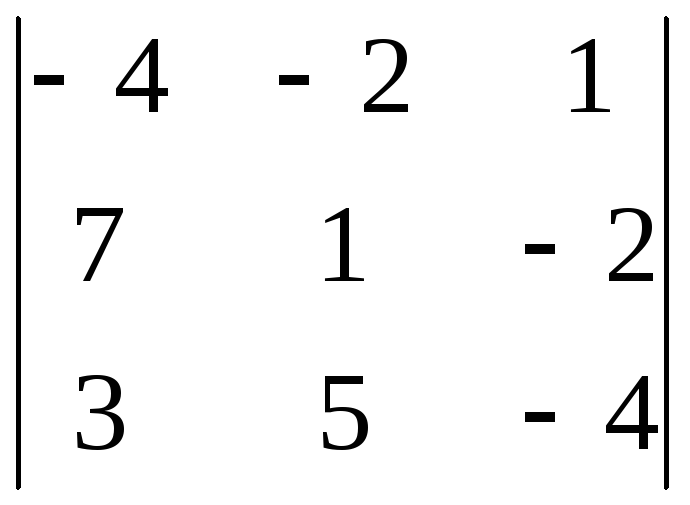
8.25.
 8.26.
8.26. 8.27.
8.27.
8.28.
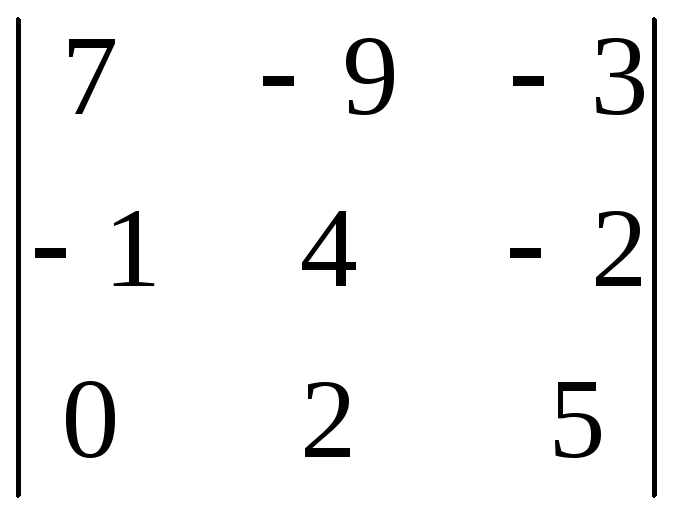 8.29.
8.29.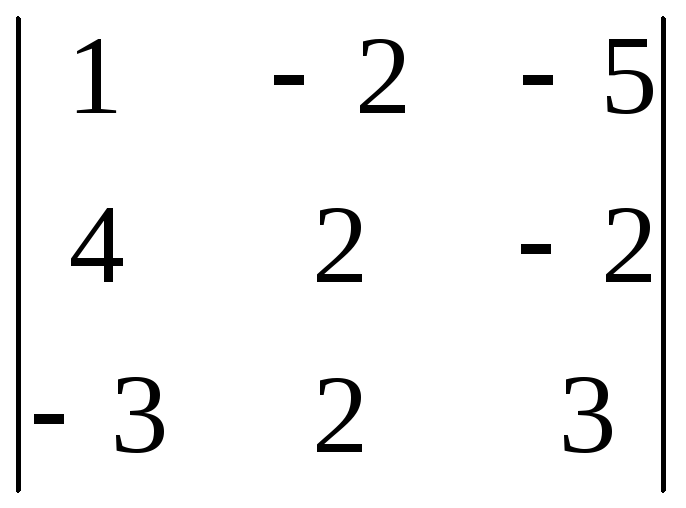 8.30.
8.30.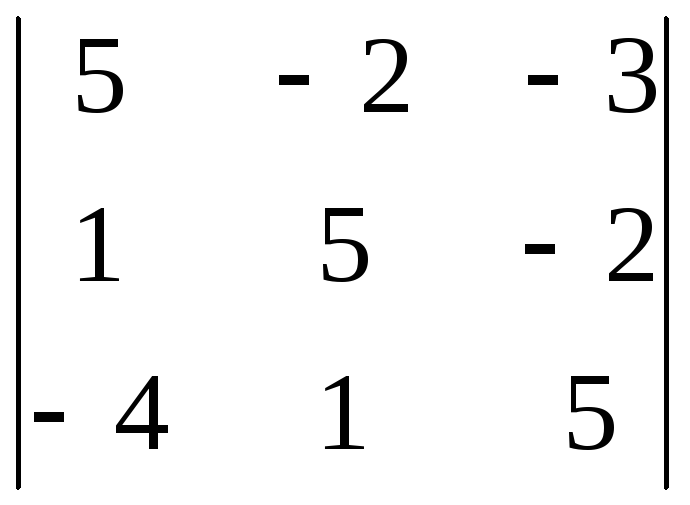
Задание №9.
Вычислить определитель, обнулив элементы (кроме одного) какой-либо строки или столбца исходной матрицы.
9.1.
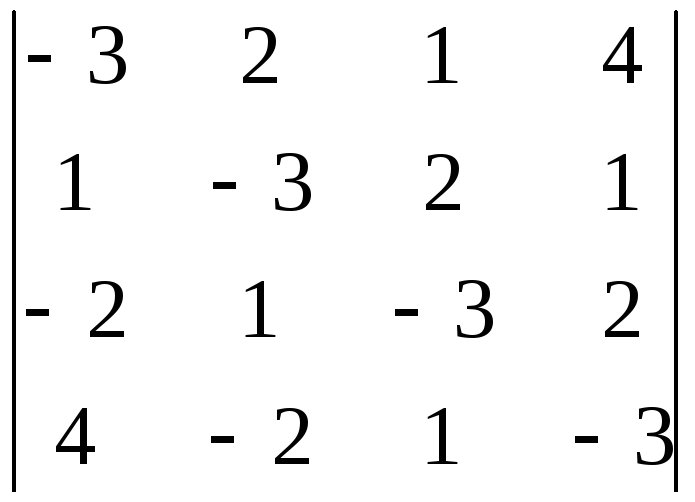 9.2.
9.2. 9.3.
9.3.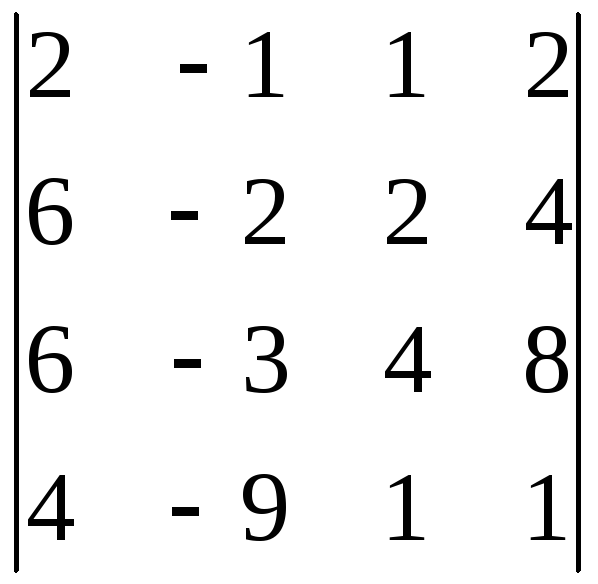
9.4.
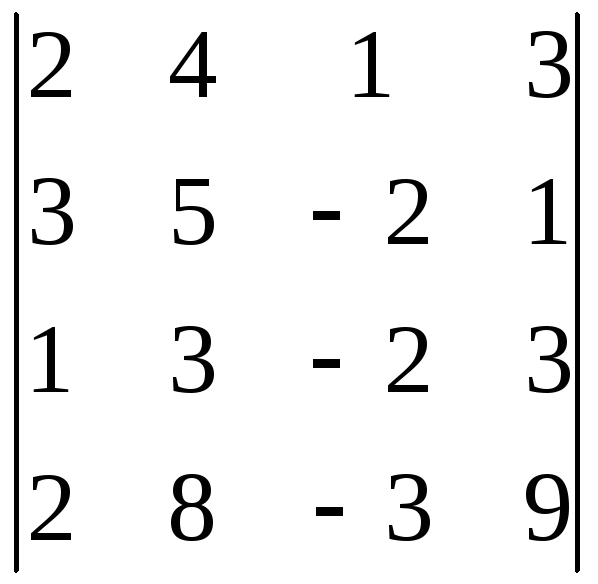 9.5.
9.5.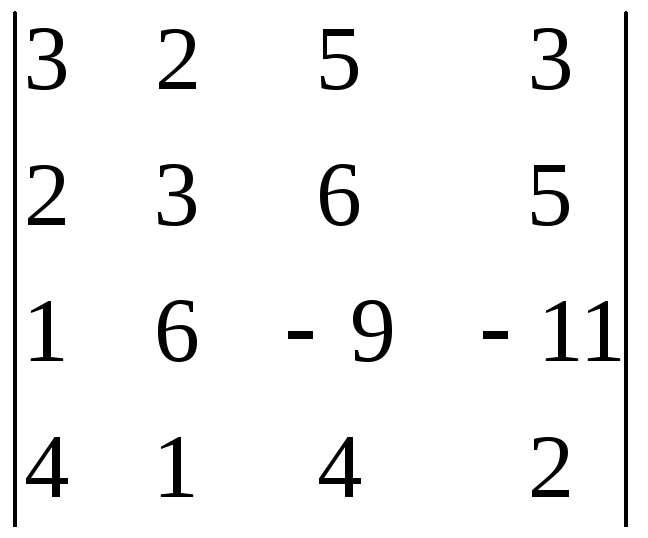 9.6.
9.6.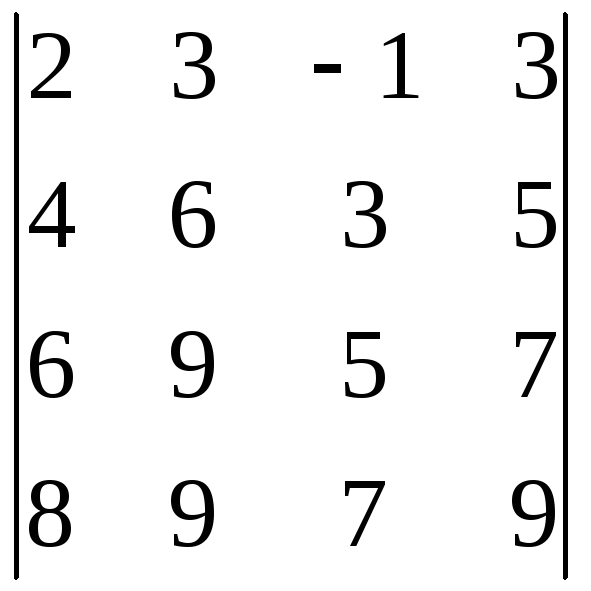
9.7.
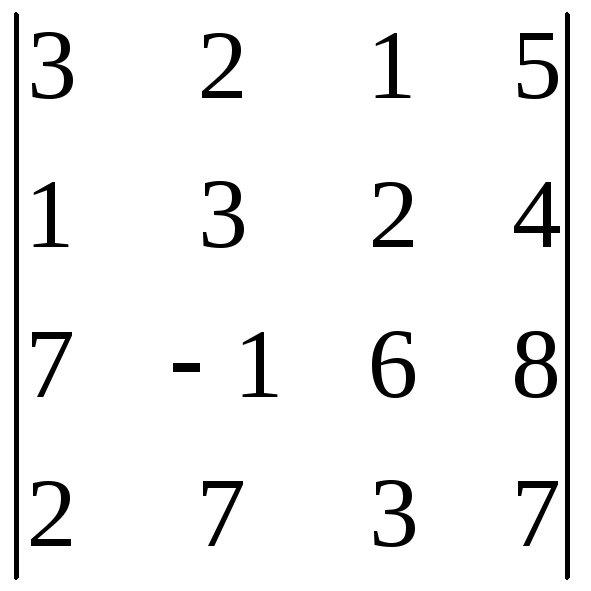 9.8.
9.8. 9.9.
9.9.
9.10.
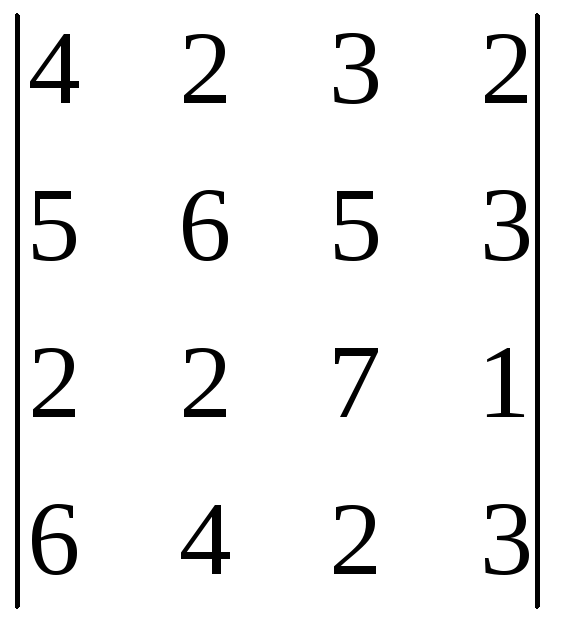 9.11.
9.11.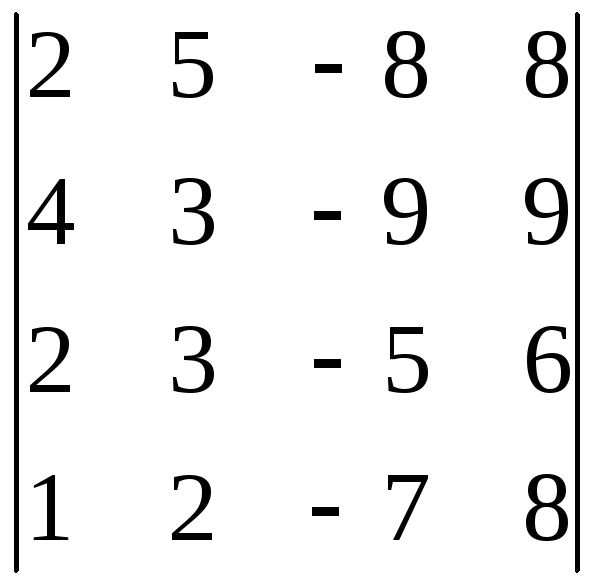 9.12.
9.12.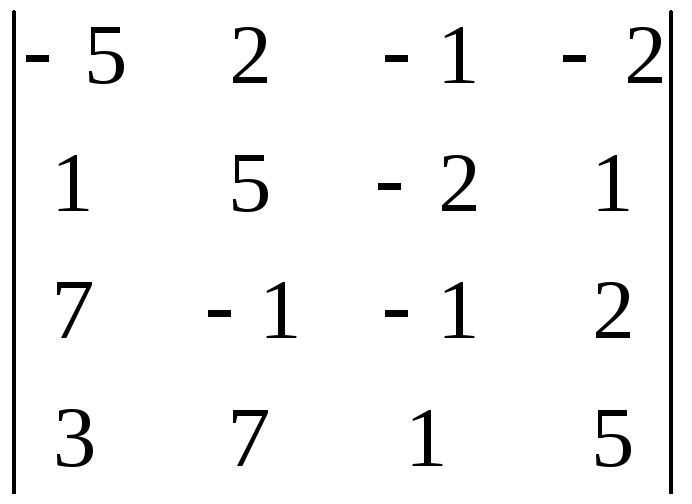
9.13.
 9.14.
9.14. 9.15.
9.15.
9.16.
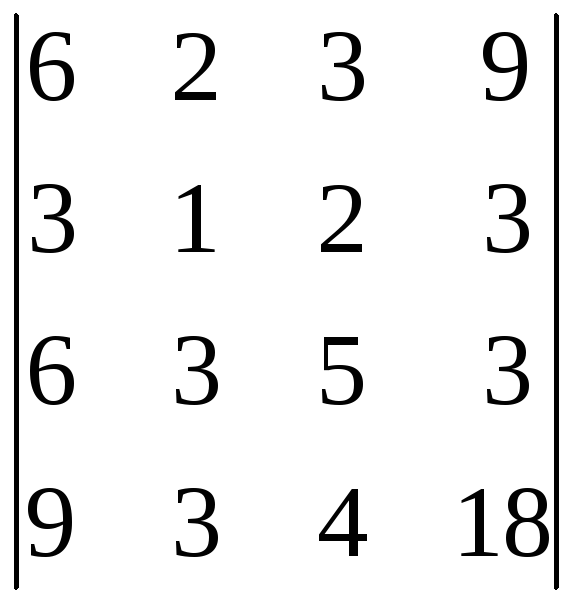 9.17.
9.17. 9.18.
9.18.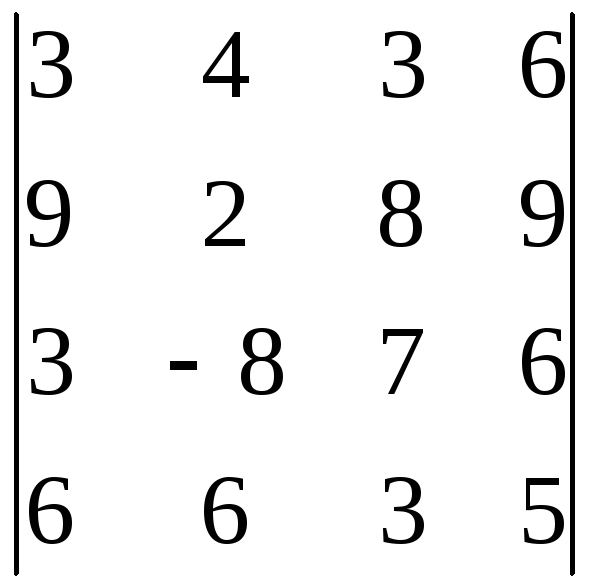
9.19.
 9.20.
9.20. 9.21.
9.21.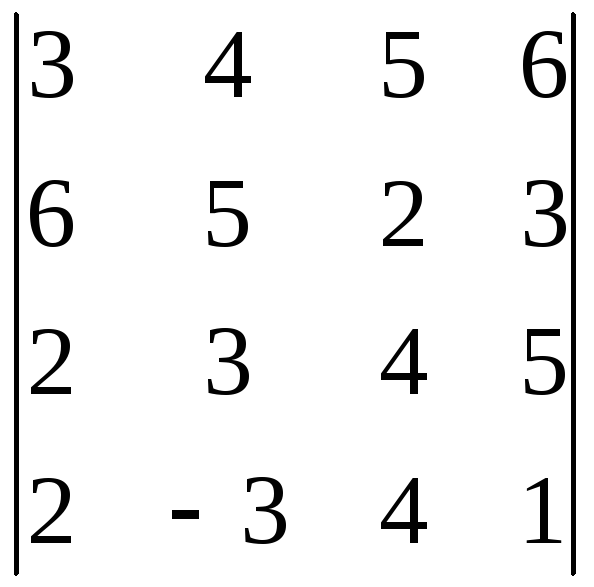
9.22.
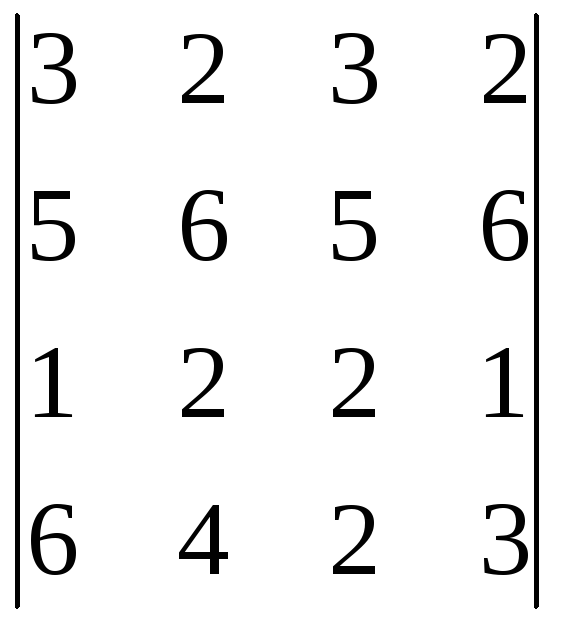 9.23.
9.23. 9.24.
9.24.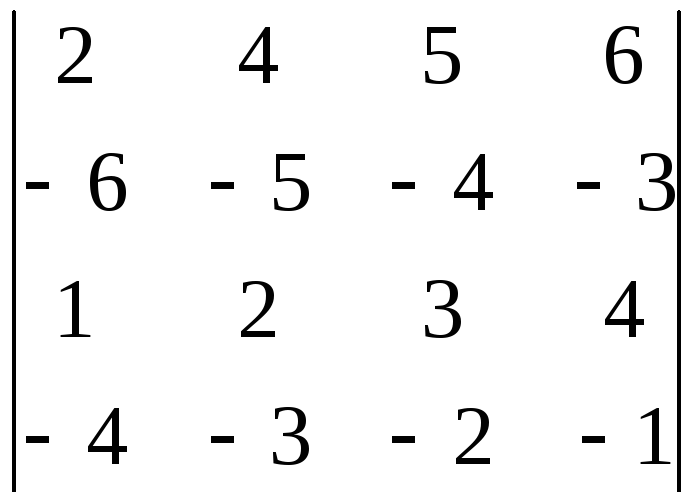
9.25.
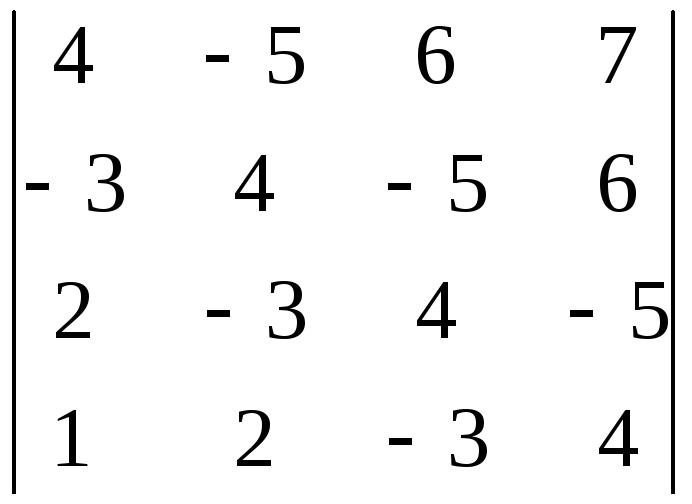 9.26.
9.26. 9.27.
9.27.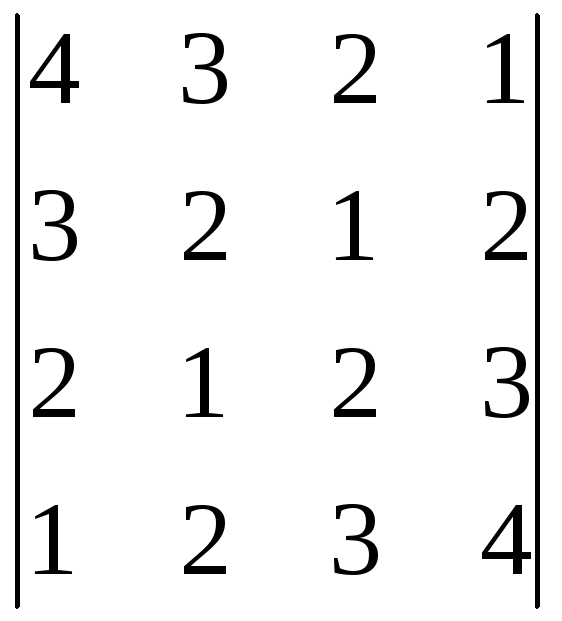
9.28.
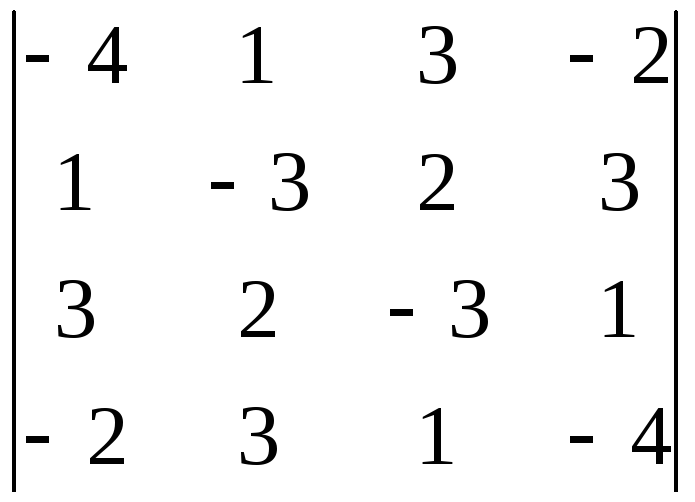 9.29.
9.29. 9.30.
9.30.
Задание №10
Решить систему тремя способами:
а) матричным; б) по формулам Крамера; в) методом Гаусса.
10.1.
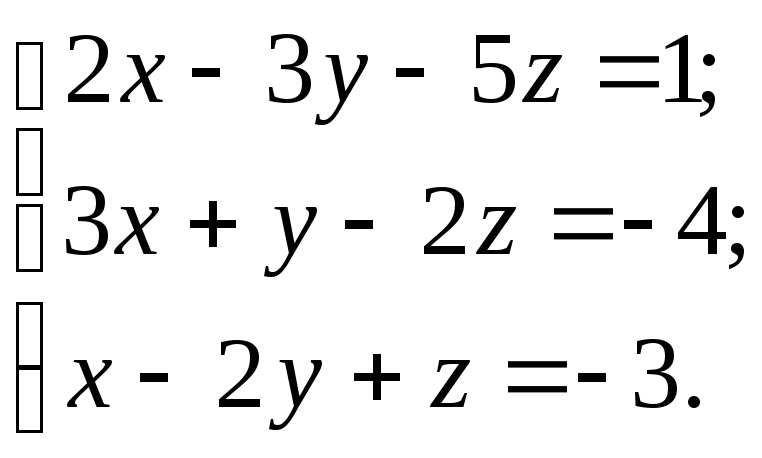 10.2.
10.2.
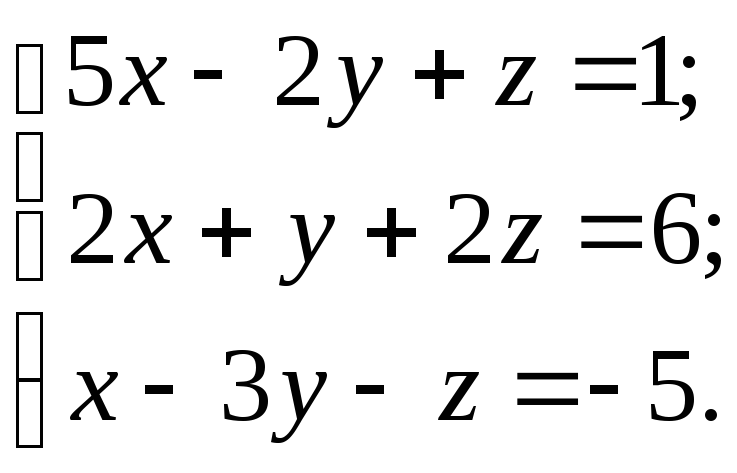 10.3.
10.3.
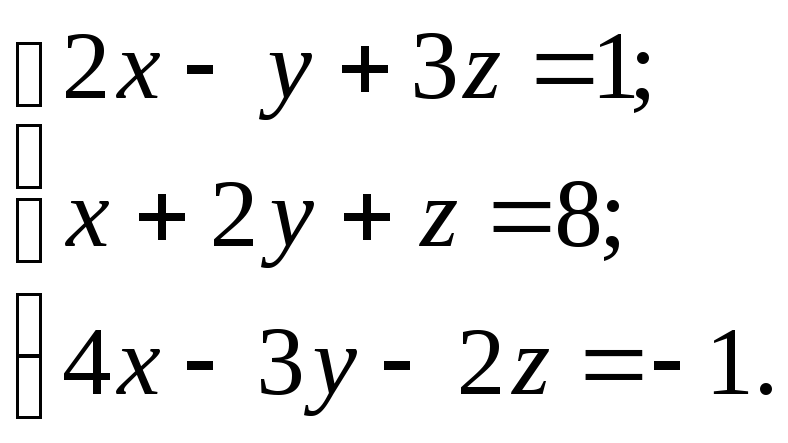
10.4.
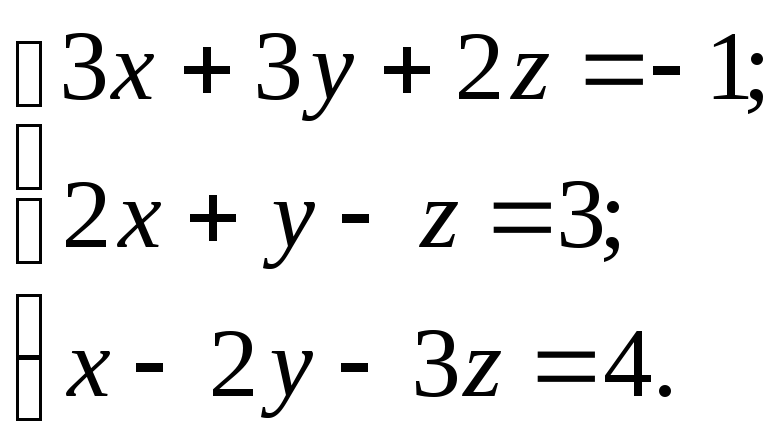 10.5.
10.5.
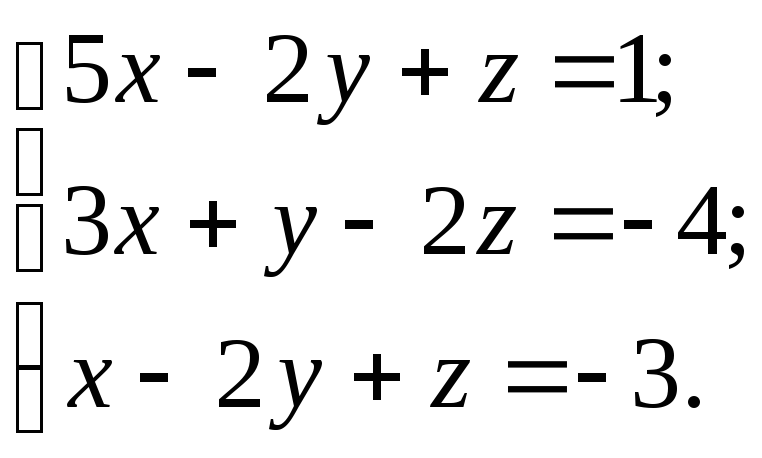 10.6.
10.6.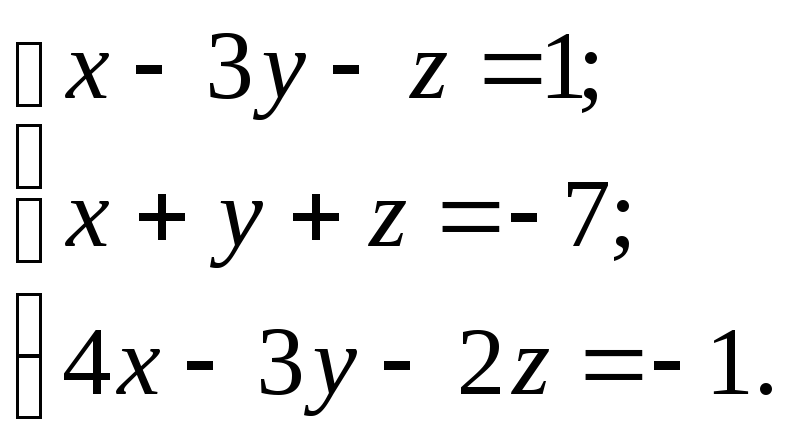
10.7.
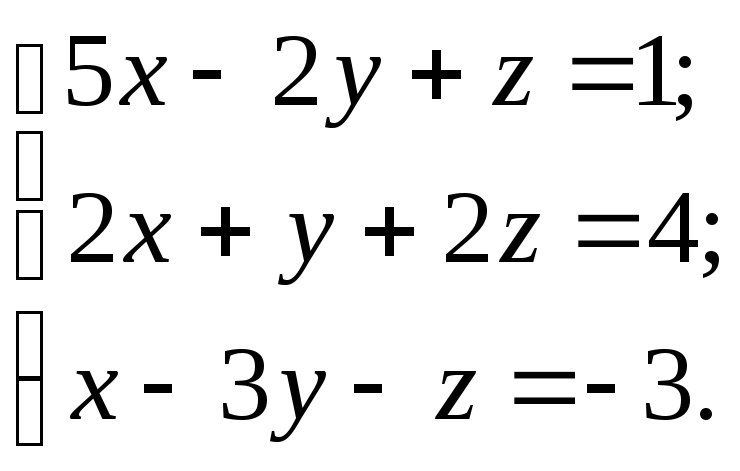 10.8.
10.8.
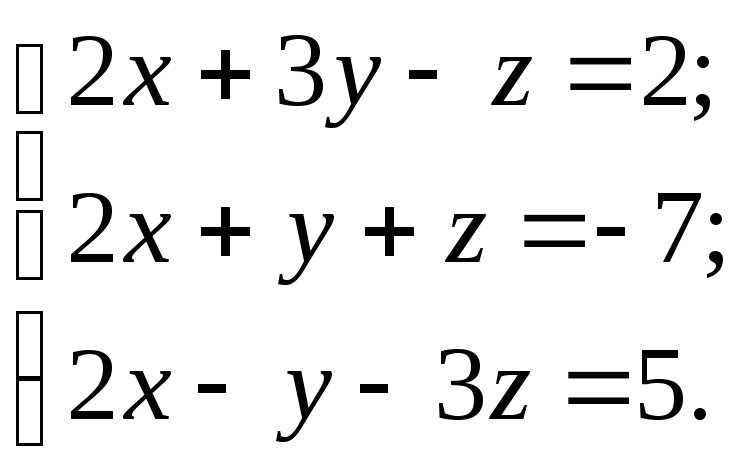 10.9.
10.9.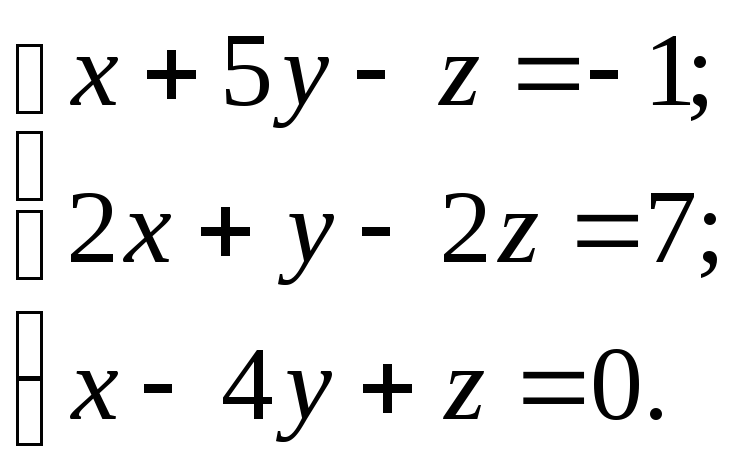
10.10.
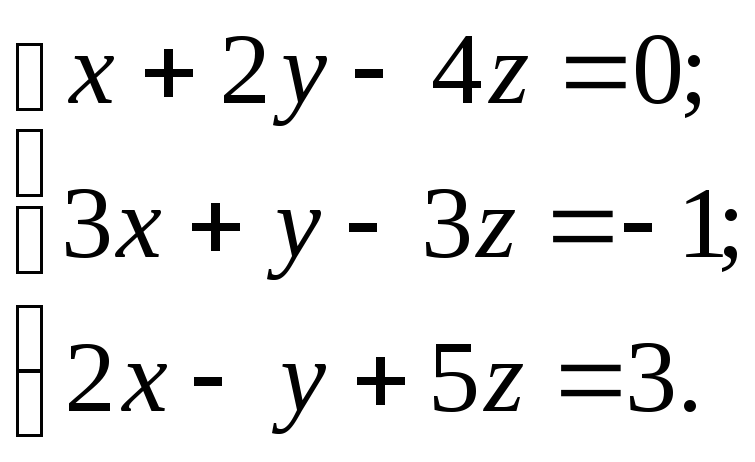 10.11.
10.11.
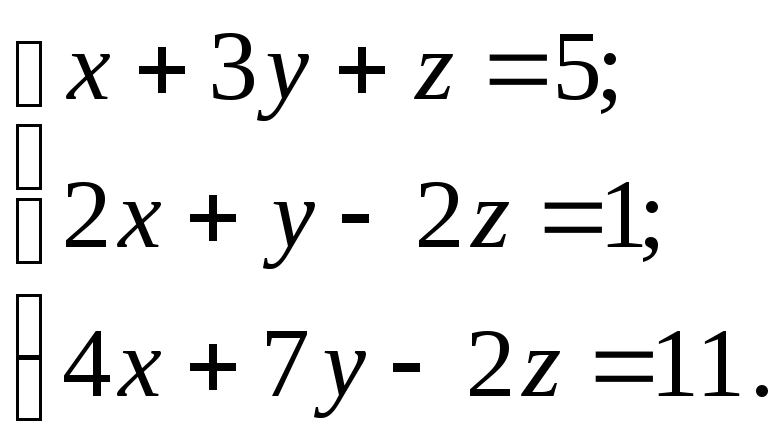 10.12.
10.12.
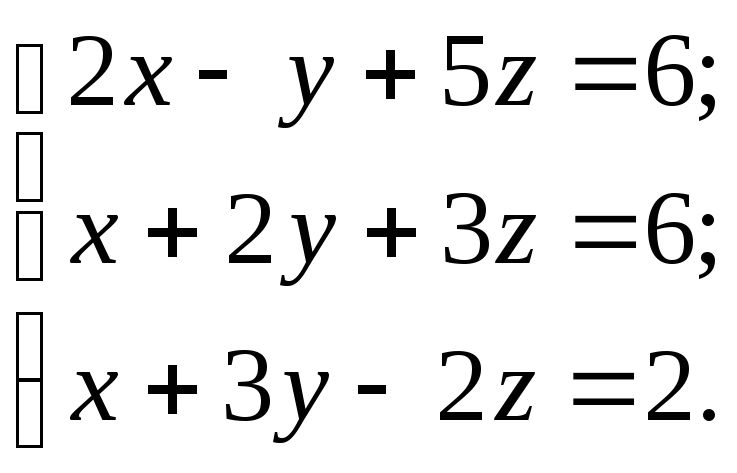
![]()
![]()
![]()
10.13.
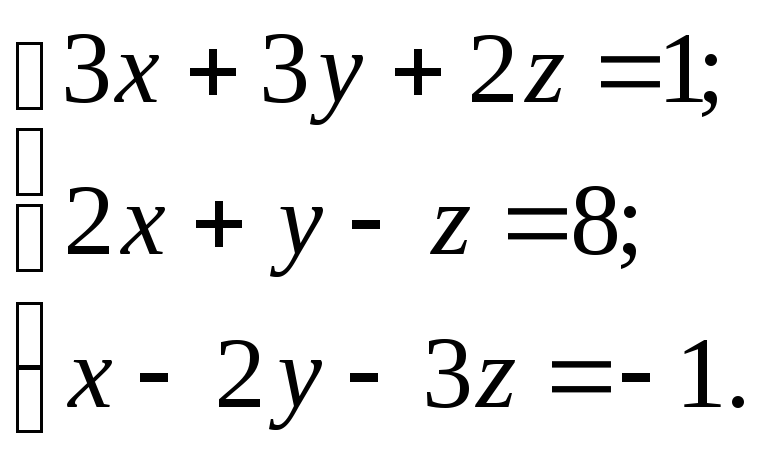
![]() 10.14.
10.14.
 10.15.
10.15.
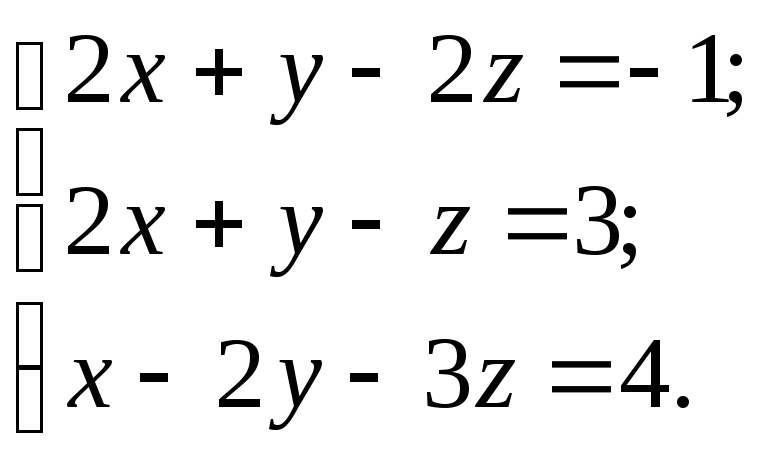
![]()
10.16.
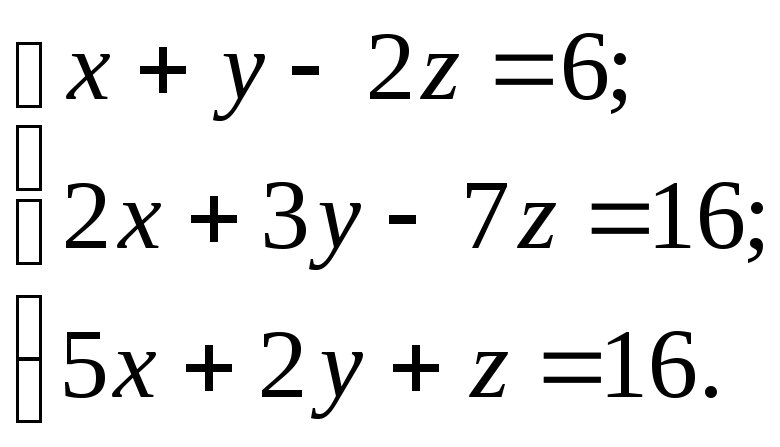 10.17.
10.17.
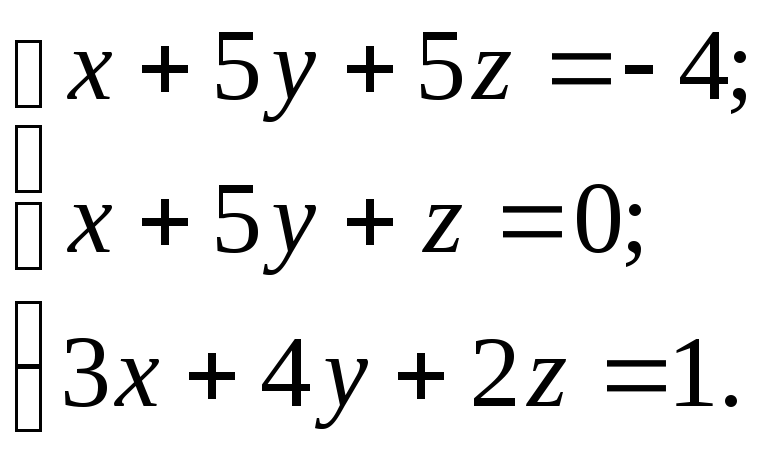 10.18.
10.18.
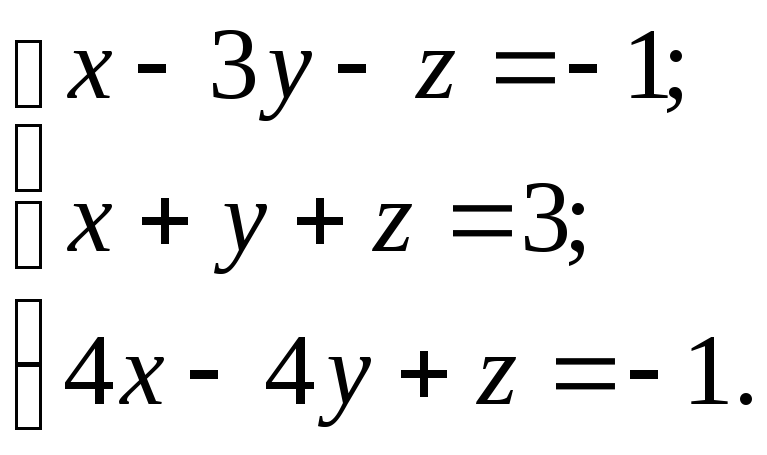
10.19.
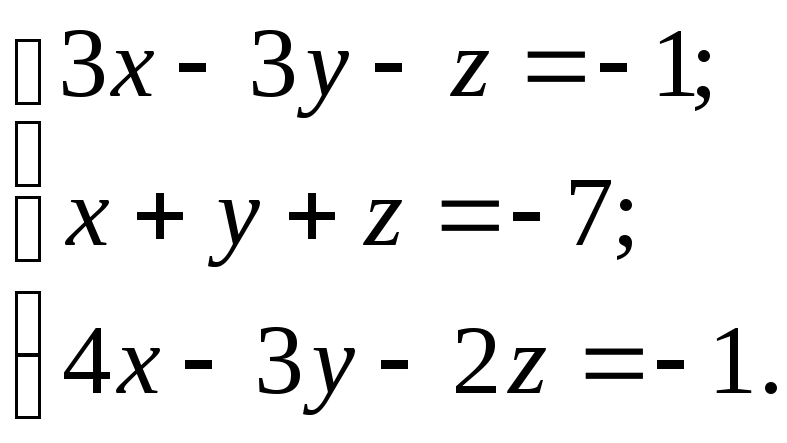 10.20.
10.20.
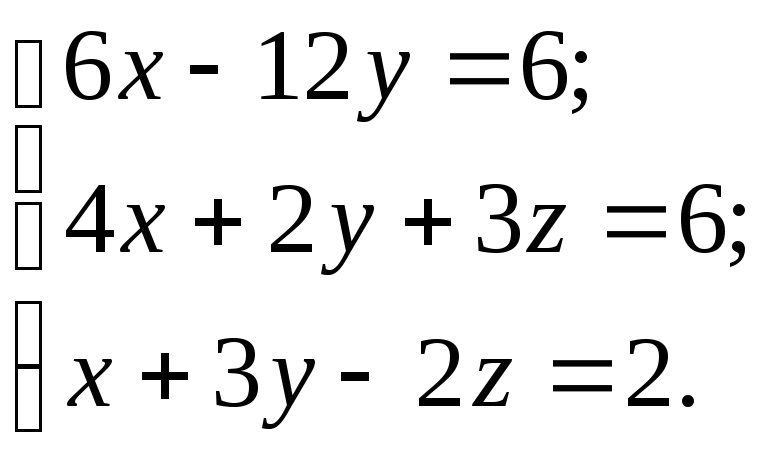 10.21.
10.21.
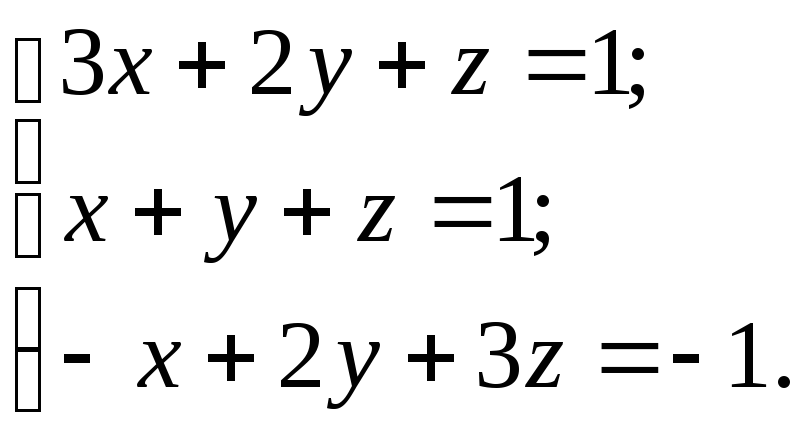
10.22.
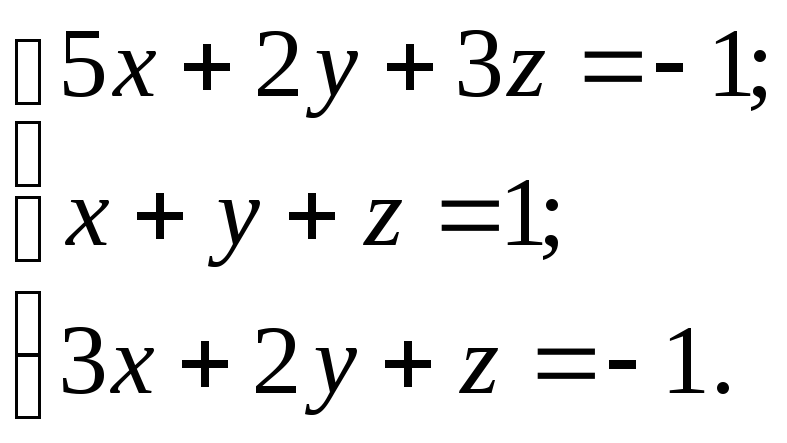 10.23.
10.23.
 10.24.
10.24.
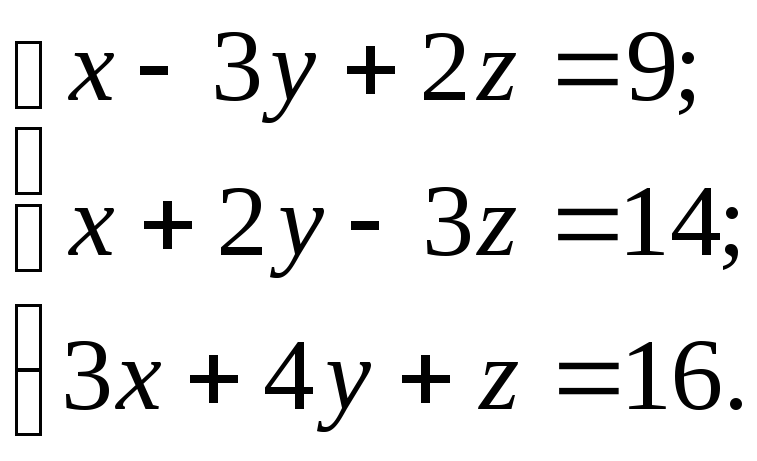
10.25.
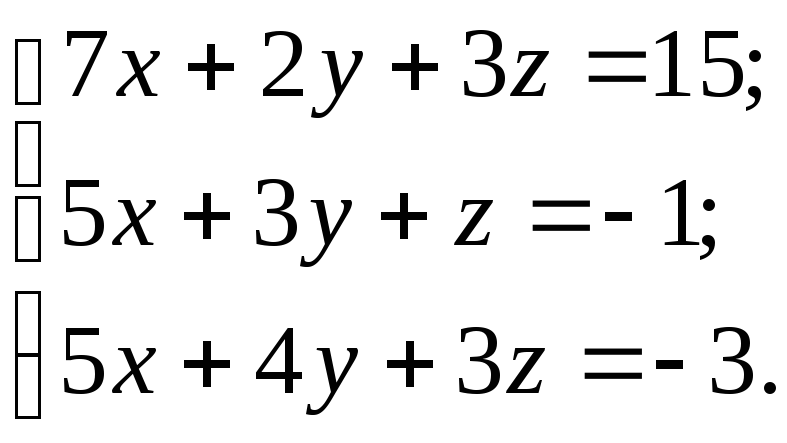 10.26.
10.26.
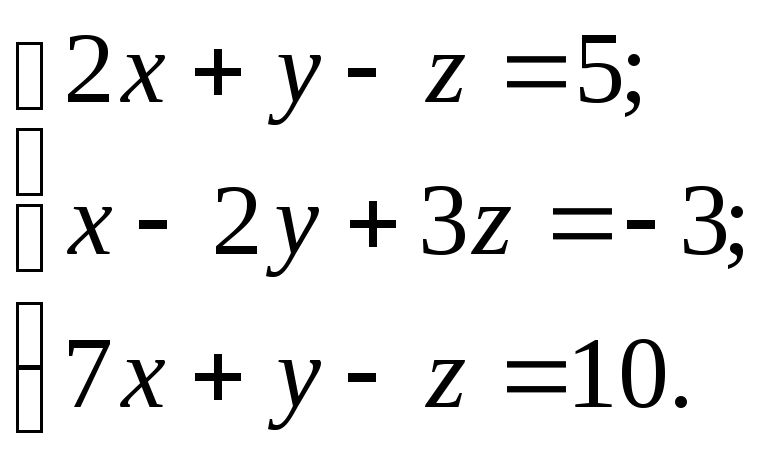 10.27.
10.27.
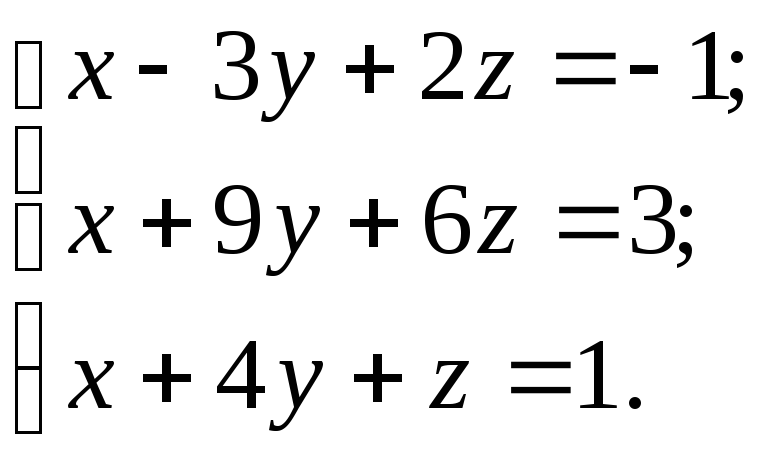
10.28.
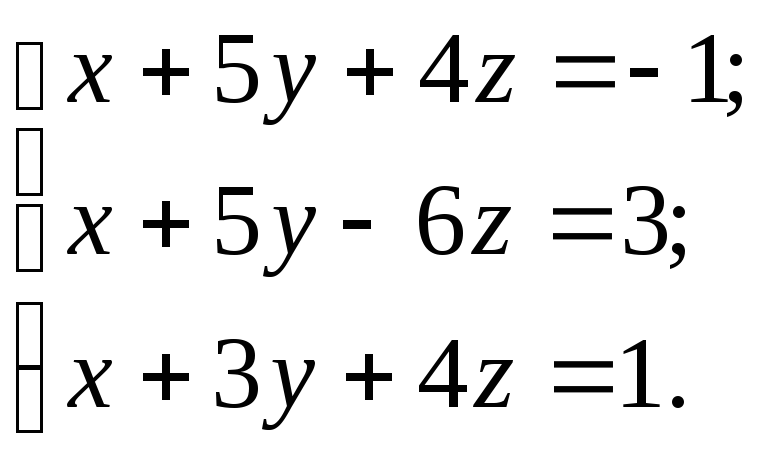 10.29.
10.29.
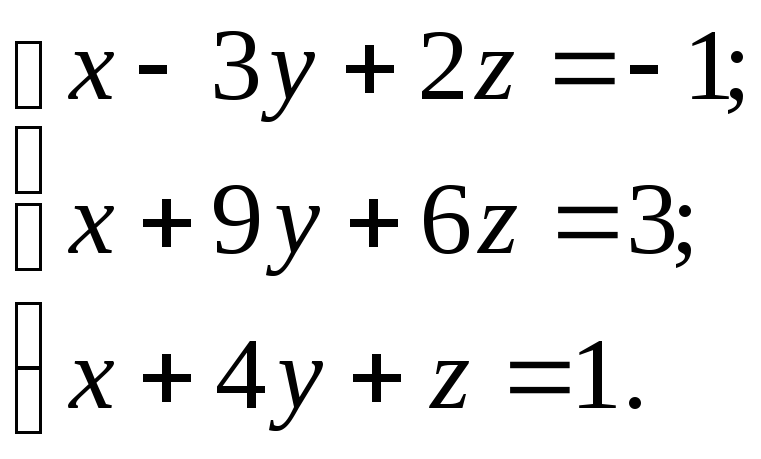 10.30.
10.30.
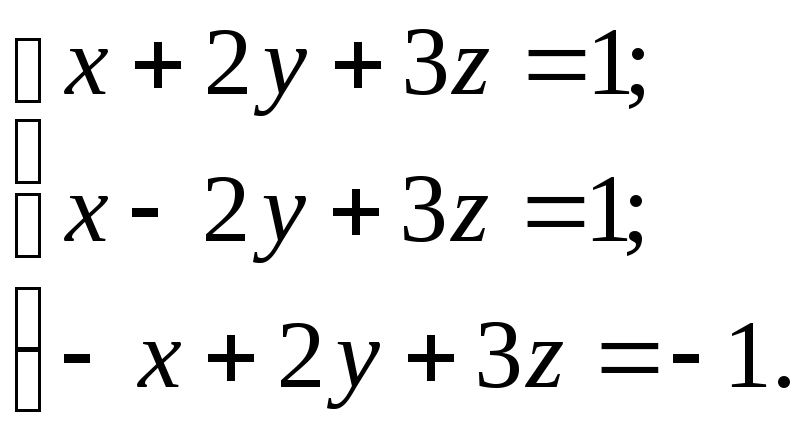
З адание
№11.
адание
№11.
Даны
векторы
![]() и
и
![]() ,
где
,
где
![]() ;
;
![]() ;
;
![]() .
.
Найти:
а)
![]() ;
б)
;
б) ![]() ;
в)
;
в)![]() .
.
11.1.
![]()
11.2.
![]()
11.3.
![]()
11.4.
![]()
11.5.
![]()
11.6.
![]()
11.7.
![]()
11.8.
![]()
11.9.
![]()
11.10.
![]()
11.11.
![]()
11.12.
![]()
11.13.
![]()
11.14.
![]()
11.15.
![]()
11.16.
![]()
11.17.
![]()
11.18.
![]()
11.19.
![]()
11.20.
![]()
11.21.
![]()
11.22.
![]()
11.23.
![]()
11.24.
![]()
11.25.
![]()
11.26.
![]()
11.27.
![]()
11.28.
![]()
11.29.
![]()
11.30.
![]()
Задание №12.
Даны координаты точек M,N,P,Q.
Найти:![]()
косинус угла между ребрами MNиMP; 2) площадь граниMNP;
объем пирамиды MNPQ;
длину высоты пирамиды, опущенной из точки Q.
12.1. M(4,0,0), N(-2,1,2), P(1,3,2), Q(3,2,7).
12.2. M(-2,1,2), N(4,0,0), P(3,2,7), Q(1,3,2).
12.3. M(1,3,2), N(3,2,7), P(4,0,0), Q(-2,1,2).
12.4. M(3,2,7), N(1,3,2), P(-2,1,2), Q(4,0,0).
12.5. M(3,1,-2), N(1,-2,1), P(-2,1,0), Q(2,2,5).
12.6. M(1,-2,1), N(3,1,-2), P(2,2,5), Q(-2,1,0).
1.7. M(-2,1,0), N(2,2,5), P(3,1,2), Q(1,-2,1).
12.8. M(2,2,5), N(-2,1,0), P(1,-2,1), Q(3,1,2).
12.9. M(1,-1,6), N(4,5,-2), P(-1,3,0), Q(6,1,5).
12.10. M(6,1,5), N(-1,3,0), P(4,5,-2), Q(1,-1,6).
12.11. M(-5,-1,8), N(2,3,1), P(4,1,-2), Q(6,3,7).
12.12. M(5,1,-4), N(1,2,-1), P(3,3,-4), Q(2,2,2).
12.13. M(1,1,1), N(2,3,4), P(4,3,2), Q(3,2,4).
12.14. M(1,1,2), N(2,3,-1), P(2,-2,4), Q(-1,1,3).
12.15. M(2,-3,5), N(0,2,1), P(-2,-2,3), Q(3,2,4).
12.16. M(1,-3,-4), N(-1,0,2), P(2,-4,-6), Q(1,1,1).
12.17. M(2,1,-2), N(3,3,3), P(1,1,2), Q(-1,-2,-3).
12.18. M(1,1,1), N(2,0,2), P(2,2,2), Q(3,4,-3).
12.19. M(0,0,0), N(1,1,0), P(2,1,0), Q(0,0,6).
12.20. M(0,0,0), N(4,1,1), P(1,1,0), Q(0,0,8).
12.21. M(1,2,-1), N(0,1,5), P(-1,2,1), Q(2,5,3).
12.22. M(1,-1,2), N(5,-6,2), P(1,3,-1), Q(2,3,1).
12.23. M(2,-1,1), N(5,5,4), P(3,2,-1), Q(4,1,3).
12.24. M(2,3,1), N(4,1,-2), P(6,3,7), Q(-5,-4,8).
12.25. M(2,1,-1), N(3,0,1), P(2,-1,3), Q(0,8,0).
12.26. M(2,-3,1), N(B,1,-1), P(4,8,-9), Q(2,-1,2).
12.27. M(5,-1,-4), N(9,3,-6), P(7,10,-14), Q(5,1,-3).
12.28. M(1,-4,0), N(5,0,-2), P(3,7,-10), Q(1,-2,1).
12.29. M(-3,-6,2), N(1,-2,0), P(-1,5,-8), Q(-3,-4,3).
12.30. M(-1,1,-5), N(3,5,-7), P(-1,3,-4).
Задание № 13.
Доказать, что векторы
![]() образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора
![]() в этом базисе.
в этом базисе.
13.1.
![]()
13.2.
![]()
13.3.
![]()
13.4.
![]()
13.5.
![]()
13.6.
![]()
13.7.
![]()
13.8.
![]()
13.9.
![]()
13.10.
![]()
13.11.
![]()
13.12.
![]()
13.13.
![]()
13.14.
![]()
13.15.
![]()
13.16.
![]()
13.17.
![]()
13.18.
![]()
13.19.
![]()
13.20.
![]()
13.21.
![]()
13.22.
![]()
13.23.
![]()
13.24.
![]()
13.25.
![]()
13.26.
![]()
13.27.
![]()
13.28.
![]()
13.29.
![]()
13.30.
![]()
