METHOD / МКП / Lab_MathCAD / Лаб_раб_MathCAD

Министерство образования и науки Украины

Приазовский государственный технический университет

Кафедра технологии машиностроения

Лещенко А.И.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторной работы

«Система обработки информации»

по курсу: «МИКРОПРОЦЕССОРНОЕ УПРАВЛЕНИЕ ТЕХНОЛОГИЧЕСКИМИ СИСТЕМАМИ»

(для студентов специальности 7.090202 «Технология машиностроения»

дневной и заочной форм обучения)

УТВЕРЖДЕНО

На заседании кафедры

технологии машиностроения

Протокол № 10 от 4.10.06

Мариуполь 2006 г.

УДК 621. (077)

Методические указания к выполнению лабораторной работы «Система обработки информации» по курсу: «Микропроцессорное управление технологическими системами»./ Состав. : Лещенко А. И – Мариуполь, ПГТУ, 2006 г. – 9 с.

Предназначены для студентов дневной и заочной форм обучения специальности 7.09.02.02. «Технология машиностроения». Содержат указания по выполнению лабораторной работы.

Составители: А.И. Лещенко ст. преподаватель

Отв. за выпуск А. А. Андилахай, доц.

1.Система обработки информации.

Под информацией в широком смысле принято понимать различные сведения о событиях в общественной жизни, явлениях природы, о процессах в в технических устройствах. Она содержится в нашей речи, в текстах книг и газет, в показаниях, измерительных приборов и отображает разнообразие, присущее объектам и явлениям реального мира. Информацию, воплощенную и зафиксированную в некоторой материальной форме, называют сообщением и передают с помощью сигналов.

На вход системы сигналы от источников информации могут поступать на носителях любой физической природ (сигналы датчиков, магнитные ленты, перфокарты, перфолеты, цифры, буквы и т. д.). Ввод исходных данных в основное устройство обработку (процессор) осуществляется преимущественно в двух формах:

- в режиме непосредственной связи с исследуемы объектом (прямой ввод), когда ввод сигналов в процессор осуществляется в реальном времени (информа-ция о состоянии поведении объекта поступает с датчиков, воспринимающим сигналы о состоянии процессов);

- в режиме предварительного преобразования информации (перегруппировка, кодирования преобразования аналого-цифровые и т. д.) к виду, удобном для последующей автоматической обработки в процессоре. Второй режим важен для исследовательской практики, та как он позволяет вести оперативную обработку результатов получаемых при многократных экспериментах.

В качестве основного устройства обработки могут использоваться универсаль-ные или специализированные вычислительные машины.

Выдача результатов обработки может осуществляться так же в двух формах:

1) в режиме прямой связи с потребителями информации (прямой вывод), когда преобразованная информация, минуя буферное накопление, сортировку и устройств; представления результатов, непосредственно выводится на исполнительное устройство в виде сигналов;

2) в режиме буферного накопления с использованием устройств представле-ние результатов обработки потребителю.

Управление всей работой системы осуществляется с помощью центрального процессора или микропроцессора, где выполняются арифметические и логические операции.

Передача информации предполагает наличие, как минимум двух объектов - источника информации и приемника информации. Для передачи информации применяются сигналы,

Сигналом называется физический процесс (например, определенная последовательность электрических импульсов), однозначно соответствующий данному сообщению.

Отображение множества состояний источника информации во множество состояний сигнала (носителя) называют кодированием, а отображение множества состояний сигнала во множество состояний приемника - декодированием.

Источники информации и создаваемые ими сообщения разделяют на непрерывные и дискретные. Непрерывные сообщения отображаются сигналами, представляющими собой какие-либо физические величины, изменяющиеся непрерывно и принимающие бесконечное число значений в некотором диапазоне. К ним относятся изменение тока, мощности, расход жидкости, топлива и др. Такая форма представления информации используется в аналоговых, моделирующих и вычислительных устройствах. Дискретные сообщения состоят из конечного множества элементов, формируемых источником информации. К дискретным сообщениям относятся позиционные или предельные извещения. Например, <включено выключено>, <открыто-закрыто> и т.д.

Дискретные сообщения отображаются сигналами, принимающими конечное число значений.

Единицами количества информации в цифровых системах являются:

бит - это такое количество информации, которое характеризует источник с двумя равновероятными состояниями;

байт - это количество информации, состоящее из 8 бит; слово длиной в один байт позволяет закодировать 2⁸ = 256 различных символов, что. практически достаточно для обработки символьной информации (см. ASCII коды);

килобайт -1024=10¹⁰ бит единица двоичной информации, соответствующая 128 байтам, следовательно один килобайт может содержать 128 символов ASCII таблицы;

мегабайт – 1048576=10²⁰ байт

Кроме перечисленных единиц информации используют такие понятия: поле - это группа бит, имеющих определенное назначение; массив - совокупность полей, байтов или слов, объединенных общим признаком (например, исходные данные);

массивов, сгруппированных с целью наименования.

Для характеристики скорости передачи информации используют единицу бод - это 1 бит/с.

Рис. 1 Аналоговое задающее устройство

Непрерывный сигнал, возникающий на выходе какого-либо устройства или датчика (температуры, давления, скорости), называется аналоговым. Рассмотрим схему задающего устройства (рис. 1). Кулачек 1 вращается с угловой скоростью w. Ролик штока 2 поджимается к профилю кулачка R=f(A) пружиной, при этом сам шток при повороте кулачка на угол А движется поступательно. Жестко связанный со штоком ползун 3 снимает напряжение с реостата R, изменение которого можно наблюдать по шкале вольтметра V или на экране осциллографе ТС.

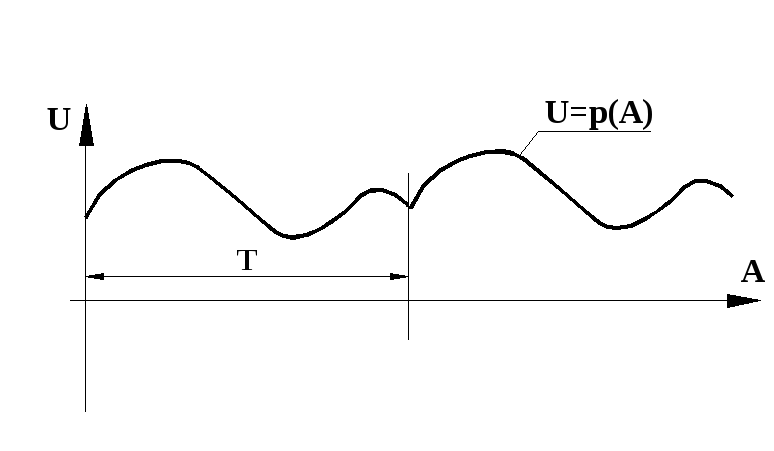
Рис. 2 График изменения выходного сигнала аналогового устройства

На рис. 2 показан график изменения выходного сигнала U=p(A) с периодом T=k(w).

В системах с высокой надежностью и сравнительно простым алгоритмом вычислений применяют АВМ – аналоговые вычислительные машины. Простей-шая «АВМ» - вольтметр, принцип действия которого основан на законе Ома – , т.е. при изменении сомножителей сила тока I и сопротивление R можно получить произведение – напряжение U.

Главный недостаток АВМ – низкая гибкость, т.е. изменения алгоритма ее работы. Поэтому в настоящее время АВМ все в большей степени заменяются на ЦВМ – цифровые вычислительные машины, основой которых являются микропроцессоры.

Замена аналогового сигнала на цифровой называется оцифровкой, а блоки выполняющие это АЦП – аналогово цифровые преобразователи.

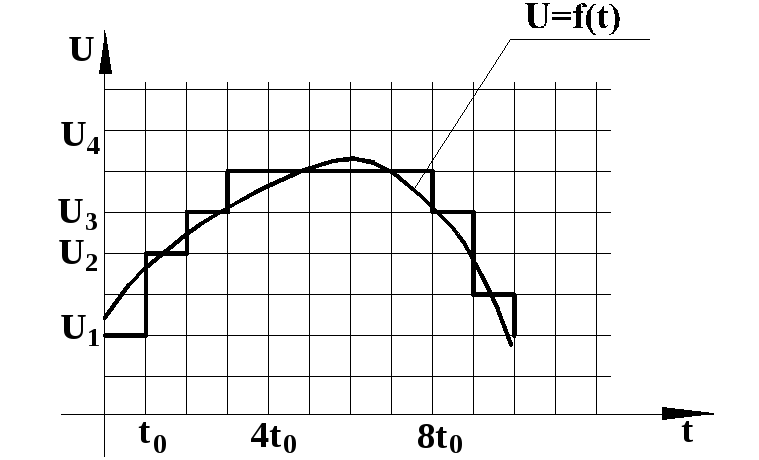
Рис. 3 Схема оцифровки сигнала U=f(t)

Процесс аналогоцифрового преобразования состоит из дискретизации, т.е. замену значений непрерывного сигнала U=f(t) рядом значений U₁, U₂, U₃ .... (рис. 3) измеренных в дискретные моменты времени t₀, 2t₀, 3t₀ . . . , где t₀ – период дискретизации. Этот процесс можно иллюстрировать следующим примером. Один абонент хочет передать другому по телефону график изменения, какого либо процесса. Он говорит: «Возьми лист бумаги и нарисуй на ней сетку с таким интервалом. Я буду диктовать тебе координаты точек». После этого абонент «приемник» соединит точки плавной кривой и примерно получит график.

Таким образом, непрерывный (аналоговый) сигнал, ряд числовых значений заменяет ступенчатый сигнал. Такой процесс преобразования из-за слишком большого t₀ может привести к значительной погрешности. Однако при слишком малой величине t₀ возникают проблемы с быстродействием системы преобразо-вания, ее сложностью и высокой стоимостью.

Поле оцифровки числовые значения сигнала могут быть представлены двоичным кодом (0, 1) и переданы или записаны на диск сигналами одинаковой амплитуды но разного знака (рис. 4).

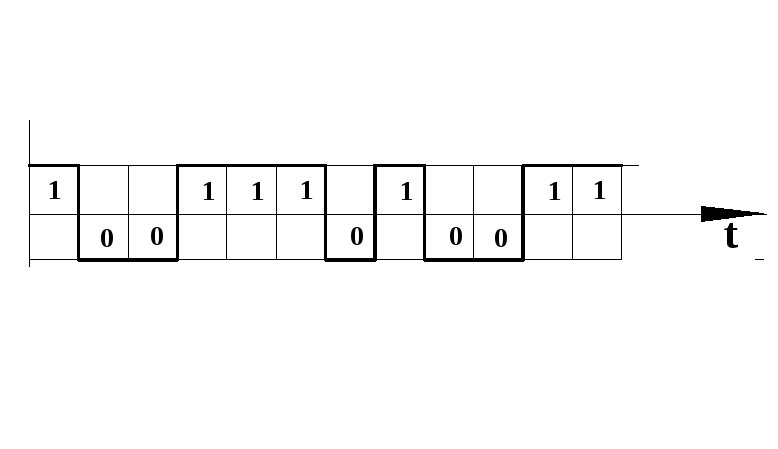
Рис. 4 Кодирование информации двоичным сигналом.

2. Порядок выполнения работы

Целью данной работы является изучение преобразования аналогового сигнала в цифровой и интегральной оценки возникающей при этом погрешности.

Этапы выполнения работы.

1. Измерение параметров процесса, заданного графиком в файле пакета AutoCAD.

2. Запись данных измерения в файл электронных таблиц Excel

3. Средствами пакета MatchCAD построить график дискретизированных значение P(t) и интегральным способом оценить его точность.

4. Построение полинома k –той степени и интегральная оценка точности его соответствия заданной функции U=f(t).

В файле пакета AutoCAD (Рuс0.dwg), дан график (рис.5) непрерывного анало-гового сигнала изменяющегося на интервале от 0. . .25.

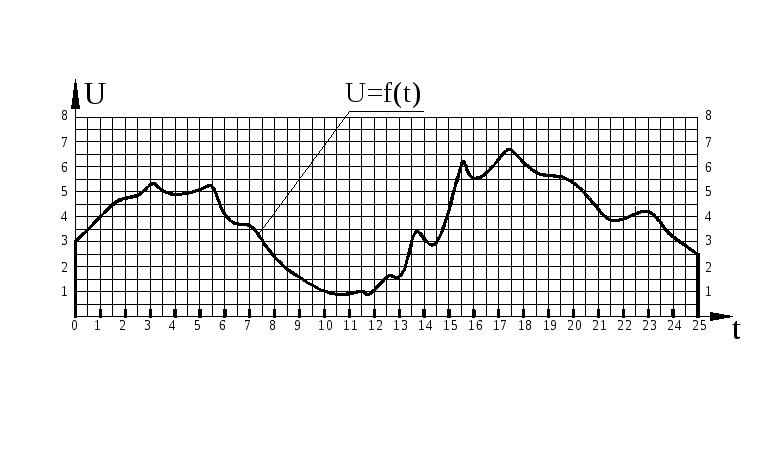
Рис. 5 График сигнала U=f(t).

График прочерчен полинией и начинается в точке (0, 3), а заканчивается в точке (25, 2.5) координатной системы AutoCAD - World. Вертикальные отрезки построенные в начальной и конечной точках графика дают возможность определить площадь, ограниченную кривой графика и горизонтальной координатной осью t (ось t совпадает с осью X, а ось U c осью Y координатной системы World), командой «AREA» (Площадь). Инициализировав команду и выбрав опцию «Object» выделяем заданную полиниеию, находим площадь S.

Необходимо выполнить дискретизацию непрерывного аналогового сигнала U=f(t) рядом значений U₁, U₂, U₃ .... измеренных в дискретные моменты времени t₀, 2t₀, 3t₀ . . . , где t₀=1 – период дискретизации.

Командой AutoCAD «ID» определяем значение функции в дискретные моменты времени t=1, 2, 3, … Данные записывает в файл Excel Рuс0.xls.

Долее работаем в среде пакета MathCAD (файл Puc0. mcd)

Переменной Р присваиваем значение двухстолбцовой матрицы элементы которой записаны в файле Excel Рuс0.xls.

Переменная x (столбец «А» файла Рuс0.xls) это последовательный ряд значений кратный периоду дискретизации t₀.

Переменная y (столбец «B» файла Рuс0.xls) это последовательный ряд значений функции U=f(t) полученной измерением заданного графика.

Погрешность дискретизации оцениваем интегральным методом, как разность площадей: площади функции ограниченной дискретизированной кривой и площади S полученной командой AutoCAD.

Значение оценивает в процентах точность соответствия ступенчатых значений P(t), кривой заданного графика.

Средствами пакета строим график (Puc.6, файл Puc0. mcd) , значения которой приближаются методом полиномиальной регрессии, к заданному графику. Это означает приближение данных U(t₀), U(2t₀), U(3t₀), . . . функцией в виде полинома степени k:

При k=1 полином является прямой линией, при k=2 - параболой, при k=3 кубической параболой и т. д.

Для построения регрессии полиномом k –той степени необходимо наличие, по крайней мере, k+1 точек данных

В MathCAD полиномиальная регрессия осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции.

- regress (х, у, k) - вектор коэффициентов для построения полиномиальиой регрессии данных;

- interp (s, x, у, t) - результат полиномиальной регрессии,

где:

s = regress (х, у, k);

х - вектор действительных данных аргумента, элементы которого. расположены в порядке возрастания;

у - вектор действительных данных значений того же размера;

k - степень полинома регрессии (целое положительное число);

t - значение аргумента полинома регрессии.

Числовые значения погрешности дискретизации W(t) можно получить, как абсолютное значение разности функций полиномиальной регрессии и функции дискретного ряда значений t

Значения погрешностей можно также получить путем трассировки графиков P2(t) и Fw(t) (Puc.7, файл Puc0. mcd)

Максимальную по модулю погрешность дискретизации определяем как разность ординат между построенной кривой и заданной. Такое действие может быть выполнено с помощью трассировки графиков или рассчитано автоматически с помощью программного сегмента.

Файл MathCAD созданный по типу Puc0. mcd и сохраненный в формате .rtf и отредактированный, является отчетом по данной работе.

Контрольные вопросы по выполнению работы

1. Характеристика центрального процессора.

2. Характеристика адресной памяти.

3. Характеристика стековой памяти.

4. Периферийные устройства. Общая характеристика.

5. Способы обмена информации между внешним устройством и ЭВМ.

Общая характеристика.

6. Асинхронная последовательная передача данных.

7. Дистанционная связь. Характеристика.

8. Программно-управляемая передача данных. Общая характеристика.

9. Синхронный и асинхронный обмен при программно-управляемой

передаче данных.

10. Обмен информацией по прерыванию.

11. Надежность работы ЭВМ и средства ее повышения.

12. Постоянные запоминающие устройства.

13. Внешние запоминающие устройства.

14. Аналогово-цифровые преобразователи