Энергия электрического поля.

Энергетический подход к рассмотрению взаимодействия электрических зарядов с одной стороны является весьма плодотворным по своим практическим применениям, а с другой, позволяет по-иному взглянуть на само электрическое поле как физическую реальность.

Энергия системы зарядов.

При элементарном перемещении зарядов в электрическом поле силы кулоновского взаимодействия совершают работу: , т.е. работа, производимая полем над электрическим зарядом, равна убыли потенциальной энергии этого заряда в рассматриваемом поле.

Для того, чтобы прийти к понятию энергии взаимодействия зарядов, рассмотрим сначала систему, состоящую из двух точечных зарядов 1 и 2. Найдем энергию взаимодействия зарядов. Пусть в рассматриваемом пространстве имеется неподвижный точечный заряд . Перенесем зарядиз бесконечности (где мы как обычно полагаем потенциал равным нулю) в точку, отстоящую на расстояниеот первого заряда, а затем проделаем то же самое с первым зарядом, предварительно зафиксировав положение заряда 2. Поскольку кулоновское поле – потенциальное, то совершаемые работы (в данном случае работы против сил поля) будут равны

.

Итак, получаем

,

где энергия взаимодействия точечных зарядов 1 и 2.

Или в симметричной относительно обоих зарядов записи:

.

Тогда потенциальная энергия системы зарядов может быть представлена в виде:

,

где потенциал, создаваемый всеми остальными зарядами системы в точке, где находитсяый заряд.

В случае непрерывного распределения зарядов эти формулы нетрудно.

Примеры:

а) Энергия уединенного проводника. Как обычно полагаем, что потенциал незаряженного проводника равен нулю (). Зарядим проводник, перенося на него заряд бесконечно малыми порциями, до значения. Сосчитаем работу, затраченную на сообщение проводнику заряда, т.е. его потенциальную энергию (потенциальную энергию взаимодействия находящихся на проводнике электрических зарядов). Потенциал уединенного проводника в каждый момент определяется соотношением, поэтому приращение его потенциальной энергии при увеличении заряда проводника насоставляет величину

.

Тогда потенциальная энергия уединенного проводника, заряженного до значения, равна

,

или, учитывая связь между зарядом, потенциалом и емкостью проводника, можем записать

.

б) Энергия конденсатора. Конденсатор – устройство, позволяющее накапливать электрическую энергию. Заряд конденсатора осуществляется путем переноса заряда от одной пластины к другой. При этом под зарядом конденсатора мы понимаем абсолютное значение заряда , находящегося на одной из его пластин (обкладок).

Если положить в выражении ()

,

где ипотенциалы обкладок, и использовать формулу (5.5) для электроемкости плоского конденсатора, положив в ней(воздушный конденсатор)

,

получим выражение для энергии заряженного конденсатора:

Последнее соотношение очень важно – оно определяет энергию конденсатора как энергию электрического поля , заключенного в пространстве между его обкладками. Наряду с энергией можно ввестиплотность энергии электрического поля конденсатора:

.

Энергия электрического поля.

Можно показать, что и в общем случае энергия произвольной системы электрических зарядов может быть выражена через характеристику самого электрического поля, его напряженность , создаваемого этой системой:

.

где интегрирование в правой части ведется по объему, где поле отлично от нуля.

. Энергия электрического поля в диэлектриках.

Энергия электростатического поля в диэлектрике выражается через векторы напряженности поля и электрической индукции:

,

а плотность энергии равна

.

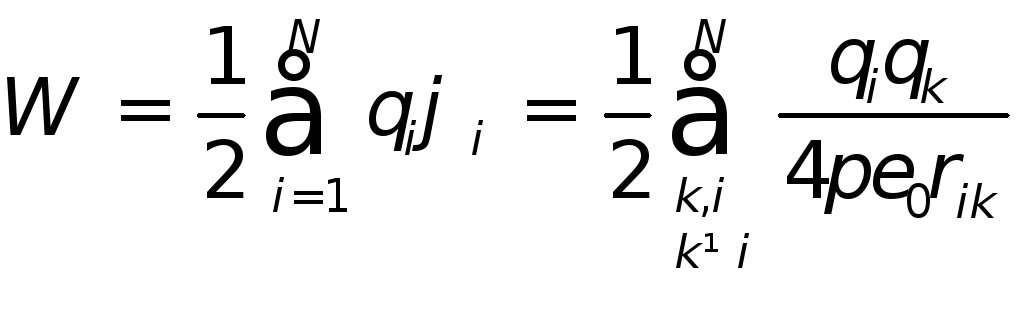23