11. .4. 2. 2. Представление стоячих волн.

Стоячие волны в натянутой струне или натянутом тросе удовлетворяют урав­нениям:

.

(11.30)

где — сила натяжения струны плот­ностью и поперечным сечением.

ДОКАЗАТЕЛЬСТВО. Определение стоячей волны требует выполнения ус­ловия . Ес­ли подставить это выражение в волновое уравнение натянутой струны, то получится дифференциальное урав­нение (11.30) для.

11. 4. 2. 3. Собственные частоты и ха­рактеристические длины волн.

Из диф­ференциального уравнения для и граничных условий:

.

(11.31)

получаются собственные круговые частоты сто­ячих волн в струне:

.

(11.32)

ДОКАЗАТЕЛЬСТВО. Общее реше­ние уравнения имеет вид. Поэтому граничные условия записы­ваются

.

Отсюда следует

Следовательно, вдоль длины струны должно размещаться целое число половин длины волны.

11. 4. 2. 4. Собственные колебания и формы колебаний.

Собственные коле­бания или характеристические стоячие волны в натянутой струне или натянутом тросе описываются формулой

.

(11.33)

Произвольные стоячие волны представ­ляют собой линейные суперпозиции соб­ственных колебаний:

.

(11.34)

Так как , то стоячие волны в струне можно представить также рядами Фурье по времени:

(11.35)

или рядом Фурье по ко­ординате:

.

(11.36)

11. 4. 2. 5. Фигуры Хладни.

Стоячие волны могут реализовываться не только в струне (одномерной структуре), но и в мембранах (двухмерные структуры) и объемных резонаторах (трехмерных структурах, примером которых может служить зал консерватории или концертный зал).

Собствен­ные колебания и спектр собственных час­тот даже произвольно натянутой тонкой мембраны могут быть очень сложными. Соб­ственные колебания мембраны можно сделать видимыми, если посыпать гори­зонтально натянутую мембрану мел­ким песком. При собственных колеба­ниях мембраны на ней существуют линии узлов, которые находятся в покое: =0. Мелкий песок благодаря собственным колебаниям перемещается по мембране, но остается лежать вдоль линий узлов, которые поэтому стано­вятся видимыми. (Места тела в которыхимеет максимальное значение называютсяпучностями). Получаемые таким об­разом линии названы фигурами Хладни — по имени Е. Хладни (1756—1824).

11. 5. Распространеиие волн в средах с дисперсией. Волновой пакет. Фазовая и групповая скорости.

Если возмущение (волна) распространяется в среде без изменения своей формы, то достаточно легко ответить на вопрос о том, с какой скоростью распространяется волна. Напомним, что понятие скорости возникло в механике для описания движения частицы (материальной точки). В волновом же движении происходит перенос состояния (т.е. значений поля) из одного места в другое. В общем случае понятие скорости неоднозначно. Так как при своем распространении волна взаимо­действует с веществом, то становится возможным искаже­ние формы возмущения. Такие среды называют средами с дисперсией.

В среде с дисперсией возмущение по мере распространения деформируется, и понятие скорости становится неопределенным. Такое волновое движение можно сравнить с движением тела, изменяющего свою форму. Для такого тела не существует однозначного понятия скорости: можно говорить о скорости движения его переднего края («фронта»), о скорости его центра тяжести и т.д.

Так же обстоит дело со скоростью волнового движения в диспергирующей среде. Поэтому приходится вводить ряд дополнительных понятий: скорость группы, скорость энергии, скорость фронта, скорость сигнала и т.д.

На практике всегда наблюдаются не монохроматическая волна более или менее сложный импульс или, как говорят, «волновой пакет», ограниченный в пространстве и во времени. При определенных условиях деформация («расплывание») волнового пакета происходит медленно и можно говорить о его скорости, рассматривая скорость какой-либо точки пакета, например, соответствующей максимальной амплитуде. На то, что скорость пакета будет отличаться от фазовой скорости любой из составляющих его монохроматических волн, впервые обратил внимание Стокс.

	Рассмотрим модулированную волну, возникающую в результате наложения двух монохроматических волн Одина­ковой амплитуды с близкими значениями длин волн и. На рисунке 11.4 показано относительно расположение (a) двух монохроматических волн разной длины и одинаковой амплитуды и (б) результат их суперпозиции. В результирующей волне максимумы амплитуды образу­ются в тех местах, куда обе волны приходят
Рисунок 11. 4.

в одинаковой фазе (там, где совпадают «горбы» волн).Там, где «горб» одной волны совпадает с впадиной другой (колебания происходят в противофазе), результирующая волна имеет нулевую амплитуду.

	Полученную картину можно рассматривать как последова­тель­ность отдельных «волновых групп». При каждая группа содержит большое число периодов. Если скорости склады­ваемых волн одинаковы, то результирующая модулирован­ная волна распространяется с той же скоростью, не изменяя своей формы.
Рисунок 11. 5.

При наличии дисперсии монохроматические составляющие имеют несколько различающиеся фазовые скорости и. Поэтому взаимное расположение их горбов и впадин меняется с течением времени. Общий вид результирующей волны остается прежним, однако центры отдельных групп с течением времени смещаются относительно горбов и впадин складываемых исходных волн, т.е. движутся с иной скоростью, нежели складываемые монохроматические волны (см. рис. 11.5).

Скорость движения центров этих волн называют групповой скоростью. Найдем связь между фазовой скоростью движения монохромати­ческой волны и групповой скоростью. Будем для определен­ности считать, что скорость монохро­матических волн растет с увеличе­нием длины волны (нормальная дисперсия). В области нормальной дисперсии большей скоростью будет обладать волна, имеющая большую длину. Поэтому, как показано на рисунке 11. 6, “нижняя” волна, имеющая длину , обгоняет “верхнюю” волну длиной.

Пусть в некоторый момент времени совпадают горбы иэтих волн, т.е. центр группы волн приходится на точку .

	Через некоторое время горбобгонит горб, но совпадут горбыи. Это значит, что центр группы волн за это время сместился назад на расстояние, равное длине волны, и совпадает теперь с точкой. Т.о., находим, что скорость центра группы меньше фазовой скоростиверхней волны на величину:
Рисунок 11.6.
.		(11.37)

Время , в течение которого горб«догоняет» горб, определяется как.

Если группа образована монохроматическими волнами, длины которых отличаются на малую величину, то устремляя в пределе получаем выражение для групповой скорости в виде:

.

(11.38)

Полученное выражение носит название формулы Рэлея.

При отсутствии дисперсии групповая скорость совпадает с фазовой. При нормальной дисперсии, поэтому групповая скорость меньше фазовой:. В области аномальной дисперсии, и формула Рэлея дает.

Формула Рэлея справедлива не только для скорости перемещения бесконечной череды волновых групп, образующихся при сложении двух монохроматических волн. При определенных условиях она характеризует также скорость движения центра одиночного волнового пакета, образованного непрерывным набором монохроматических составляющих. Эти условия касаются как самого волнового возмущения, так и свойств среды, в которой оно распространяется – для монохроматических волн, входящих в состав рассматриваемого возмущения и имеющих длины в интервале , фазовая скоростькаждой волны в среде должна в хорошем приближении представлять линейную функцию длины волны. Другими словами, групповая скорость, определяемая формулой Рэлея, в пределах заданного интервала длин волн должна быть постоянной.

Простой графический способ нахождения групповой скорости по кривой зависимости скорости волны от её длины был предложен Эренфестом.

Отрезок, отсекаемый на оси ординат (см. рис. 11 7) касательной в точке к кривой, равен, т.е. значению групповой скорости при данной длине волны.

	Приведенный рисунок хорошо иллюстрирует смысл сформули­рован­ного условия: если любая огибающая суммы двух произ­вольных монохроматических состав­ля­ющих из интервала перемещается с одной и той же скоростью, то и весь импульс будет перемещаться с этой же скоростью, не изменяя своей формы, т.е. не «расплываясь».
Рисунок 11. 7.

Часто бывает удобно использовать для записи групповой скорости вместо длины волны волновое число (модуль волнового вектора):

.

(11.39)

Существуют и другие эквивалентные формулы для преставления групповой скорости – через частоту как функцию волнового числа

: ;

(11.40)

или через показатель преломления (величину, равную отношению фазовых скоростей монохроматической волны в двух средах), заданный как функция частоты

: .

(11.41)

В области аномальной дисперсии групповая скорость, определяемая по формуле Рэлея, оказывается больше . Это связано с тем, чтоизменение показателя преломления вблизи собственной частоты атомных осцилляторовпроисходит нелинейно, поэтому импульс по мере распространения неизбежно деформируется. В таких условиях на конечном интервале расстояний максимум огибающей может перемещаться со скоростью, превосходящей скорость света в вакууме (или даже с отрицательной скоростью), но этот результат не противоречит постулату теории относительности, т.к. эта скорость связана с “внутренней” перестройкой импульса и не может быть использована для передачи сигнала.
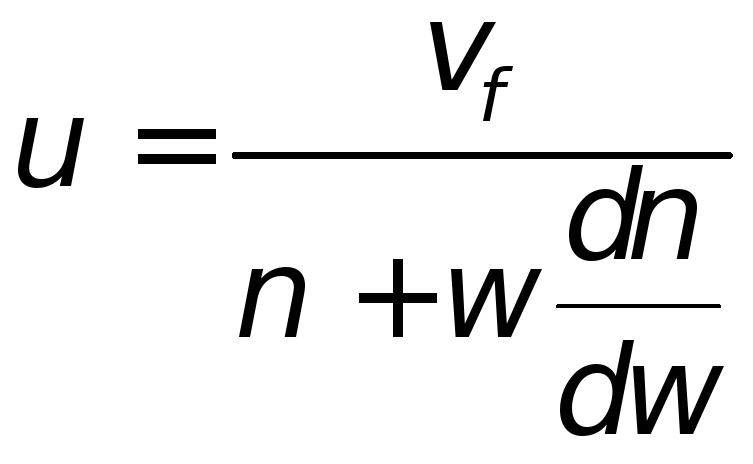