11. 3. Звук.

Скорость звука. Ниже в таблице приводятся значения скорости звука (продольных упругих волн) в различных средах, находящихся под атмосферным давлением при температуре 20 °С:

Газ	, м/с		Конденсированная среда	, м/с
Двуокись углерода	266		Медь	5000
Кислород	326		Алюминий	6400
Воздух (0 °С)	331		Алмаз	17 500
Азот	349		Ацетон	1190
Гелий	1010		Бензол	1324
Водород	1324		Вода	1500

Интенсивность звука равна среднему зна­чению, по времени от вектора Умова – вектора мгновенной плотности потока энергии. Для плос­кой гармонической звуковой волны:

(11.23)

Уровень звука и громкость. Уровнем звука, или уровнем звуковой мощности называют величину:

(11.24)

где .

Единицей уровня звука является де­цибел (дБ). Субъектив­но воспринимаемая ухом громкость связана, согласно В. Веберу (1804— 1891) и Г. Т. Фехнеру (1801—1887), с интенсивностью звука соотношением

(11.25)

где — порог слышимости. Поэтому громкость есть линейная функция уров­ня звука. Для частоты = 1000 Гц обе величины произвольно

	приравнены друг другу. Для других частот они разли­чаются из-за зависящей от частоты чув­ствительности уха. Определенную таким образом единицу громкости называют фоном. Связь меж­ду интенсивностью звука, уровнем звука и громкостью представлена на рис. 11.3. Порог слышимости соответствует громкости, равной 0 фонов, а болевой порог – громкости в 120 фонов.
Рисунок 11. 3.

11. 4. Интерференция волн

11. 4. 1. Принцип суперпоиции. Интерференция.

Принцип суперпозиции. Принцип суперпозиции утверждает, что два однотипных волновых поля и налагаются аддитив­но:

.

(11.26)

Этот принцип эквивалентен принципу невозмущенного наложения, согласно ко­торому любое волновое поле распростра­няется так, как будто другие однотип­ные волновые поля отсутствуют.

Вооб­ще говоря, принцип суперпозиции не выполняется, если в среде, в которой рас­пространяется волна, возникают нели­нейные эффекты. В этом случае прин­цип суперпозиции применим лишь для волн с малыми амплитудами. Для по­перечных волн он выполняется только для компонент волновых полей с оди­наковым направлением поляризации.

Возникающее при наложении однотип­ных волн явление зависимости интен­сивности от фазы, координаты или на­правления называют интерференцией. Здесь рассмотрим интерференцию, возникающую результате аддитивного наложения двух одинаково направленных гармони­ческих волн с различными фазами и или (и) разностью хода:

.

(11.27)

Принцип суперпозиции дает для пол­ной волны:

.

(11.28)

Интенсивность этой волны вычисляется как среднее значение по времени:

.

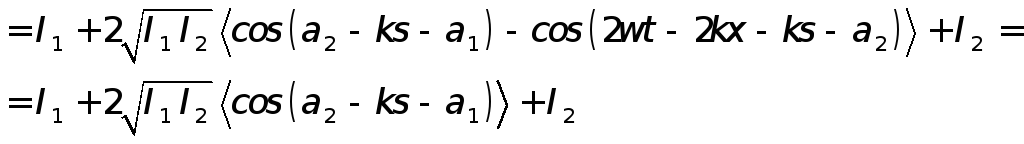Или

.

(11.29)

Следовательно, интерференция приводит к перераспределению интенсивности колебаний в пространстве.

11. 4. 2. Стоячие волны

11. 4. 2. 1. Основные положения.

Стоячие волны представляют собой колебания непре­рывной среды или пространственно-пе­риодической структуры. Для каждой возможной частоты колебаний среда во всех точках колеблется в одной и той же фазе. Это означает, что колебания среды находятся в фазе или в противофазе.

Стоячие волны могут быть пред­ставлены наложением бегущих волн.

Граничные условия и собственные частоты. Стоя­чие волны существуют лишь при определенных частотах, называемых собственными частотами. Эти частоты определяются граничными условиями, которым удовлетворяет среда или про­странственно-периодическая структура. Каждой собственной частоте стоячей волны отвечает определенная простран­ственная картина колебаний, которая в частных случаях может быть описана с помощью характеристической длины волны. По этим причинам стоячие волны можно понимать как собственные колеба­ния систем с бесконечным числом степе­ней свободы.

Классические стоячие волны. Классическими стоячими волнами являются колебания натянутой струны (скрипка, фортепиано, арфа), натянутой мембраны (литавры, громко­говоритель, микрофон), воздуха в зву­ковых резонаторах (органные трубы, флейты) и электромагнитные колебания в микроволновых и лазерных резонато­рах.