3.3.3 Определение расчетной несущей способности одного «среза» нагеля

Для определения несущей способности одного среза нагеля следует рассмотреть напряженное состояние нагельного соединения. Действующие в соединяемых элементах усилия стремятся сдвинуть их относительно друг друга. Нагель, препятствуя этому, изгибается. Изгиб нагеля зависит от жесткости самого нагеля и смятия древесины нагельного гнезда. Нагель можно рассматривать как балку, лежащую на сплошном упругопластическом основании - древесине нагельного гнезда. Напряжения смятия в древесине по длине нагеля распределены неравномерно. Эта неравномерность тем значительнее, чем меньше жесткость нагеля (рис.3.19). Неравномерно также рас­пределение сминающих напряжений по контуру нагельного гнезда (рис. 3.20).

Равнодействующие радиальных напряжений, расположенных выше и ниже продольной оси х-х, направлены по углом к этой оси и, будучи разложены, дают две составляющие - продольную Т и поперечнуюПродоль­ная составляющая Т = Т_н+ Т_в вызывает появление напряжений скалывания по площадкам а-а и а'-а'. Поперечные составляющие

и стремятся расколоть деревянный элемент по линии б-б. Еще более сложно напряженно-деформированное состояние нагельного соединения деревянных эле­ментов, расположенных под различными углами.

Несущая способность нагеля из условий скалывания и раскалывания древесины соединяемых элементов главным образом зависит от расстанов­ки нагелей. Минимальное расстояние между нагелями назначают таким об­разом, чтобы в соединении несущая способность соединяемых деревянных элементов по скалыванию и раскалыванию заведомо превышала несущую способность нагеля по его изгибу и смятию древесины нагельного гнезда.

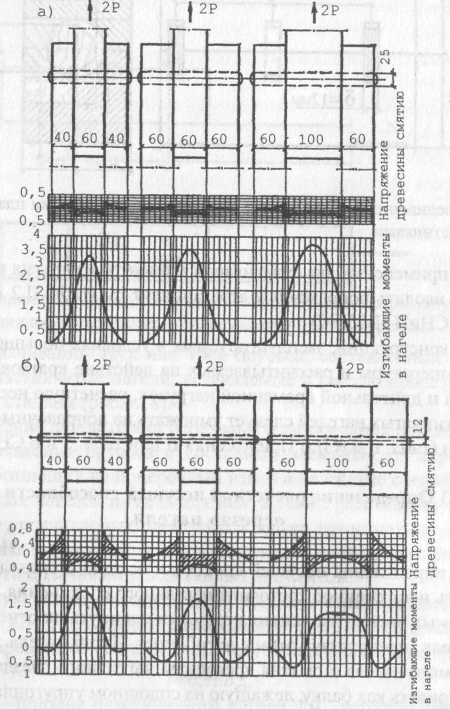
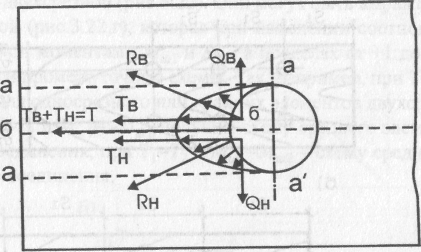
Рис 3.20. Эпюры радиальных напряжений смятия древесины нагельного гнезда

Рис. 3.19. Эпюры напряжений древесины нагельного гнезда смятия и изгибающих

моментов в нагеле: а - при диаметре нагеля 25 мм; б - то же, 12 мм

Несущая способность нагеля из условий скалывания и раскалывания древесины соединяемых элементов главным образом зависит от расстановки нагелей. Минимальное расстояние между нагелями назначают таким образом, чтобы в соединении несущая способность соединяемых деревянных элементов по скалыванию и раскалыванию заведомо превышала несущую способность нагеля по его изгибу и смятию древесины нагельного гнезда.

Минимальные расстояния между осями нагелей принято выражать в диаметрах нагеля. Они определяются видом нагелей и толщиной соединяемых элементов. Расстановка нагелей в соединениях может быть прямой или в шахматном порядке (рис.3.21). В табл. 3.4 приведены рекомендуемые СНиП П-25-80121 минимальные расстояния между цилиндрическими наге­лями.

Таблица 3.4.

Минимальные расстояния между нагелями

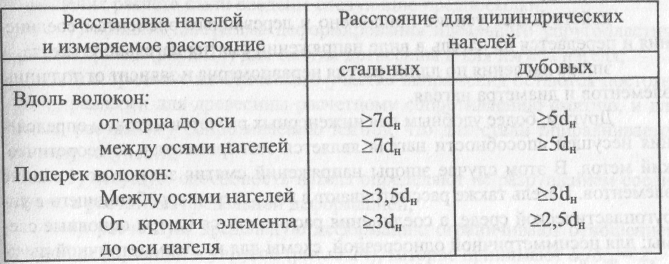
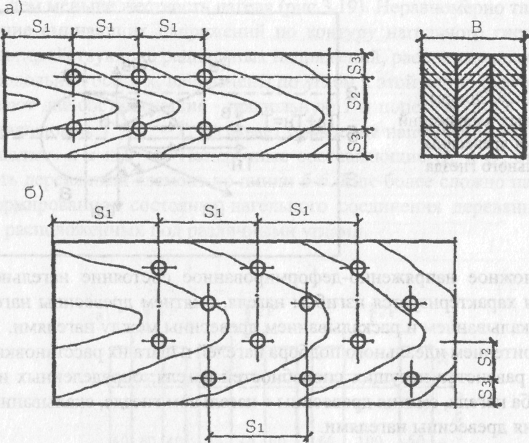
Рис. 3.21. Расстановка нагелей: а - прямая; б - в шахматном порядке

При соблюдении расстановки нагелей расчетная несущая способность одного нагеля Т_н определяется только из условий изгиба нагеля и смятия древесины нагельного гнезда в обоих прилегающих к шву элементах. Теоретически нагель, как уже указывалось, рассматривают как балку, лежащую на упругом или упругопластическом основании, за которое принимают древесину соединяемых элементов. В основу расчета могут быть поло­жены различные теоретические предпосылки, характеризующие само основание, режимы нагружения, особенности деформирования во времени и другие факторы. Однако расчет нагеля сложнее, чем расчет балки, лежащей на сплошном основании. Сложность задачи состоит в следующем:

основание, на которое опирается нагель, разделено на части, например, в симметричном двухсрезном соединении имеются две крайние и одна средняя часть;

действующее усилие приложено к деревянным элементам соединения и передается на нагель в виде напряжений смятия нагельного гнезда;

эпюра давления по длине нагеля неравномерна и зависит от толщины элементов и диаметра нагеля.

Другим, более удобным для инженерных расчетов методом определения несущей способности нагеля является экспериментально-теоретический метод. В этом случае эпюры напряжений смятия задают по толщине элементов. Нагель также рассматривают в виде стержня, работающего в упругопластической среде, а соединения расчленяются на три основные схемы: для несимметричной односрезной, схемы для кососимметричной двух срезной и симметричной двухсрезной (рис.3.22). Они могут быть выражены одной обобщенной схемой (рис.3.22,г), которая при изменении соотношений между силами Т₁ и Т₂ и моментами М_ш1 и М_ш2 в пределах от +1 до -1 охватывает все основные и промежуточные схемы. Так, например, при Т1+0 и М_ш1+0 получим схему для односрезного или крайних элементов двухсрез-ных соединений; при Т_}— -Т₂ и М_ш1= -М_ш2 получим схему среднего элемента кососимметричного соединения; при Т₁=Т₂ и М_ш1=М_ш2 - схему среднего шемента симметричного соединения.

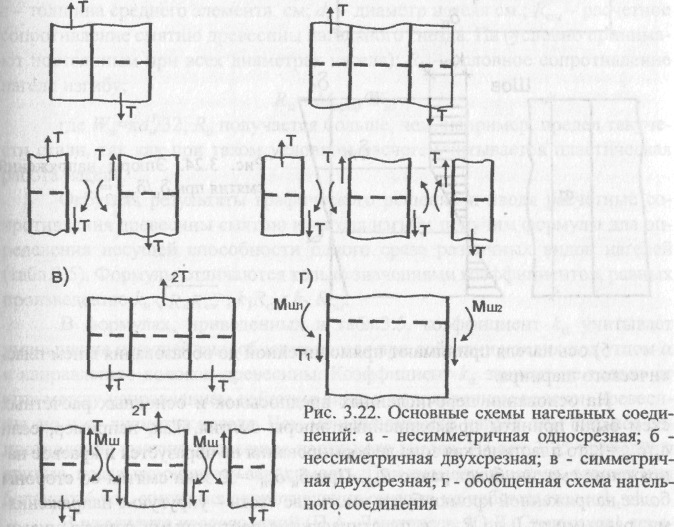
При разработке этого метода (автор - д-р техн.наук В.М.Коченов) для упрощения расчета были введены следующие предпосылки:

1. принята диаграмма деформирования идеального упругопластичного материала (рис.3.23) для смятия древесины и для изгиба нагеля;

2. в пределах пластического участка напряжения остаются постоянными, равными для древесины расчетному сопротивлению смятию, и для нагеля расчетному сопротивлению изгибу, что для стали приравнивается пределу текучести;

3. несущую способность нагеля определяют не разрушением соединения, а расчетной предельной деформацией;

4) расчетную предельную деформацию ограничивают отношением полной деформации к упругой (рис. 3.24), которое принимают