2 Решение дифференциального уравнения теплопроводности для неограниченного цилиндра

Если длина l цилиндра значительно больше его диаметра 2R (l/2R > 3), то его можно уподобить неограниченному цилиндру, у которого длина бесконечно велика по сравнению с его диаметром.

Если теплообмен между поверхностью цилиндра и окружающими телами происходит одинаково по всей поверхности, то температура его будет зависеть только от времени и радиуса (симметричная задача), т.е. задача сводится к следующему:

Дан неограниченный цилиндр при некотором заданном радиальном распределении температур в виде функции Т_о = f(r). В начальный момент времени поверхность цилиндра мгновенно нагревается до некоторой температуры Т_с, которая поддерживается постоянной на протяжение всего процесса нагрева (охлаждения). Необходимо найти распределение температуры внутри цилиндра в любой момент времени.

Дифференциальное уравнение теплопроводности в данном случае имеет вид (1.2).

Решение задачи при краевых условиях

; (2.1)

(2.2)

(последнее из которых означает, что температура на оси цилиндра на протяжении всего процесса теплообмена должна быть конечной) имеет вид:

, (2.3)

где

_n – корни характеристического уравнения :

- функция Бесселя первого рода нулевого порядка [1];

- число Фурье.

Из анализа решения (2.3) следует, что ряд быстро сходится, так как и с увеличением_n А_n уменьшается, а также резко уменьшается экспоненциальная функция . Поэтому, если исключить из рассмотрения малые значенияFo < 0,3, то можно ограничиться одним членом ряда (2.3) и расчетная формула приобретает простой вид

. (2.4)

Для малых чисел Fo (малых промежутков времени) можно получить приближенное решение в ином виде:

(2.5)

Функции erfc(х) и ierfc(х) табулированы [1].

Для r = 0

, (2.6)

где K_1/4 – модифицированная функция Бесселя второго рода

порядка 1/4 [1].

При аргументе больше 2, K_1/4 можно определять по формуле:

При вычислении достаточно удержать 3 члена ряда.

3 Решение дифференциального уравнения теплопроводности для неограниченной

Рисунок 2

пластины

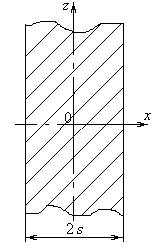
Неограниченная пластина представляет собой тело, ограниченное двумя плоскостями.

Изменение температуры происходит только в одном направлении х, в двух других направлениях температура неизменна (одномерная задача) (рис. 2).

Условие задачи математически можно сформулировать в виде дифференциального уравнения со следующими краевыми условиями:

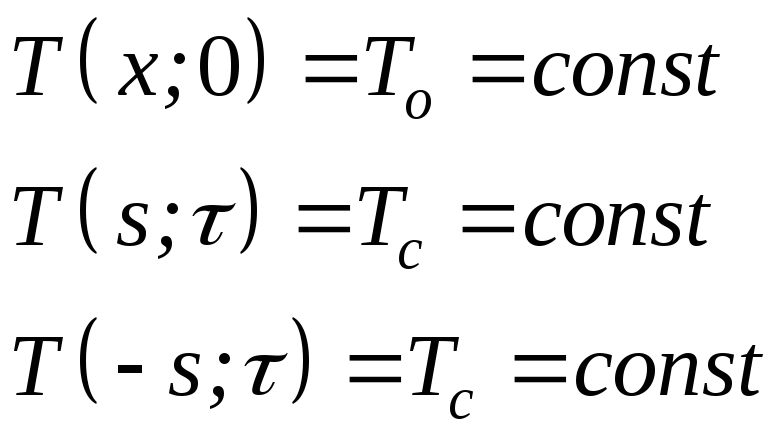(3.1)

решение задачи имеет вид:

, (3.2)

где

т.е. относительная температура является функцией относительной координаты и числа Фурье

.

При малых числах Fo (Fo < 0,3) решение имеет вид

. (3.3)

Для случая Fo > 0,3

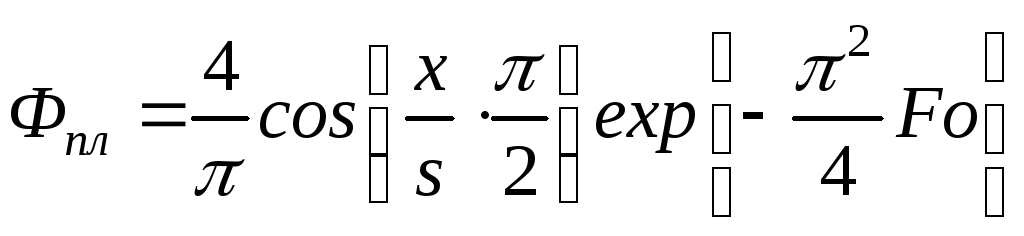. (3.4)

все функции, используемые в решениях (2.3)-(3.4) табулированы [1].

Зная решение дифференциального уравнения теплопроводности для бесконечного цилиндра и пластины (2.3)-(3.4), используя (2.1) можно получить решение для цилиндра конечной длины. Например, для определения температуры в точках, указанных на рис. 1, нужно записать уравнения:

;

и т.д.

На практике мы очень часто сталкиваемся с задачами, когда при постоянной температуре поверхности в теле уже имеется некоторое распределение температур. В случае отличия начального распределения температуры от равномерного, формулами (2.3)-(3.4) пользоваться нельзя. нужно пользоваться такими формулами:

– для пластины бесконечной длины

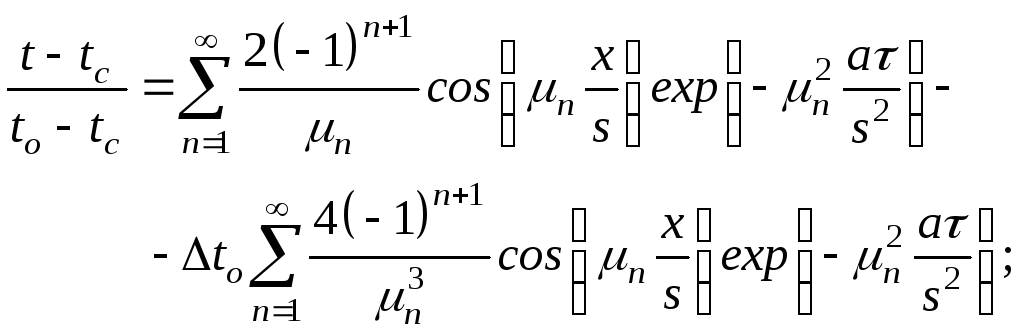(3.5)

– для цилиндра бесконечной длины

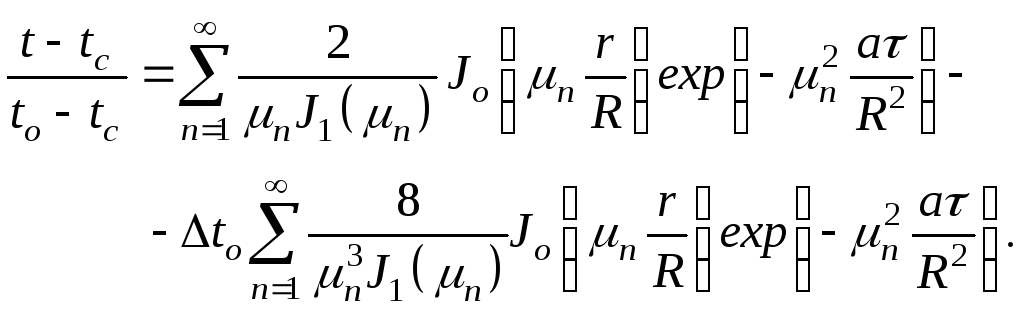(3.6)

где t_о – разница между температурой центра и поверхности

образца в начальный момент времени;

J₁ – функция бесселя первого рода первого порядка [1]

решения (3.5) и (3.6) предполагают, что начальное распределение температуры описывается квадратичной параболой.

Отношение разности температур поверхности и центра тела в процессе нагрева t к начальной разности этих температур t_о называется степенью выравнивания температур  = t/t_о.

Степень выравнивания температур является функцией числа Фурье и для тел различной формы ее можно определить по графику (рис. 1, приложение Б).