3. Проверочный расчет

Проверочный расчет на усталость по контактным напряжениям выполняется по формуле 9.42 [1]:

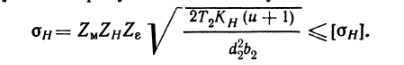
Коэффициенты:

- коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес - Zм = (275 Н/мм²)^1/2 ;

- безразмерный коэффициент, учитывающий суммарную длинуконтактных линий - Zε = 0,79;

- безразмерный коэффициент, учитывающий форму сопряженных поверхностей зубьев - Zн = 1,77 соs β

- коэффициент, учитывающий распределение нагрузки по поверхности зубьев - К_н = 1,17

Полученное контактное напряжение должно быть меньше или равно допустимому контактному напряжению, т.е. должно выполняться условие: σ_н≤ [σ_н], при котором обеспечивается прочность.

Определяем окружную скорость по формуле:

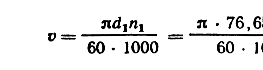
По таблице 9.9 [1] назначаем 8-ю степень точности передачи.

Пример 2 расчета одноступенчатого цилиндрического редуктора с косозубым зацеплением.

Рассчитать зубчатую передачу редуктора по данным примера 1. Вид зацепления зубьев – косозубое.

Расчет косозубой передачи проводится подобно расчету прямозубой передаче. Но есть некоторые изменения.

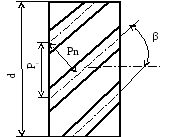
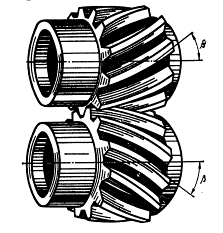
а) б)

Рис.3. а - косозубые колеса в зацеплении б - схематическое изображение косозубого колеса

1. Проектный расчет

В колесах с косым зубом различают окружной шаг р_t, который измеряется параллельно торцу колеса, и нормальный шагp_n, измеряемый в нормальном к направлению зуба сечении.

p_{n =} р_t cosβ,

где β – угол наклона линии зуба. Во избежание больших осевых усилий принимают β = 8⁰…15⁰(редко 20⁰).

Аналогично связаны между собой нормальный m_nи окружной модули m_t.:

m_n = m_t cosβ

По стандарту обычно выравнивают нормальный модуль.

1. Определение геометрических параметров зубчатой передачи.

Согласно правилам проектирования, вычисляем ориентировочное значение нормального модуля:

m_n = (0,01…0,02)a= (0,01…0,02)280 = 2,8…5,6мм.

По таблице стандартных значений модулей (табл.9.1[1]) принимается наименьшиймодуль из выбранного интервала (в отличие от прямозубого зацепления).

Принимаем среднее значение угла наклона зубьев =15⁰

Рассчитываем суммарное число зубьев ([1], формула 9.4):

180,3180;

числа зубьев шестерни и колеса находим решением системы уравнений:

;

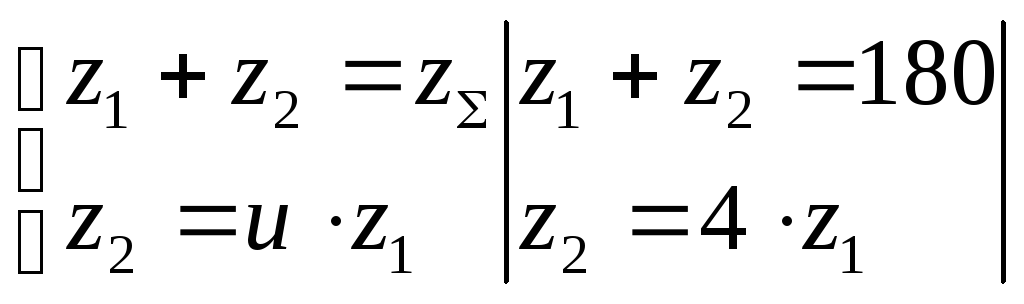z₁= 180/(1+4)≈36;

z₂=180 – 36= 144;

проверяем передаточное число:

;

погрешность передаточного числа:

0%,

что соответствует условиям ([1], табл.9.2 п.3 примечаний).

Определяем окончательно значение угла наклона зубьев:

15^о35′45′′. или

cosβ = (z₁+z₂) m_n/ 2а = 0,9643 →β = 15^о35′85′′

Торцевой модуль:

3,111 мм.

Делительные диаметры:

d₁ =m_tz₁=m_nz₁/ cosβ= 3,11136= 111,996 мм;

d₂ =m_tz₂=m_nz₂/cosβ= 3,111144= 447,984 мм.

Проверка межосевого расстояния:

279,99 мм.

Полученные геометрические параметры косозубой передачи заносим в таблицу 3.1.

Таблица 1.1. Геометрические размеры цилиндрической зубчатой передачи

Название	Межо севое расстояние а, мм	Модуль m, мм	Число зубьев z	Угол наклона зубьев, 0	Ши рина зубчатого венца b, мм	Диаметры, мм
						d	dа	df
Шестерня	280	3	36	15о35′45′′	240	111,996	117,996	119,496
Колесо			144		230	447,984	453,984	455,484