2. Лабораторная работа «Анализ устойчивости электрической системы при больших возмущениях»

2.1. Объект исследования и цель работы

Объектом исследования в настоящей лабораторной работе является простейшая электроэнергетическая система, состоящая из удаленной электрической станции, соединенной линией электропередачи с мощной приемной системой. Станция и система представлены на схеме (рисунок 2.1) эквивалентными генераторами G1 иG2. К шинам станции и приемной системы может быть подключена одна из нагрузок Н1 — Н4. Линия электропередачи состоит из двух цепей (W1 иW2), коммутируемых выключателямиQ1,Q2,Q3,Q4. В одной из точек К1 — К7 возникает короткое замыкание (КЗ).

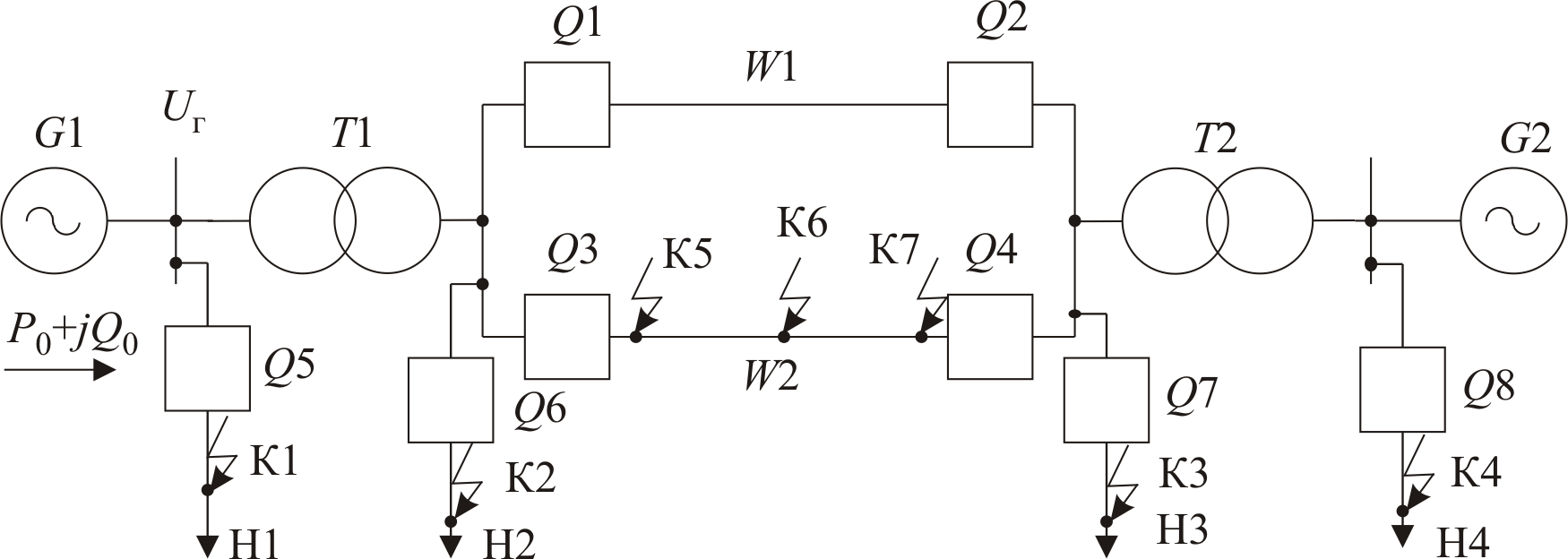
Рисунок 2.1 — Исследуемая система

Цель работы состоит в изучении методов анализа динамической устойчивости электрической системы с использованием способа площадей, определения предельного угла и времени отключения КЗ.

2.2. Основные теоретические положения

При возникновении КЗ происходит уменьшение электромагнитной мощности, отдаваемой генератором G1 в систему, при сохранении неизменной мощности турбины. В результате этого, возникает небаланс механического и электромагнитного моментов генератора и начинает увеличиваться скорость вращения его ротора. Если своевременно не отключит КЗ, то синхронная работа генератора и сети нарушиться.

Способ площадей позволяет определить размах колебаний ротора при отклонениях его от положения равновесия и найти тот предельный угол отключения поврежденного элемента, при котором может быть сохранена устойчивая работа генератора.

Предельный угол отключения может быть найден из условия равенства площадок ускорения и торможения в системе «генератор - шины подстанции»:

,

(2.1)

где — величина активной мощности, проходящей через рассматриваемое сечение, отн. ед.;

и— максимальные значения мощностей, определенные соответственно по характеристикам аварийного и послеаварийного режимов, отн. ед.;

— начальное значение угла, рад;

— критический угол, рад, определяемый как

.

(2.2)

При определении предельного угла отключения трехфазного КЗ вблизи шин . В остальных случаях (трехфазное КЗ на линии, несимметричные КЗ в любой точке) величинадолжна быть рассчитана на основании соответствующей схемы замещения, составленной для аварийного режима.

Метод площадей позволяет определить предельный угол отключения КЗ , однако для практического применения необходимо знать предельное время отключения. Перейти от предельного угла отключения к предельному времени отключения можно, имея зависимость δ=f(t), которую можно получить, решив дифференциальное уравнение движения ротора синхронного генератора. Однако это уравнение в большинстве случаев не имеет аналитического решения и может быть решено только с помощью численных методов.

При трехфазном КЗ на шинах подстанции, в начале или конце двухцепной линии, в любой точке одноцепной линии, разрыве передачи электрической мощности электромагнитная мощность падает до нуля (). Движение ротора генератора происходит только под действием механического момента турбины без отдачи генератором мощности в сеть. В этом случае вся мощность турбины идет на ускорение ротора генератора и уравнение его движения принимает вид

.

(2.3)

Решив уравнение (2.3), получаем

,

(2.4)

где — постоянная инерции, рад,

откуда

,

(2.5)

где время выражается в относительных единицах (радианах).

Выражение (2.5) дает возможность перейти от значений предельного угла отключения КЗ к значениям предельного времени отключения КЗ.

В случаях КЗ на одной из двухцепных линий (кроме КЗ в начале или конце линии) и несимметричных КЗ уравнение движения генератора можно записать как

.

(2.6)

Интегрируя уравнение (2.6), можно получить зависимость δ(t), с помощью которой возможен переход от предельного угла отключения к предельному времени отключения.

Для численного интегрирования уравнения (2.6) можно использовать метод последовательных интервалов.

При этом весь процесс разбивается на малые интервалы (обычно принимают=0,02…0,05 с или меньшие значения).

Для первого интервала приращение угла :

,

(2.7)

где — избыточная мощность в начале первого интервала, отн. ед. ();

— электромагнитная мощность генератора в начале первого интервала, отн. ед.;

,

(2.8)

где — синхронная скорость, рад/с.

Величина интервала задается в секундах, а значение углабудет получено в радианах.

Для последующих интервалов может быть использовано выражение

,

(2.9)

где — приращение угланаn-ом интервале, рад;

— приращение углана предыдущем интервале, рад;

— избыточная мощность в началеn-го интервала, отн. ед.

Полученная зависимость используется для определения предельного времени отключенияна основании значения предельного угла отключения.
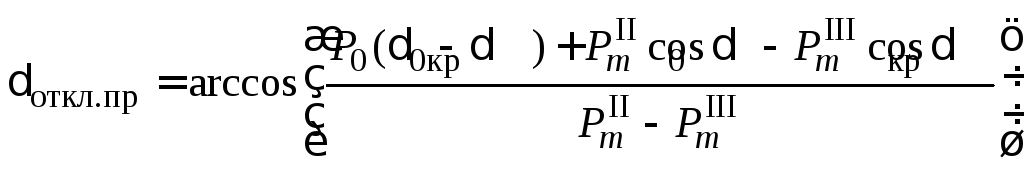