Умова міцності і умова жорсткості при крученні.

Для простого прямокутного перерізу:

–умова міцності.

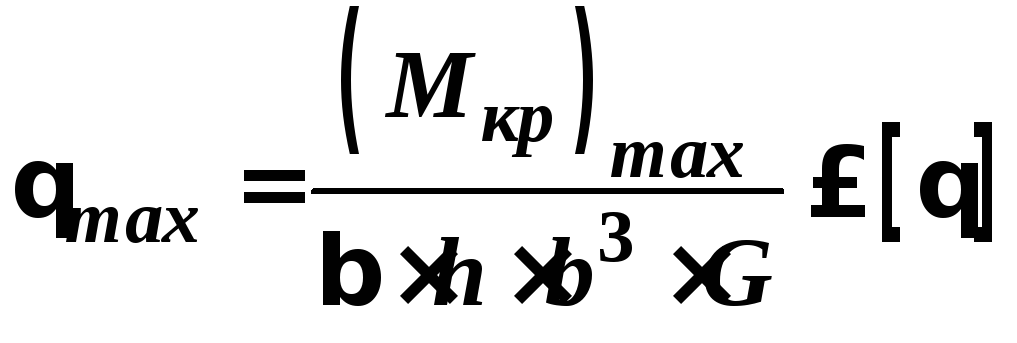–умова жорсткості.

Для складеного перерізу (складеного із простих прямокутників) умова міцності і умова жорсткості будуть:

, де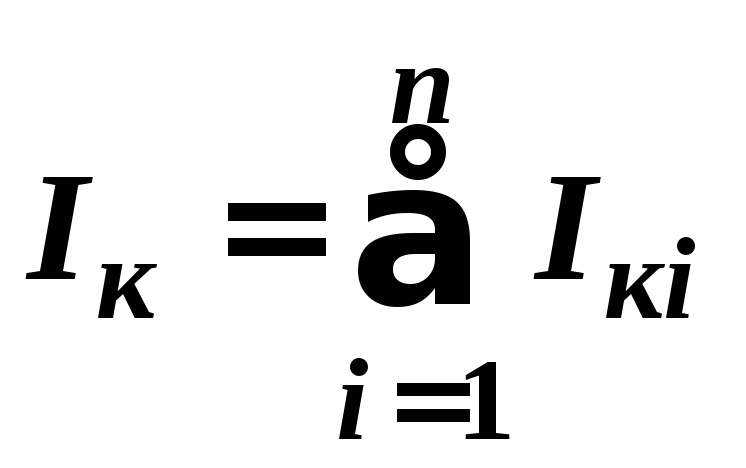

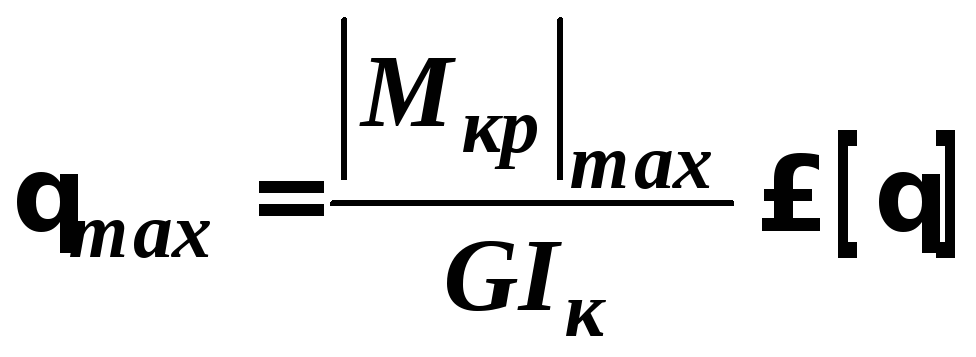–умова жорсткості.

Для прямокутників у яких відношення сторони

Кручення тонкостінних стержнів і профілів.

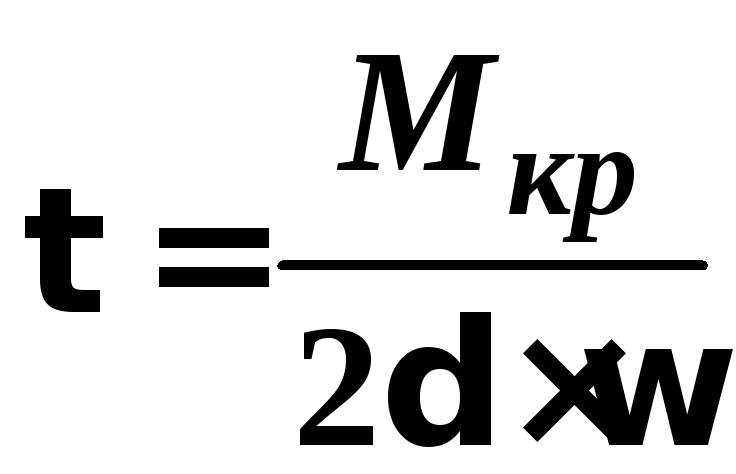–формула Бредта

для закритих профілів.

–крутний момент в перерізі, що розглядається по довжині стержня і береться з епюри.

–товщина стінки контуру, визначається в точці, де розраховуються дотичні напруження.

–площа поперечного перерізу контуру, що обмежена середньою лінією товщини контуру.

–формула для визначення максимального кута

закручування для закритих профілів.

– формула для визначення відносного кута закручення

закритих профілів.

де: – довжина відрізка стержня, що розглядається

–довжина середньої лінії контуру.

Ці формули застосовують тільки при .

Приклад:

Дано:

;;;;

і;.

Сталь.

Знайти:

;.

; 

Для тонкостінних відкритих профілів, виходячи з того, що будемо мати, що:

, де

для  ;  ; ð ; ð

Відтак позначаючи товщину стінки тонкостінного відкритого профілю через (), а довжину його через, момент інерції запишемо так:,

а залежність що визначає мах дотичні напруження в профілі, що має найбільшу товщину : .

Розрахунок циліндричних гвинтових пружин з малим кутом нахилу.

Припустимо, що пружина з середнім діаметром має– витків, розтягується силою. Для того, щоб оцінити міцність пружини проведемо перерізі розглянемо рівновагу відсіченої частини.

–дотичні напруження від зсуву.

–дотичні напруження від кручення.

Як бачимо, напруження від зсуву і від кручення в т.внутрішнього радіусу співпадають за напрямком. Відтак:



–умова міцності.

Якщо пружина із тонкої проводки має досить великий діаметр в порівнянні із товщиною дроту, то добавкою за рахунок сил зсуву нехтують і максимальне дотичне напруження: .

Робота, що виконує пружина при навантаженні дорівнює потенційній енергії.

– робота пружини

потенційна енергія

пружини за рахунок

тільки .

де, – усадка пружини,

– крутний момент,

– повний кут повороту.

Тоді робота на ділянці пропорційності буде дорівнювати добутку сили напереміщення.

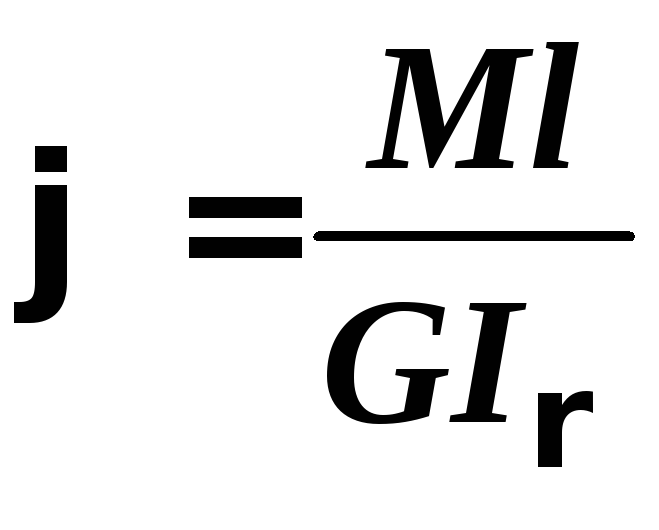З другої сторони: , а, де– довжина одного витка, а довжина всієї пружини:, де– число витків.

Тоді: 

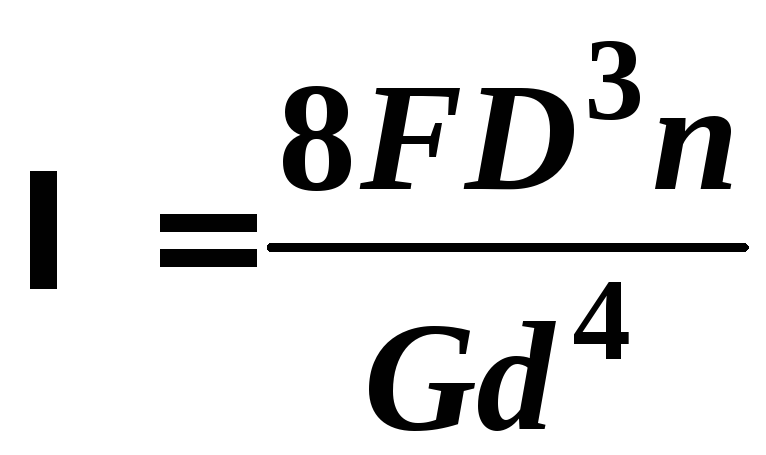–усадка пружини.

де, – сила, що розтягує чи стискає пружину;

–середній діаметр пружини;

–число витків;

–модуль пружності при зсуві;

–діаметр проволоки пружини.

Знаючи можна визначити об'єм пружини, а відповідно і вибрати товщину проволоки, та число витків і радіус чи діаметр пружини.

, де – енергія, що поглинається пружиною.

.