Приклад.

Дано:

кH; кH; кH/м.

Визначити: величину дотичних напружень в защемленні балки, що має трикутний поперечний переріз, в точці , яка знаходиться на відстаніперерізу з розмірамисм;см.

; (МПа)

Д.з. визначити -ні напруження в т.

Епюри розподілу дотичних напружень по висоті перерізу для різних його форм

Використовуючи формулу Журавського будемо вважати, що поперечна сила задана і, що вона. додатна.

1. Тоді для прямокутного перерізу:

, де .

, т.як

Розглянемо довільний шар на відстані "" і розрахуємо дотичні напруження в цих точках на цьому рівні.

, де

–Ця величина становить статичний

момент

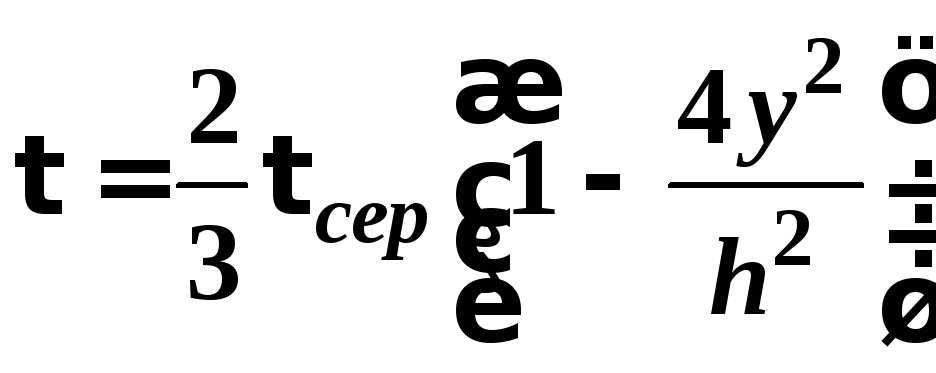Оскільки , то відповідно, щозвідки:

1. При 

2. При  .

2. Для круглого перерізу:

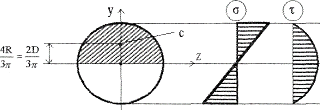
, де .

; –

такими будуть дотичні напруження при умові, що розподіляються вони рівномірно

3. Для двутаврового профілю:

Побудуємо епюри розподілу дотичних і нормальних напружень для двотаврової балки, і запишемо вирази для визначення дотичних напружень в точках 2' і 2', а також точки 3.

; ;,

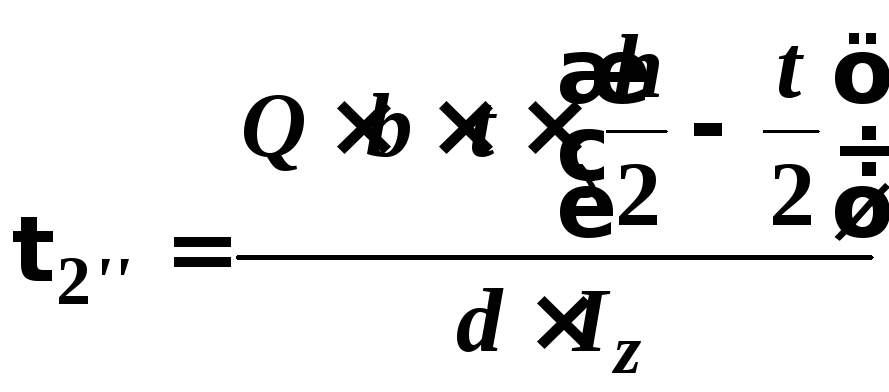де – теоретичний коефіцієнт концентрації напруження.

Перевірка міцності при плоскому згинанні брусу

При плоскому згинанні брусу проводять три перевірки його міцності:

1. Перевірка міцності по максимальних нормальних напруженнях (основна).

Перевіряються точки, що належать периферійним шарам тобто, таким які максимально віддалені від нейтрального шару.

Перевірка відбувається з урахуванням нормальних напружень по умові міцності при плоскому згині:

; .

2. Перевірка міцності по максимальних дотичних напруженнях.

Виконується для тих перерізів по довжині брусу в яких діють max по модулю поперечні сили. Тут буде чистий зсув і перевіряються, як правило, точки, що належать нейтральному шару. Перевірка проводиться по умові міцності для max дотичних напружень: , де

– для пластичних матеріалів;

– для крихких матеріалів.

3. Перевірка міцності по головних напруженнях.

Виконується для загрозливих перерізів (точок) по довжині балки.

Загрозливим наз. перерізи, в яких поперечна сила і згинальний момент не е екстремальними, але одночасно дуже близькі до них.

В загрозливих перерізах перевіряються точки по висоті перерізу.

Загрозливими є точки в яких і одночасно близькі по величині до своїхмах значень.

В двутаврі, наприклад, це точка - що належить перехідному шару, але відноситься до стінки.

В загрозливих точках перевірку міцності можна проводити двома шляхами:

1) по формулі – розрахувати головні напруження, враховуючи із якого матеріалу виготовлено балку, вибрати відповідну теорію міцності і підставити в неї замістьіїх значення, а. Порівняти аналітичне розраховані напруження з допустимими значеннямиіі зробити відповідні висновки.

2) Якщо в п'ять теорій міцності ми підставимо значення і(), то будемо мати:

І-а – – по першій теорій міцності;

ІІ-а – – по другій теорій міцності;

ІІІ-а – – по третій теорій міцності;

ІV-а – – по четвертій теорій міцності;

V-а – – по п’ятій теорій міцності,

де .

Всі ці теорії міцності називаються теоріями міцності, що застосовуються в випадку дії плоского згину.