Лекція № 7 Геометричні характеристики плоских перерізів

План лекції:

1. Статичний момент площі поперечного перерізу. Центр ваги. Приклади, визначення.

2. Моменти інерції площі поперечного перерізу. Основні особливості. Приклади визначення.

Література: [1] – 15÷21 с.

Статичні моменти площі перерізу. Центр ваги площі перерізу

Розглянемо довільний поперечний переріз стержня, що зв'язаний з координатними осями .

Виділимо елемент площі з координатами (), по аналогії з моментом сили відносно якої-небудь осі, і запишемо вираз для моменту площі перерізу, який і буде називатися статичним моментом площі перерізу.

(1) (1) – елементарні статичні моменти площі перерізу відносно осей і . Тоді повні статичні моменти всього перерізу будуть виглядати таким чином: ; . (см3) (2)

Для конструкційних елементів, площі перерізів і координати центрів ваги,яких відомі, статичні моменти площ розраховуються за формулами:

; . (3)

Приклад № 1.

1.Трикутник. Статичний момент площі перерізу трикутника є добуток його площі на відповідну координату центра ваги.

; .

2. Четверть круга

; ; .

Якщо необхідно знайти статичний момент площі круга відносно осів полярних координатах, то для цього необхідно виділити елементарний сектор з кутом. Довільним радіусом і проведемо дві дуги окружності.

Дано: ,,,, Визначити: Рішення: ; . Тоді:

.

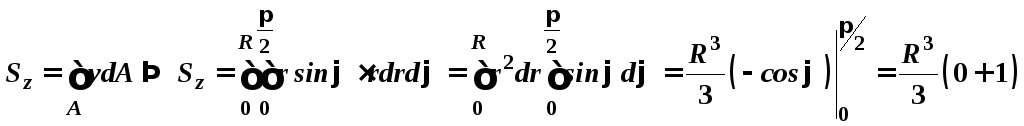
Аналогічно, відносно осідорівнює:.

3. Для складної фігури :

; ;

Статичним моментом площі перерізу відносно осі, що розглядається, називається величина, яка чисельно дорівнює інтегралу, вирахуваному по всій площі поперечного перерізу від добутку площі елементарної площадки на довжину (відстань) до осі, що розглядається.

Загальним методом визначення статичних моментів є метод інтегрування. Для простих перерізів, де відомо, як визначити їх площу і положення центру ваги, статистичний момент визначається як добуток площі перерізу, що розглядається на відстані від центру її ваги до довільної осі.

Статистичний момент площі перерізу може бути: додатнім, від'ємним і дорівнювати нулеві.

Осі, відносно яких статистичні моменти площі перерізу дорівнюють нулю, називаються центральними.

Моменти інерції плоских фігур

Осьовим моментом інерції площі перерізу відносно осі, що розглядається, називається інтеграл, який розраховується по всій площі поперечного перерізу від добутку площі елементарної площадки на квадрат відстані, до осі, що розглядається.

; (см⁴)

Осьові моменти ізавжди більші нуля.

Приклад:

; . Аналогічно:

Визначити .

Для визначення моменту інерції відносно осівибираємо елементарну полосну довжиноюі висотою. Тоді площа цієї елементарної смужки буде дорівнювати:.

Із подібності двох трикутників можемо записати:

.

Проводячи вісь через основу трикутника ми не накладали на його форму ніяких умов. Таким чином, момент інерції любого трикутника відносно осі, що приходить через його основу буде дорівнювати .