Метрологія / КонЛекМетр / TEMA_8

ТЕМА 8: ВИПАДКОВІ ПОХИБКИ

Навіть при ідеальному виключенні систематичних похибок не можна визначити справжнє значення величини, яка вимірюється, з-за неминучої появи малих відхилень окремих результатів вимірювання, які змінюються за знаком та абсолютним значенням випадково. Ці малі відхилення, які викликані дією численних іх факторів, у метрології називають випадковими похибками.

Абсолютнi значення i знак випадкових похибок пiдпорядковуються вiрогiдносним законам. З теорії ймовірності відомі наступні стандартні апроксимації законів розподілення густин вірогідностей:

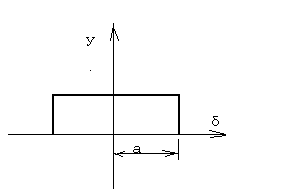1. Рiвномiрне розподiлення - характеризується графіком:

тут  – величина випадкової похибки;

 — середньоквадратичне відхилення ряду спостережень;

Y – густина вiрогiдностi або частота, з якою зустрiчаеться величина похибки.

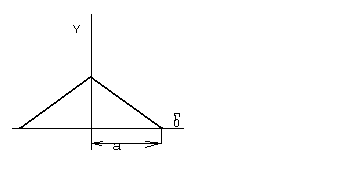
2.Трикутне розподiлення (розподілення Сiмпсона):

3. Нормальне розподiлення (розподілення Гауса).

Базуеться на двох аксіомах Гауса:

1) При дуже великiй кiлькостi вимiрювань, випадкові похибки, рiвнi по величенi та протилежнi по знаку, зустрiчаються однаково часто.

2) Частiше усього зустрiчаються малi похибки, а великі зустрічаються тим рідше, чим вони більше.

Нормальний закон розподілення описується виразом:

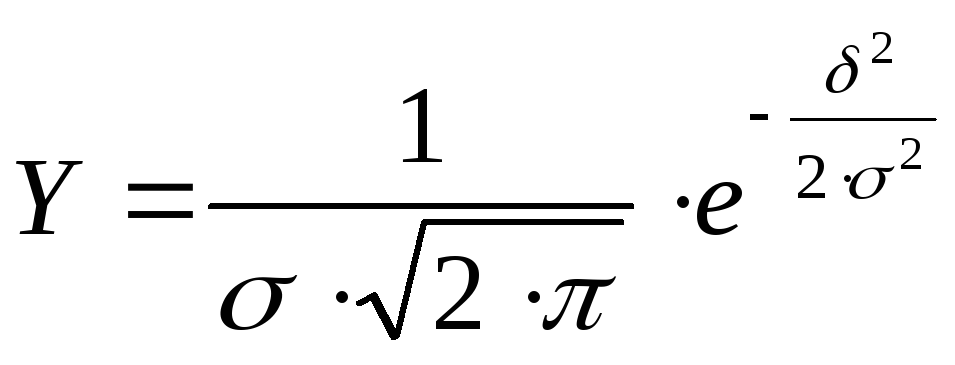
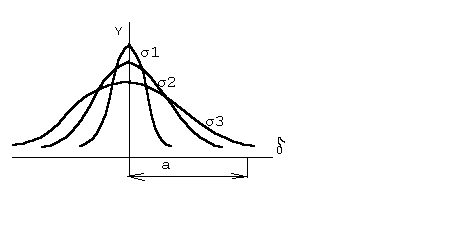
Характеризується графіком:

Випадкова похибка  являє собою рiзницю мiж результатом одиночного вимірювання i математичним очiкуванням результату:

Величина М[X] математичного очикування ряду спостережень наближуеться до його середнього значення.

Випадкова похибка також характеризуеться дiсперсiею або розсiюванням результатiв довкола середнього значення:

Іншою характеристикою розсіювання є середньоквадратичне вiдхилення (СКВ):

Точкова та інтервальна оцінки результатів вимірювань

Оцiнку результата вимiрювання виконують за методом точкових та iнтервальних оцiнок.

Нехай маемо ряд результатiв вимірювань: X1, X2, ... , Xi. Параметрами, що оцінюються, є математичне очiкування результатiв та дисперсiя.

Оцiнка результату (точкова а* ) зветься точковою, якщо вона виявляеться одним числом. Така оцiнка сама є випадковою величиною зі своїм розподiленням і підпорядковується вiрогiдносним законам.

Точковi оцінки математичного очiкування та дисперсii знаходять за формулами:

,

тут N – кількість вимірів (знак * позначає точкову оцінку).

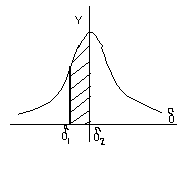
Iснує також iнтервальна оцiнка результатiв вимiрювання. Сутнiсть методу iнтервальної оцiнки полягає в знаходженнi iнтервала ( який зветься довiрчим), у межах якого з визначеною вiрогiднiстю (яка також зветься довірчою) знаходиться справжне значення оцiнюваємого параметра.

Вiрогiднiсть ( Р ) появи похибки із значеннями від 1 до 2 визначаеться площею дiлянки, яка залежить від висоти інтервалу, тобто кількості появи похибок Y та ширини від ₁ до ₂

Для нормального закона розподiлення вiрогiднiсть появи похибки обчислюється як визначений інтервал від функції Y :

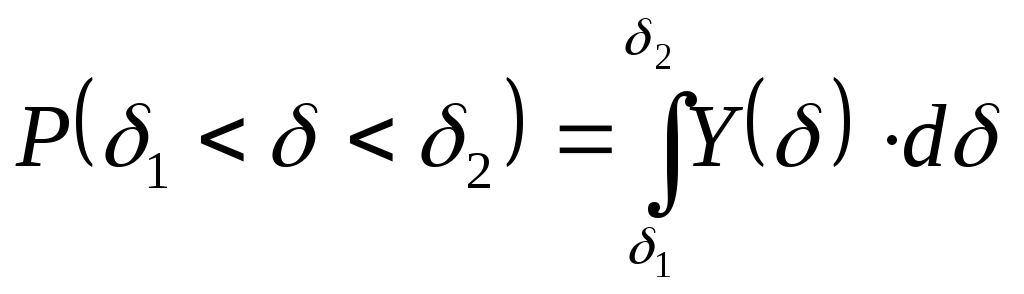
Значення цього iнтеграла для усiх величин  є стандартними i зведенi в спецiальнi таблицi.

На практицi ширину довiрчого iнтервалу  прийнято нормувати в значеннях :

,

де К = 1,2,3,... .

Так як на практиці похибки величиною > 3  малоймовірні, звичайно приймають щирину довiрчого iнтервалу .

При цьому Р = 0.997 , тобто тільки у трьох випадках із 1000 вимiрювань значення похибки вийдуть за межі довірчого інтервалу.

Ця формула справедлива, якщо кiлькiсть вимiрювань бiльше тридцяти. Якщо n < 30 , тодля оцінювання результатів вимірювання користуються розподiленням Стьюдента :

,

n – кiлькiсть вимiрювань;

p – потрiбна вiрогiднiсть.

Значення коефiцiента Стьюдента t_nр – розрахованi експериментально i зведени в спеціальні таблицi.

Порядок обробки результатiв при прямих вимiрюваннях

Нехай маємо ряд результатів вимірювання X1, X2, ... , Xn. Існує стандартна методика обробки багатократних спостережень. Для отримання результату необхідно виконати ряд операцій:

1. Записати результати вимiрювань з урахуванням поправок на систематичнi похибки, визначеним по формулах або таблицях поправок.

2. Визначити середнє арифметичне результатiв вимiрiв:

3. Визначити вiдхилення кожного вимiрювання вiд середнього, тобто величину випадкової похибки:

.

4. Визначити квадрати похибок .

5. Визначити суму квадратів похибок .

6. Визначити середньоквадратичне вiдхилення

7. Здiйснити по одному із стандартних методів (наприклад, методу Пірсона) перевiрку гiпотези про нормальнiсть закона розподiлення.

8. По заданiй довiрчiй вiрогiдностi та кiлькостi вимiрювань визначити коефiцiєнт Стьюдента t_nр, а також значення довiрчого iнтервалу :

9. Записати кiнцевий результат у виглядi :

Значення Хср та  округляють до двох знаків після коми. Результат записується у круглих скобках, після них проставляються одиниці вимірювання. Потім вказується величина довірчої ймовірності. Наприклад:

U_o = (15,37 ± 0,05)В, (Р =0,9).

Обробка даних при побiчних вимiрюваннях

При побiчних вимiрюваннях результат знаходять шляхом обчислення вiдомої аналiтичної залежностi мiж невiдомою величиною та величинами , якi одержані при прямих вимiрюваннях.

Припустимо, що результат побiчного вимiрювання представлений формулою :

,

де А₁, ... , А_n – результати прямих вимiрювань;

К₁, ... ,К_n – показники ступеня, в яких вони входять у формулу. Показники можуть бути додатнiми, вiд'ємними, цiлими та дробовими.

Прологарiфмуємо рiвняння:

.

Продиференціюємо:

Замiнимо диференціал малим приростом :

Величина , тобто дорівнює величині відносної похибки :

Вiдноснi похибки можуть бути бiльшими та меншими вiд нуля, тому для знаходження вiдносноi максимальноi похибки A складові беремо по модулю:

Якщо результати побiчних вимiрювань знаходяться в залежностi вигляду:

,

можна за аналогічною методою дiстати вираз вигляду для випадкових похибок вигляду:

.

Приклад розрахунку:

Вимiрюється потужнiсть розсiювання на резiсторi R. Відносна похибка вимірювання опору резистора , похибка вимірювання падiння напруги на ньому . Визначити можливу вiдносну похибку вимiрювання потужностi _p .

Звідси маємо величину похибки:

Загальний порядок додавання похибок

В цей час у відповідності до ДСТ 8.009-84 “Нормуємі метрологічні характеристики засобів вимірювань” усі похибки додаються наступним чином: окремо додаються систематичні та випадкові похибки і окремо мультиплікативні і адитативні похибки.

Таким чином, порядок додавання похибок наступний:

а) відбувається підготовка до додавання, при цьому похибки поділяються на систематичні та випадкові складові, адитивні та мультиплікативні; для випадкової складової похибки знаходять математичне очикування, СКВ та закон розподілення; визначають кореляційні зв’язки між складовими похибки;

б) відбувається додавання систематичних похибок усього приладу вцілому;

в) відбувається додавання випадкових складових похибки усього приладу вцілому, при цьому додають усі математичні очикування випадкових похибок і отриманий додаток математичного очикування додають до систематичної похибки (розглядаючи останню як випадкову похибку) і таким чином отримують систематичну складову сумарної похибки засобу вимірювання; знаходять значення СКВ випадкової складової похибки та закон розподілення сумарної випадкової похибки;

г) визначаються межі, в яких з довірчою вірогідністю

з находяться значення помилки  даного конкретного засобу вимірювання на базі наступної нерівності:

при заданих , , де k – коефіціент, який визначається довірчою вірогідністю та виглядом додаткового закону розподілення.