
- •Учебное пособие
- •Содержание
- •1. Физические основы механики
- •1.1. Основные формулы
- •1.2. Примеры решения задач к разделу «Механика»
- •1.3. Базовые задачи для самостоятельного решения
- •1.4. Контрольные вопросы
- •2. Основы молекулярной физики и термодинамики
- •2.1. Основные формулы
- •2.2. Примеры решения задач к разделу «Молекулярная физика и термодинамика»
- •2.3. Базовые задачи для самостоятельного решения
- •2.4. Контрольные вопросы
- •Библиографический список
- •Приложения
- •1. Основные физические постоянные (округленные значения)
- •2. Некоторые астрономические величины
1.2. Примеры решения задач к разделу «Механика»
Пример
№
1.
Движение тела массой 2 кг задано
уравнением:
![]() ,
где путь выражен в метрах, время – в
секундах. Найти зависимость ускорения
от времени. Вычислить равнодействующую
силу, действующую на тело в конце второй
секунды, и среднюю силу за этот промежуток
времени.
,
где путь выражен в метрах, время – в
секундах. Найти зависимость ускорения
от времени. Вычислить равнодействующую
силу, действующую на тело в конце второй
секунды, и среднюю силу за этот промежуток
времени.
|
Дано:
|
Решение: Закон изменения мгновенной скорости находим, продифференцировав уравнение движения:
|
|
|
Мгновенное ускорение определяется как производная от модуля скорости по времени:
![]() (2)
(2)
Среднее ускорение определяется выражением:
![]() (3)
(3)
где
υ2
– мгновенная скорость в момент времени
t2,
а
![]() 1
– в момент времени t1.
Из уравнения (1) находим:
1
– в момент времени t1.
Из уравнения (1) находим:
![]() ;
;![]()
После подстановки:
![]() (4)
(4)
Равнодействующая сила, действующая на тело, определяется по второму закону Ньютона:
![]() или
или
![]()
Подставив в эти формулы значения мгновенного и среднего ускорения (формулы (2) и (4)), получим формулы для вычисления искомых значений сил:
![]() ,
,
![]() (Н)
(Н)
![]() ;
;
![]() (H).
(H).
Ответ:
![]() ,
,![]() ,
,![]() .
.
Пример № 2. По наклонной плоскости, составляющей с горизонтом угол 30º, движется тело массой 5 кг. К этому телу с помощью нерастяжимой нити, перекинутой через блок, привязано тело такой же массы, движущееся вертикально вниз (рис. 1). Коэффициент скольжения между телом и наклонной плоскостью 0,05. Определить ускорение тел и силу натяжения нити.
|
Дано:
|
|
|
|
Решение: Покажем на рисунке силы, действующие на каждое тело. Запишем для каждого из тел уравнение движения (второй закон Ньютона):

В проекциях на выбранные оси координат:
![]() на
ось (z)
на
ось (z)
![]() на
ось (x)
на
ось (x)
![]() на
ось (y)
на
ось (y)
Учитывая,
что
![]() ,
где
,
где![]() ,
получим систему уравнений:
,
получим систему уравнений:

Вычтем из первого уравнения второе:
![]()
Отсюда искомое ускорение равно:
![]()
Подставим числовые данные и вычислим значение ускорения а:
![]()
Силу натяжения найдем из уравнения (1) системы:
![]() ;
;
![]()
Ответ: ![]() ,
,![]() .
.
Пример № 3. Найти линейные ускорения движения центров тяжести шара и диска, скатывающихся без скольжения с наклонной плоскости. Угол наклона плоскости равен 30º. Начальная скорость тел равна нулю.
-
Дано:


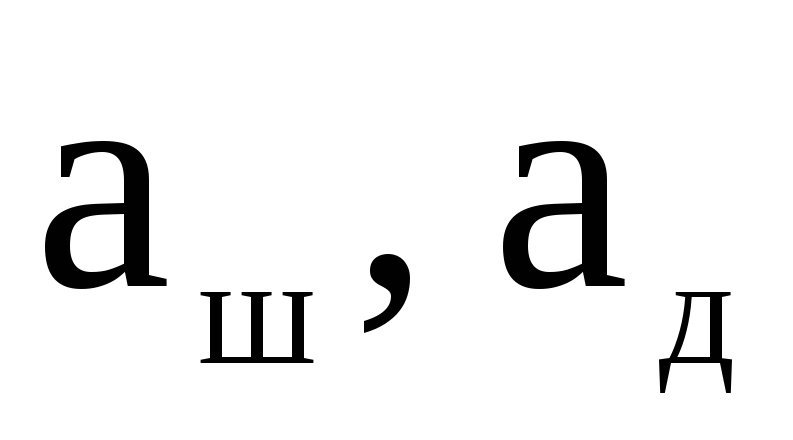 -
?
-
?
Решение: При скатывании тела с наклонной плоскости высотой h его потенциальная энергия переходит в кинетическую поступательного и вращательного движения. По закону сохранения энергии:
![]() (1)
(1)
где I - момент инерции относительно центра масс тела, m – масса тела; , ω – соответственно линейная и угловая скорости тел.
Длина наклонной плоскости l связана с высотой соотношением (рис. 1):
![]() (2)
(2)
Линейная скорость связана с угловой:
![]() (3)
(3)
После подстановки формул (2) и (3) в формулу (1), получим:
![]() (4)
(4)
Так
как движение происходит под действием
постоянной силы (силы тяжести), то
движение тел – равноускоренное. Начальная
скорость
![]() ,
по условию, поэтому:
,
по условию, поэтому:
![]() (5) и
(5) и ![]() (6)
(6)
Подставляя формулы (5), (6) в формулу (4), получим:
 (7)
(7)
Моменты инерции тел относительно оси, проходящей через центр масс соответственно равны:
|
для шара: |
|
|
для диска: |
|
Подставляя выражение для момента инерции в формулу (7), получим:
|
для шара: |
|
|
|
|
|
для диска: |
|
Ответ: ![]() ,
,![]() .
.
Пример № 4. Материальная точка массой 10 г совершает гармоническое колебание с периодом Т=1 с. Определить амплитуду колебаний, максимальную скорость и ускорение колеблющейся точки, если полная энергия точки равна 0,02 Дж.
|
Дано: m = 10 г = 10-2кг T = 1 с W = 0,02 Дж |
Решение:
Уравнение гармонического колебания
запишем в виде:
|
|
A,
|
Скорость колеблющейся точки среды определяется как первая производная от смещения по времени:
![]()
Максимальное
значение скорости:
![]() .
Ускорение точки определяется как
производная от скорости по времени:
.
Ускорение точки определяется как
производная от скорости по времени:![]() .
.
Максимальное
значение ускорения:
![]() .
.
Полная энергия складывается из кинетической и потенциальной энергии и равна максимальной потенциальной или максимальной кинетической энергии:
![]()
Круговая частота
связана с периодом
![]() :
. Тогда:
:
. Тогда:![]()
Из этого выражения
найдем амплитуду:
![]() .
.
Проверим размерность:
![]() .
.
Произведем вычисления:
![]() ,
,
![]() (с-1),
(с-1),
![]() ,
,
![]()
Ответ:
![]() ,
,![]() ,
,![]() .
.
Пример № 5. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных гармонических колебаний, данных уравнениями: x1 = 0,02cos (5πt + π/2) м и x2 = 0,03cos (5πt + π/4) м. Построить векторную диаграмму сложения амплитуд.
|
Дано: x1 = 0,02cos (5πt + π/2) м x2 = 0,03cos (5πt + π/4) м
|
Решение: Построить векторную диаграмму – это значит представить колебание в виде вектора, длина которого равна амплитуде колебаний, а его угол наклона к оси абсцисс равен начальной фазе колебаний. |
|
А, α - ? Дать векторную диаграмму. |
П ри
вращении вектора с угловой скоростьюω
проекция его конца на ось будет совершать
гармонические колебания.
ри
вращении вектора с угловой скоростьюω
проекция его конца на ось будет совершать
гармонические колебания.
Из условия задачи А1=0,02 м = 2 см, α1= π/2, А2=0,03 м = 3 см, α2 = π/4.
Векторная диаграмма изображена на рисунке.
Результирующую амплитуду найдем по теореме косинусов:
![]()
Начальная фаза результирующего колебания находится по формуле:
![]()
Вычисления:
![]()
 ;
;
![]()
Ответ: А = 4,6 м; α=62о 46′.
Пример № 6. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания δ = 1,6; начальная фаза равна нулю. Смещение точки в начальный момент времени равно 4,5 см. Написать уравнение колебаний и найти смещение точки в момент времени спустя период Т.
|
Дано:
|
Решение:
Уравнение затухающих колебаний имеет
вид:
Подставим
ω, β, α в (1) и найдем уравнение затухающих
колебаний:
|
|
|
Для начального момента времени при t = 0:
![]()
Уравнение
колебаний имеет вид:
![]()
Смещение
в момент:
![]()
![]()
Ответ:
![]()
![]()




 ;
;

