
- •Міністерство освіти і науки україни
- •Індивідуальне завдання № 2. Теореми додавання і множення ймовірностей
- •Індивідуальне завдання № 3. Формула повної ймовірності. Формула бейєса
- •Індивідуальне завдання № 4, 5. Послідовність незалежних випробувань
- •Індивідуальне завдання № 6. Дискретна випадкова величина
- •Розрахунково-графічна робота № 1. Індивідуальне завдання № 7-9. Неперервна випадкова величина
- •Індивідуальне завдання № 10. Закони розподілу дискретної випадкової величини
- •Індивідуальне завдання № 11. Закони розподілу неперервної випадкової величини
- •Індивідуальне завдання № 12. Нормально розподілена випадкова величина
- •Індивідуальне завдання № 13. Двовимірна дискретна випадкова величина
- •Індивідуальне завдання № 14. Двовимірна
- •Індивідуальне завдання № 18. Статистичні гіпотези
- •Індивідуальне завдання № 19. Статистичні гіпотези
- •Індивідуальне завдання № 20. Критерій згоди
- •Індивідуальне завдання № 22. Випадкові процеси
- •Індивідуальне завдання № 23. Моделювання випадкових величин методом монте-карло
- •Індивідуальне завдання № 24. Системи масового обслуговування. Ланцюги маркова
- •Додаток 4
- •Додаток 5
- •Додаток 6
- •Додаток 7
Індивідуальне завдання № 14. Двовимірна
НЕПЕРЕРВНА ВИПАДКОВА ВЕЛИЧИНА
Задача.Двовимірна випадкова величина![]() має щільність розподілу
має щільність розподілу![]() в області
в області![]() ,
обмеженій лініями і
,
обмеженій лініями і![]() поза областю.
поза областю.
Знайти:1)
параметра; 2) функцію розподілу![]() ;
2)
;
2)![]() та
та![]() ;
3)
;
3)![]() та
та![]() ;
4)
;
4)![]() .
.
1.
![]() ,
,![]()
![]()
2.
![]() ,
,![]()
![]()
3.
![]() ,
,![]()
![]()
4.
![]() ,
,![]()
![]()
5.
![]() ,
,![]()
![]()
6.
![]() ,
,![]()
![]()
7.
![]() ,
,![]()
![]()
8.
![]() ,
,![]()
![]()
9.
![]() ,
,![]()
![]()
10.
![]() ,
,![]()
![]()
11.
![]() ,
,![]()
![]()
12.
![]() ,
,![]()
![]()
13.
![]() ,
,![]()
![]()
14.
![]() ,
,![]()
![]()
15.
![]() ,
,![]()
![]()
16.
![]() ,
,![]()
![]()
17.
![]() ,
,![]()
![]()
18.
![]() ,
,![]()
![]()
19.
![]() ,
,![]()
![]()
20.
![]() ,
,![]()
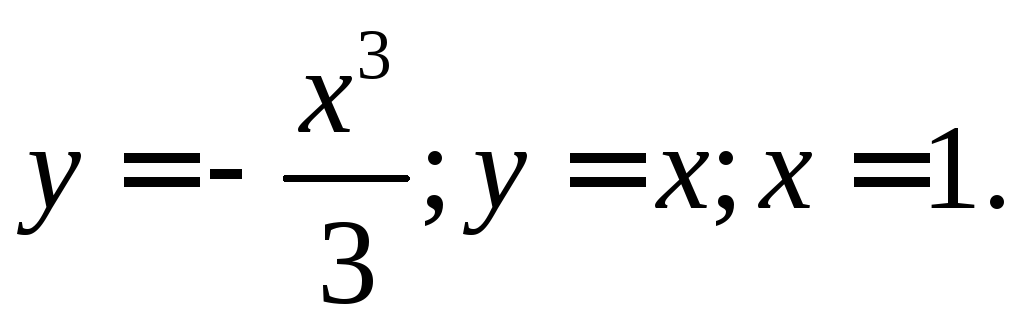
21.
![]() ,
,![]()
![]()
22.
![]() ,
,![]()
![]()
23.
![]() ,
,![]()
![]()
24.
![]() ,
,![]()
![]()
25.
![]() ,
,![]()
![]()
26.
![]() ,
,![]()
![]()
27.
![]() ,
,![]()
![]()
28.
![]() ,
,![]()
![]()
29.
![]() ,
,![]()
![]()
30.
![]() ,
,![]()
![]()
ІНДИВІДУАЛЬНЕ ЗАВДАННЯ № 15 (1-3), 16 (4-5).
СТАТИСТИЧНІ ОЦІНКИ ПАРАМЕТРІВ РОЗПОДІЛУ
При вивченні випадкової величини Ху результаті 25 незалежних спостережень дістали вибірку.
1. Побудувати
дискретний статистичний розподіл для
цієї вибірки, а також полігон частот,
![]() і кумуляту.
і кумуляту.
2. Обчислити
![]()
3. Знайти
![]()
![]()
4. Побудувати інтервальний статистичний розподіл для цієї вибірки, гістограму відносних частот.
5. Обчислити
![]()
![]()
![]() на основі інтервального статистичного
розподілу.
на основі інтервального статистичного
розподілу.
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() – де
– де![]() –
номер за списком.
–
номер за списком.
ІНДИВІДУАЛЬНЕ ЗАВДАННЯ № 17. ДОВІРЧІ ІНТЕРВАЛИ
На основі
інтервального статистичного розподілу
з індивідуального завдання № 16 знайти
довірчий інтервал для оцінки математичного
сподівання з заданою надійністю
![]() ,
вважаючи розподіл нормальним:
,
вважаючи розподіл нормальним:
а) при відомому
![]() ;
;
б) при невідомому
![]() .
.
|
№ за списком |
|
|
|
№ за списком |
|
|
|
1. |
0,6 |
0,93 |
|
16. |
1,1 |
0,85 |
|
2. |
1,7 |
0,93 |
|
17. |
2,2 |
0,84 |
|
3. |
0,3 |
0,92 |
|
18. |
0,5 |
0,92 |
|
4. |
1,4 |
0,95 |
|
19. |
1,3 |
0,93 |
|
5. |
1,2 |
0,84 |
|
20. |
2,2 |
0,84 |
|
6. |
1,3 |
0,83 |
|
21. |
0,2 |
0,93 |
|
7. |
2,4 |
0,95 |
|
22. |
0,9 |
0,84 |
|
8. |
1,1 |
0,84 |
|
23. |
0,4 |
0,93 |
|
9. |
1,3 |
0,93 |
|
24. |
2,3 |
0,83 |
|
10. |
0,4 |
0,82 |
|
25. |
1,4 |
0,91 |
|
11. |
2,5 |
0,83 |
|
26. |
1,5 |
0,84 |
|
12. |
1,4 |
0,94 |
|
27. |
1,2 |
0,95 |
|
13. |
2,5 |
0,93 |
|
28. |
2,2 |
0,92 |
|
14. |
1,3 |
0,92 |
|
29. |
2,3 |
0,91 |
|
15. |
1,3 |
0,92 |
|
30. |
2,1 |
0,92 |
Індивідуальне завдання № 18. Статистичні гіпотези
За статистичним
розподілом вибірки, що має нормальний
розподіл
![]() ,
одержаним в індивідуальному завданні
№ 16, при рівні значущості
,
одержаним в індивідуальному завданні
№ 16, при рівні значущості![]() перевірити правильність нульової
гіпотези
перевірити правильність нульової
гіпотези![]() (
(![]() – номер за списком) при альтернативній
гіпотезі:
– номер за списком) при альтернативній
гіпотезі:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
При перевірці кожної з альтернативних гіпотез розглянути два випадки:
а) при відомому
![]() (значення взяти в індивідуальному
завданні № 17);
(значення взяти в індивідуальному
завданні № 17);
б) при невідомому
![]() .
.
