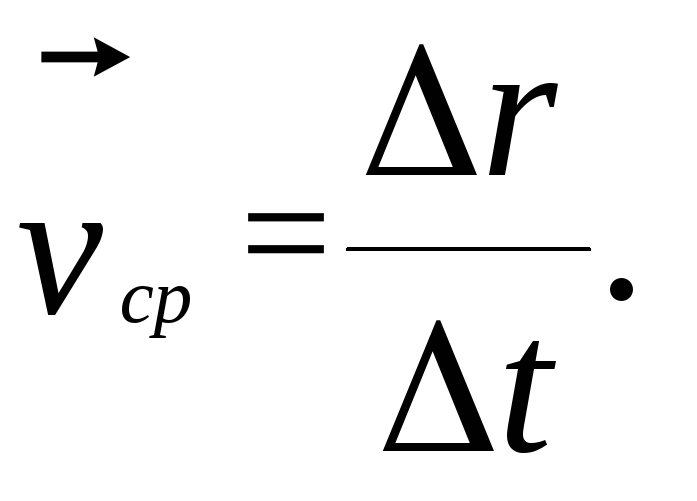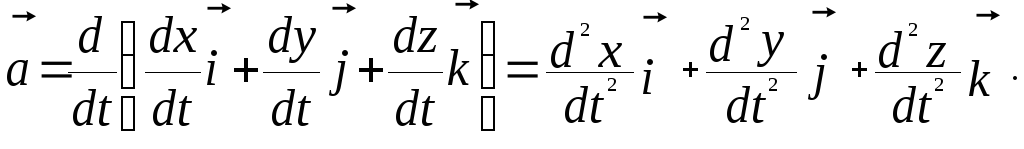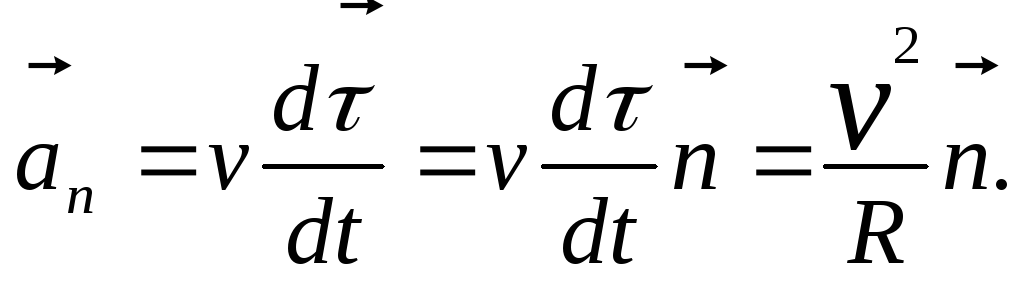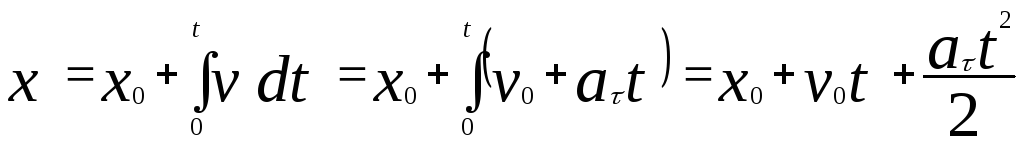Скорость

Полное описание движения материальной точки с помощью только вектора перемещения невозможно. Для характеристики движения материальной точки также вводят другую векторную физическую величину – скорость, определяющую как быстроту движения, так и направление движения в данный момент времени t.

Пусть материальная точка движется по криволинейной траектории MN (см. рис. 1.3) так, что в момент времени t она находится в точке M, а в момент времени t + t – в точке N. Радиус- вектора в точках M и N равны соответственно и , а длина дугиMN равна лине пути S.

Вектором средней скорости точки в интервале от t до t + t называется

(1.1.3)

Из формулы (1.1.3) видно, что вектор средней скорости сонаправлен с вектором перемещения Еслиt  0, то

- мгновенная скорость.

(1.1.4)

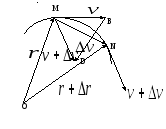
Рис. 1.3.

Схематическое изображение движения материальной точки

по криволинейной траектории

Вектор мгновенной скорости в точке M (см. рис. 1.3) направлен по касательной к данной точки траектории. Из математики известно, что при S  0 S/r = 1 и, как следствие, В этом случае можно ввести понятие путевой скорости: Из последнего выражения можно определить путь, пройденный точкой за данный промежуток времени:Необходимо отметить, что путевая скорость - скалярная величина.

Поскольку мгновенная скорость - векторная величина, то ее можно разложить на три составляющие по осям координат, то есть

(1.1.5)

Используя выражения (1.1.1) и (1.1.4), можно показать, что

(1.1.6)

Сравнивая выражения (1.1.5) и (1.1.6), можно определить проекции вектора скорости на декартовые оси координат: Последние позволяют рассчитать модуль скорости в данный момент времени: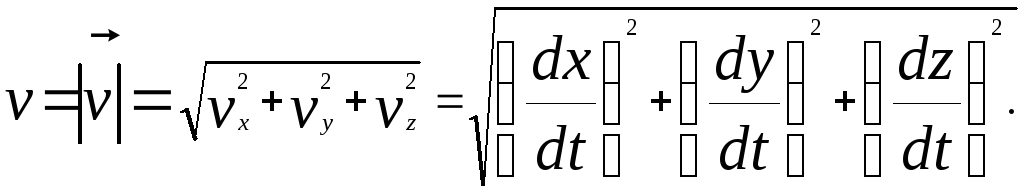

Рассмотрим некоторые частные случаи:

1. Скорость материальной точки не зависит от времени (равномерное движение). Поэтому для определения перемещения, пройденного точкой, можно использовать уравнение

(1.1.7,а)

а для определения пути

(1.1.7,б)

2. Скорость материальной точки является функцией времени (неравномерное движение). В этом случае

(1.1.8,а)

а для пути

(1.1.8,б)

где - средняя путевая скорость – это скорость, которая затрачивается для прохождения путиS за время t. В случае прямолинейного движения и, как следствие,. В общем случаеи.

В системе СИ единицей измерения скорости является Из закона независимости движений следует закон сложения скоростей:

Если материальная точка участвует в нескольких движениях, то результирующая скорость ее движения определяется как векторная сумма скоростей всех тех движений, в которых участвует материальная точка.

Ускорение

При неравномерном движении, кроме скорости, необходимо ввести другую характеристику – ускорение – меру быстроты изменения скорости. Пусть материальная точка за время t перешла из точки пространства M в точку N, а вектор скорости изменился на- вектор(см. рис. 1.3).Средним ускорением неравномерного движения в интервале t называется Вектор среднего ускорения сонапрален с вектором изменения скорости. Ускорением илимгновенным ускорением точки в момент времени t называется величина

(1.1.9)

Так как мгновенное ускорение – векторная величина, то

(1.1.10)

Из выражений (1.1.6) и (1.1.9) следует 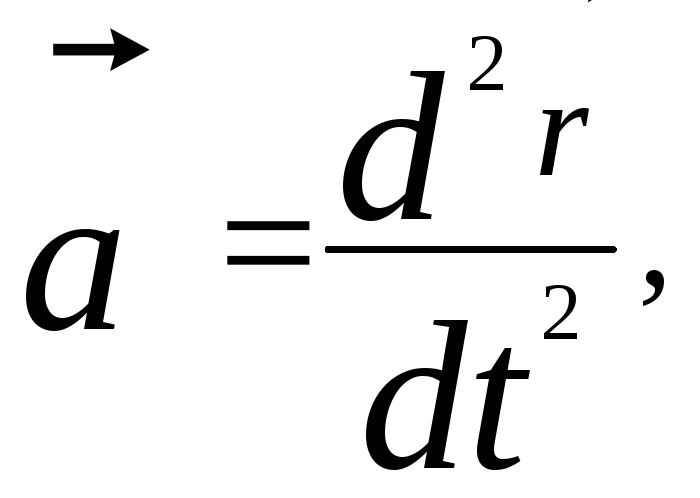и, как следствие:

(1.1.11)

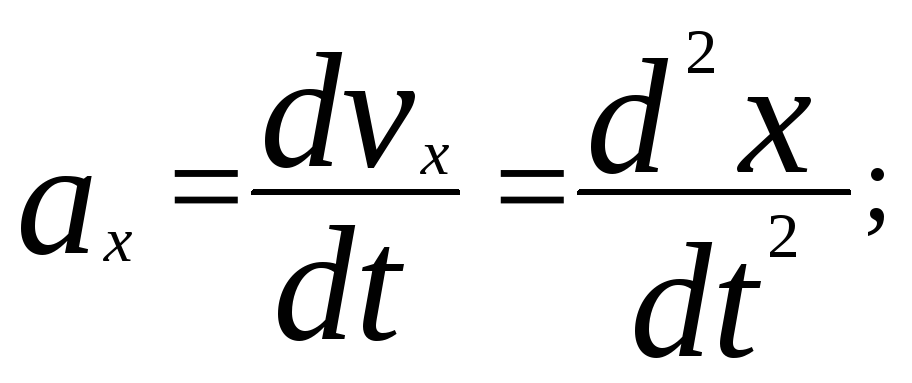
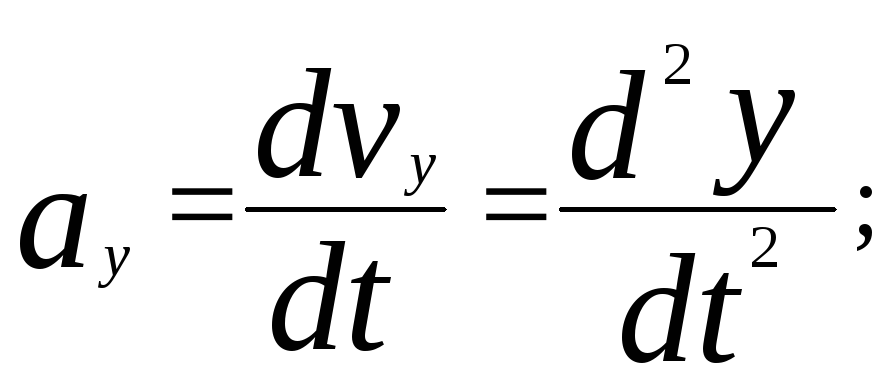
Таким образом, из (1.1.10) и (1.1.11) следует, что 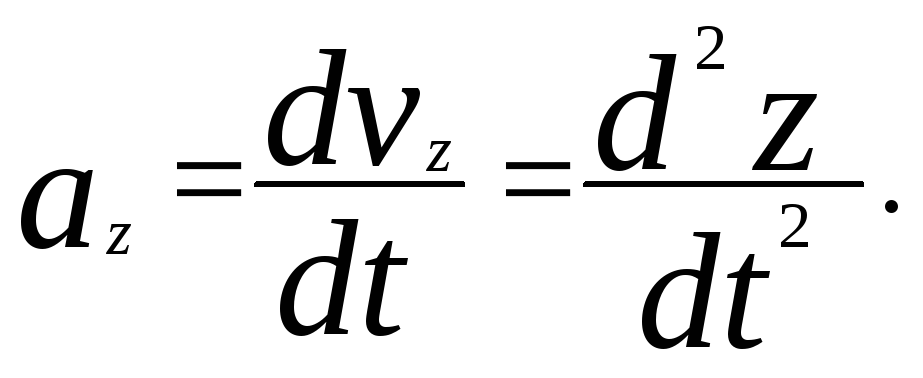Модуль вектора ускорения равен

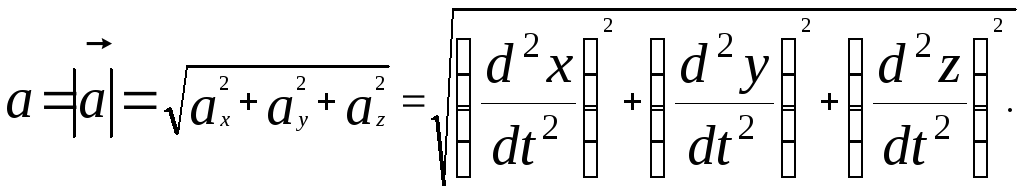
При рассмотрении плоского движения удобно пользоваться скользящей системой координат – системой, которая изменяет свое положение в пространстве вместе с движением материальной точки, то есть за начало отсчета принимают саму движущуюся точку. Одна ось вышеуказанной системы направлена по касательной к траектории движения материальной точки в данный момент времени (тангенциальная или касательная ось ), другая направлена перпендикулярно первой, и называется нормальной осью (см. рис. 1.4).

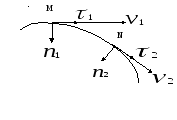
Рис. 1.4.

Схематическое изображение скользящей системы координат

Рассмотрим движение точки вдоль криволинейной траектории MN (см. рис.1.4). В скользящей системе координат скорость материальной точки можно представить как Из выражения (1.1.9) следует, что

Таким образом, ускорение материальной точки представляет собой сумму двух векторов, первый из которых показывает быстроту изменение модуля скорости материальной точки (тангенциальное ускорение), второй – быстроту изменения направления скорости (нормальное ускорение) (см. рис.1.4):

(1.1.12)

где

Покажем, что нормальное ускорение направлено по нормальной оси скользящей системы координат. Если и- единичные векторы осей скользящей системы координат, то скалярное произведение, а производная этой величины равна нулю. С другой стороны. Приравнивая полученное выражение к нулю, можно сделать вывод, что векторыиперпендикулярны друг другу (из определения скалярного произведения). Следовательно, нормальное ускорение перпендикулярно тангенциальной оси и направлено по нормальной оси скользящей системы координат.

Для определения физического смысла нормального ускорения рассмотрим равномерное движение материальной точки по окружности (см. рис. 1.5). В момент времени t₁ скорость точки – , в момент t₂ - . При равномерном движении модуль скорости остается постоянным (следовательно, тангенциальное ускорение равно нулю:), а направление вектора скорости меняется. Изменение единичного вектора равноЗа малый промежуток времениdt модуль вектора d можно определить как d = d, где d - угол поворота вектора скорости материальной точки. Поскольку  = 1, Из рис.1.5 видно, что dr = Rd (R – радиус окружности). Поэтому . Из приведенных выше выводов следует, что

(1.1.13)

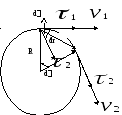
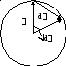
Рис. 1.5.

Схематическое изображение движения точки по окружности

При прямолинейном движении нормальная составляющая полного ускорения равна нулю (так как и). При равномерном движении по окружности, как отмечалось выше,. В общем случае при криволинейном движении имеют место и тангенциальная и нормальная составляющие полного ускорения, так что можно определить модуль полного ускорения: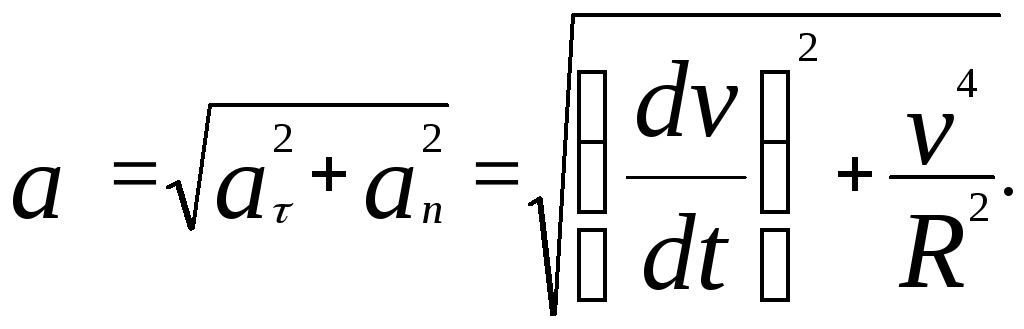Единицей измерения ускорения в системе СИ является

Простейшие виды движения материальной точки

1. Прямолинейное равномерное движение.

причем Поэтому

(1.1.14,а)

где x₀ – значение x в начальный момент времени (t = 0). Таким образом, для величины пути

(1.1.14,б)

2. Прямолинейное равнопеременное движение.

a_n = 0, a_ = const. При a_ > 0 – движение равноускоренное; При a_ < 0 – движение равнозамедленное; Из выражения (1.1.9) следует, что

(1.1.15)

где v₀ – начальная скорость. Для координаты

(1.1.16,а)

и пути

(1.1.16,б)

Часто для простоты записи в выражениях (1.1.15), (1.1.16,а) и (1.1.16,б) вместо a_ используют a.

3. Равномерное движение по окружности - наиболее простой вид криволинейного движения. Так как численное значение скорости в этом виде движения является постоянной величиной, , то величина скорости может быть определена черезс помощью выражения (1.1.13).