Лабораторна робота № 1. Графоаналітичний метод рішення задач лінійного програмування.

1.1. Загальна постановка задачі лінійного програмування.

Розв'язання систем лінійних нерівностей.

Означення. Нерівність називається лінійною, якщо вона містить змінні тільки у першому ступені, причому добуток змінних відсутній.

Загальний вигляд лінійної нерівності з двома змінними наступний . Ці нерівностіназиваються нестрогими. Нестрога нерівність еквівалентна рівнянню істрогій нерівності .

Множиною рішень рівняння є пряма, яка розбиває площину Х0У на дві півплощини.Множиною рішень нерівності є одна з цих півплощин. Щоб визначити, яка з них, потрібно вибрати контрольну точку (це може бути початок координат). Якщо координати контрольної точкиявляються рішенням нерівності, то координати всіх точок півплощини, на якій вибрана контрольна точка, теж є рішенням нерівності.

Означення. Множиною рішень лінійної нерівності є одна з півплощин, на яку пряма ділить площину Х0У, включаючи і цю пряму.

Приклад. Знайти множину розв’язків нерівності

Рішення:

Побудуємо пряму за точками перетину цієї прямої з осями координат: А(-2; 0) – точка перетину з віссю 0Х1. В(0; 3) – точка перетину х віссю 0Х2.

За контрольну точку візьмемо точку 0(0; 0) – початок координат. Після підстановки координат х1 = 0 і х2 = 0 в нерівність одержимо - нерівність не виконується. Отже розв’язком є верхня напівплощина разом з прямою (заштрихована частина).

Означення. Множиною розв’язків системи лінійних рівнянь нерівностей із двома невідомими є випуклий многокутник (крім випадку, коли система несумісна).

Приклад. Знайти множину розв’язків системи:.

Розвязок.

1) Побудуємо множину розв'язків першої нерівності (1).

2) Побудуємо множину розв'язків нерівності (2).

3) Побудуємо множину розв'язків нерівностей (3) і (4).

4) Побудуємо множину розв'язків нерівності (5).

5) Побудуємо множину розв'язків нерівності (6).

Таким чином, розв'язком системи лінійних нерівностей є випуклий многокутник. Координати вершин цього многокутника можна знайти, розв’язавши систему лінійних рівнянь прямих, на перетині яких знаходяться вершини.

Наприклад, щоб знати координати точки А, розв'яжемо систему двох рівнянь (4) і (6)  .

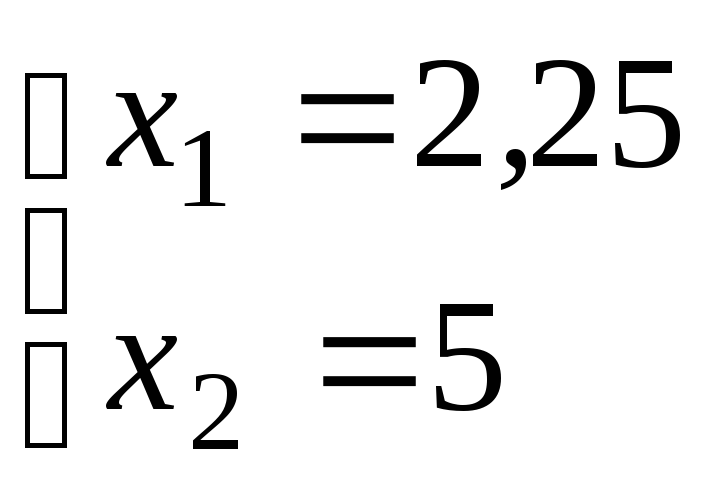Звідси, вершина А має координати А(2,25; 5).

Аналогічно можна визначити координати точки В(), як точки перетинання прямих (3) і (2), точки С(4; 0), як точки перетинання прямих (3) і (6) і т.д.

1.2. Графоаналітичний метод знаходження екстремуму лінійної функції двох змінних при заданій системі лінійних обмежень.

Задача лінійного програмування може бути геометрично інтерпретована у такий спосіб: накладені обмеження (4*) на змінні, які необхідно знайти хj геометрично зображуються деякою областю , яка утворює випуклий багатогранник в п - мірному просторі. Ця область називається областю припустимих планів, оскільки будь-яка точка в її межах відповідає вимогам (4*). З усіх припустимих планів нас цікавить оптимальний план, при якому цільова функція (3*) досягає оптимуму (максимуму чи мінімуму), тобто серед усіх точок багатокутної області  треба знайти ту, яка звертає у максимум цільову функцію (3*) . При цьому оптимальне рішення, якщо воно існує, обов’язково досягається в будь-якій вершині багатогранника. Щоб знайти розв’язок задачі лінійного програмування, досить розглянути лише ті плани, які відповідають вершинам багатогранника. Таки плани називаються опорними.

Розглянута геометрична інтерпретація задачі лінійного програмування можлива лише при наявності двох незалежних змінних. При трьох змінних наочне представлення значно ускладнюється, тому що в цьому випадку має місце деякий випуклий багатогранник у тривимірному просторі, що відповідає обсягу припустимих планів.

Цільовій функції Z відповідає сімейство паралельних прямих . Пам'ятаючи те, що напрям найшвидшого зростання функції Z вказує вектор, знайдемо координати цього вектора.

Означення. Пряма, яка може рухатися у напрямі найшвидшого зростання функції Z називається опорною прямою.

Якщо будемо рухати опорну пряму в напрямі вектора-градієнта, то перша спільна точка даної прямої і многокутника  буде точкою мінімуму цільової функції, а остання спільна точка – точкою максимуму.

Зауваження.Метод знаходження опорної прямої у випадку рішення задачі лінійного програмування може бути спрощеним. Так як цільова функція лінійна, тобто вона описується рівнянням прямої, то коефіцієнти при змінних в цьому рівнянні дорівнюють координатам вектора-градієнта.

Для розв'язку задач графоаналітичним методом по знаходженню екстремуму лінійної функції двох змінних з заданою системою лінійних обмежень необхідно:

 побудувати багатокутник допустимих розв’язків нерівностей системи;

 побудувати вектор-градієнт від початку координат і опорну пряму;

 рухати опорну пряму в напрямку градієнта, якщо необхідно знайти точку максимуму цільової функції; якщо треба знайти точку мінімуму, опорну пряму необхідно рухати протилежно напрямку градієнта;

 обчислити координати знайдених точок та значення цільової функції в цих точках.

Зауваження.При розв’язуванні задачі лінійного програмування графічним методом можуть бути такі варіанти розв’язків:

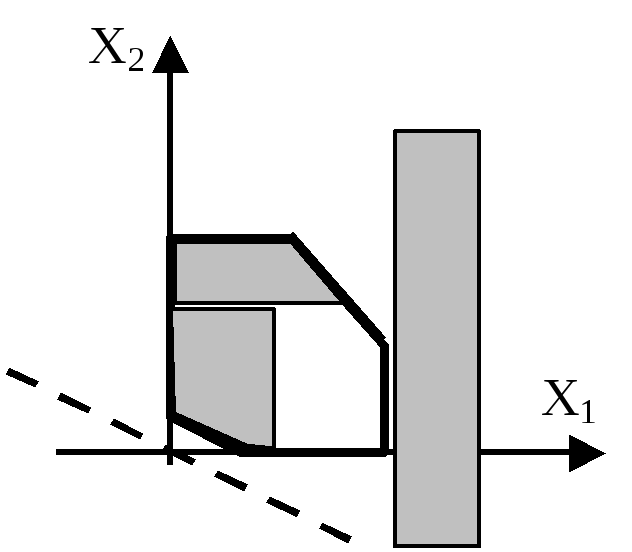
1. Задача не має розв’язку, оскільки система умов не сумісна, тобто не існує загальної області припустимих розв’язків – ОПР.

2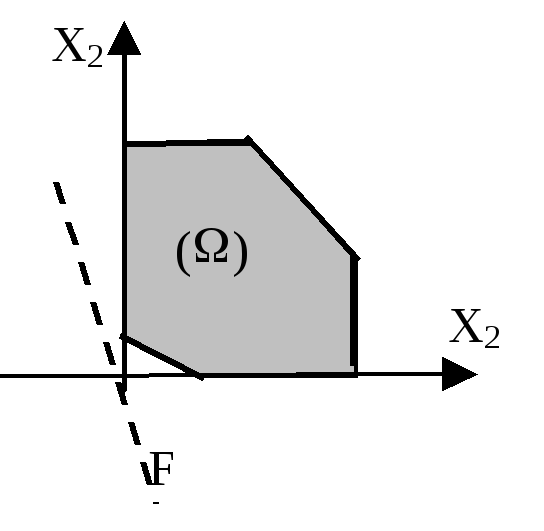. Задача має один єдиний розв’язок, система умов сумісна і цільова функція досягає свого екстремального значення в одній з вершин

багатокутника.

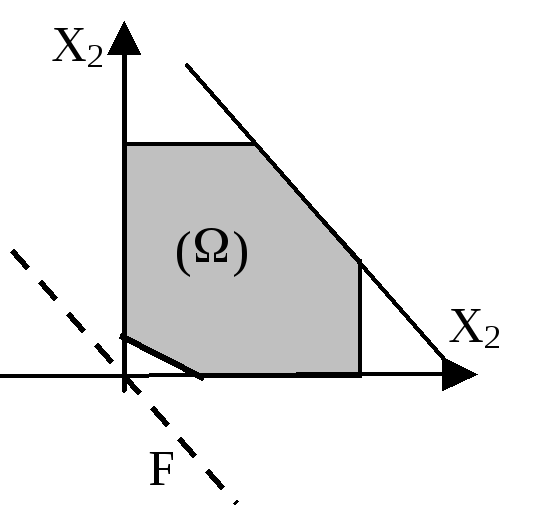
3. Задача має безліч розв’язків, тобто система умов сумісна, а цільова функція при прямуванні до екстремуму накладається на одну зі сторін багатокутника.

4. Задача не має розв’язку, оскільки ОПР не обмежена. Однак якщо ОПР не обмежена зверху, то цільова функція має тільки мінімум, якщо ОПР не обмежена знизу – цільова функція має тільки максимум.

Зауваження.При кількості змінних більш трьох задача втрачає геометричну наочність. Однак ідея одержання рішення зберігає зміст і для випадку багатомірного простору. Більш того, у багатьох випадках можна всі невідомі виразити через дві незалежні величини, вибрати ці величини як координатні вісі, представити обмеження і цільову функцію через них і вирішити задачу графоаналітичним методом.