Задание для самостоятельной работы
Задача 1. По следующим данным определите, в каком семестре уровень успеваемости студентов потока был выше:
|
Балл
|
Число студентов
|
|
|
1 семестр
|
2 семестр
|
|
|
"2" |
6 |
8 |
|
"3" |
32 |
20 |
|
"4" |
24 |
36 |
|
"5" |
18 |
16 |
Ответ: во 2 семестре средний балл составляет 3.75 против 3,68 в 1 семестре.
Задача 2. Имеются следующие данные о дневной реализации помидоров на рынках города:
|
Рынок
|
Объем реализации (руб.)
|
Средняя цена 1 кг (руб.)
|
|
1 |
4200 |
12 |
|
2 |
5880 |
14 |
|
3 |
10500 |
15 |
Вычислите среднюю цену 1 кг помидоров в целом по всем рынкам города.
Ответ: 14,0 рублей.
Задача 3.Известно распределение работников предприятия по возрасту:
|
Возраст, лет
|
Число работников, в % к итогу
|
|
до 25 |
14.0 |
|
25-35 |
22.0 |
|
35-45 |
20.0 |
|
45-55 |
17.0 |
|
55-65 |
15.0 |
|
65 и старше
|
12.0 |
Определите средний возраст работника. Ответ: 42 года.
Задача 4. По данным задачи 3 рассчитайте моду и медиану.
Ответ: Ми = 33 года, Ме = 42 года.
АНАЛИТИЧЕСКАЯ СТАТИСТИКА.
ПОКАЗАТЕЛИ ВАРИАЦИИ
Методические указания
Исследование вариации является составным элементом статистического анализа, позволяющим оценить колебания значений изучаемого признака, однородность совокупности по данному признаку, взаимосвязь его с другими признаками. Показатели вариации служат критерием типичности рассчитанных по совокупности средних величин, используются в определении ошибок выборочных характеристик.
При изучении данной
темы необходимо обратить особое внимание
на расчет основных показателей вариации
- дисперсии
,среднего
квадратического отклонения
среднего
линейного отклонения
,
коэффициента
вариации (
)
- по первичным и сгруппированным данным
(рядам распределения). Во втором случае
применяются не простые, а взвешенные
формулы соответствующих показателей.
Рассмотрим вычисление показателей вариации на следующем примере:
Таблица 8
Распределение предприятий торговли района по размеру торговой площади
|
Группы предприя-тий по размеру торговой площади, м2 |
Число
пред- прия-тий,
|
Середина
интервала ,
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
до 100
|
35
|
50
|
1750
|
185
|
6475
|
1197875
|
|
100-200
|
74
|
150
|
11100
|
85
|
629О
|
534650
|
|
200-300
|
119
|
250 |
29750
|
15
|
1785
|
26775
|
|
300-400
|
46
|
350
|
16100
|
115
|
5290
|
60850
|
|
400 и более брлееболее
|
27
|
450
|
12150
|
215
|
5805
|
1248075
|
|
ИТОГО
|
301
|
X
|
70850
|
615
|
25645
|
3615715
|
Заполнению последних
четырех граф данной таблицы предшествовал
расчет средней величины изучаемого
признака, выполненный по формуле средней
арифметической взвешенной:
Вычислим показатели
вариации:
Статистическую совокупность можно считать однородной по рассматриваемому признаку. если коэффициент вариации не превышает 33%. Таким образом, исследуемая совокупность является неоднородной, поэтому при рассмотрении исходных данных необходимо решить вопрос об исключении аномальных наблюдений (если такие имеются) или разбить совокупность на несколько групп, а затем определить показатели вариации у вновь образованных совокупностей.
При формулировке
выводов о степени вариации следует
обратить внимание на то, что коэффициент
вариации является относительной мерой
колеблемости и может приводить к
результатам, противоположным полученным
на основе абсолютных показателей
вариации. Так. например, если в первом
цехе дисперсия выработки деталей
работниками
=9
при средней выработке
-140,
а во втором цехе эти показатели
соответственно
=11
и
=170,
то абсолютная вариация будет сильнее
во втором цехе (
),
а относительная в первом
и
Наибольшую трудность
в изучении данной темы представляет
расчет
общей дисперсии по правилу сложения
дисперсий:
,
где
-
средняя из внутригрупповых дисперсий
,а
-межгрупповая
дисперсия,
,
где
и
- соответственно групповые средние и
численности по отдельным группам;
Правило сложения дисперсий может быть применимо только в том случае, когда совокупность разбита на две или более группы по какому-либо факторному признаку, предположительно оказывающему влияние на вариацию исследуемого признака.
Вариация признака
внутри групп определяется воздействием
всех
прочих факторов и отражается в величине
средней из внутригрупповых
дисперсий. Тесноту связи между факторным
и результативным признаками оценивают
с помощью эмпирического корреляционного
отношения
.
Данный показатель может принимать
значения от 0 до I
.
В статистическом
анализе широко используется показатель,
представляющий собой долю межгрупповой
дисперсии в общей дисперсии -эмпирический
коэффициент детерминации
,
он показывает долю (удельный вес) общей
вариации изучаемого признака,
обусловленного вариацией группировочного
признака.
На следующем условном примере исследуем зависимость между собственными и привлеченными средствами коммерческих банков региона:
Таблица 9
|
Банк
|
Собственные средства, млн. руб.
|
Привлеченные средства, млн. руб.
|
|
1 |
70 |
300 |
|
2 |
90 |
400 |
|
3 |
140 |
530 |
|
4 |
110 |
470 |
|
5 |
75 |
255 |
|
6 |
150 |
650 |
|
7 |
90 |
320 |
|
8 |
60 |
240 |
|
9 |
95 |
355 |
|
10 |
115 |
405 |
Произведем группировку банков, выделив две группы по величине собственных средств: до 100 млн. руб. и свыше 100 млн. руб., и проанализируем влияние данного группировочного признака (фактора) на размер привлеченных средств. Первая группа объединит коммерческие банки N-N 1, 2, 5, 7, 8, 9, во вторую группу войдут N-N 3, 4, 6. 10.
Расчет эмпирического корреляционного отношения состоит из
нескольких этапов:
1)
рассчитываем групповые средние и общую
среднюю по результативному
признаку - привлеченные средства (i
- номер группы,]
-
номер единицы в группе):
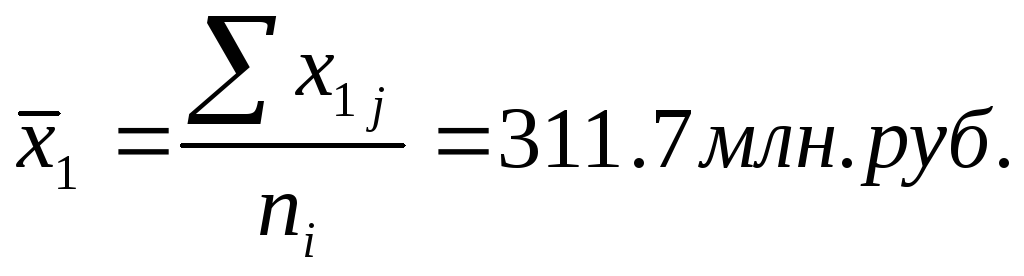
2) рассчитываем внутригрупповые дисперсии:
3) вычисляем среднюю из внутригрупповых дисперсий:
4)определяем межгрупповую дисперсию:
5) Находим общую дисперсию по правилу сложения
6)рассчитываем эмпирическое корреляционное отношение:
Полученная величина свидетельствует о том, что фактор, положенный в основание группировки (собственные средства), существенно влияет на размер привлеченных средств
Дисперсия альтернативного признака.
Альтернативные признаки – признаки, которыми обладают одни единицы совокупности и не обладают другие. ( Работники торговли подразделяются на мужчин и женщин, т.е. в данном случае это взаимоисключающие варианты.
Если возникает необходимость измерить вариацию альтернативного признака, то применяют следующее обозначение: 1- если интересующий нас признак в наличие ; 0 – если данный признак отсутствует.; долю единиц, обладающих данным признаком -p ; долю единиц не обладающим признаком -q .
Среднее значение
альтернативного признака
,
т.к. p+q=1
(сумма долей, обладающих и не обладающих
признакам равна единице)
Дисперсия альтернативного
признака:
,т.к.
,
т.к. p+q=1 подставим вместо 1-p
– q
Т.О. дисперсия альтернативного признака равна произведению доли единиц обладающих данным признаком и доли единиц им не обладающих.