Тестовые задания для самостоятельного решения
Легкое.Два равносильных шахматиста играют в шахматы. Вероятность выиграть одну партию из четырех равна ...
а) 1/2
б) 1/16
в) 1/4
г) 3/4
д) 1/8
Средней трудности.Игральная кость подбрасывается 5 раз. Вероятность того, что число очков, делящееся на три, выпало НЕ БОЛЕЕ четырех раз, равна…
а) 
б) 
в) 
г) 
д) 
Трудное.Игральная кость подбрасывается 5 раз. Вероятность того, что число четное очков выпало НЕ МЕНЕЕ четырех раз, равна…
а) 
б) 
в) 
г) 
д) 
Повышенной трудности.Игральная кость подбрасывается 5 раз. Вероятность того, что число очков, делящееся на три, выпало ровно три раза, равно…
а) 
б) 
в) 
г) 
д) 
Средней трудности. У Иванова в ящике для белья неупорядоченно лежит 10 пар носков: 5 пар черных, 3 пары белых и 2 пары синих. Иванов решил пойти на работу в черных носках и не глядя достает из ящика пару носков. Если ему не попалась пара носков черного цвета, он возвращает их в ящик и еще один раз повторяет попытку. Вероятность того, что Иванов пойдет на работу в черных носках равна ...
а) 1/4
б) 9/38
в) 29/38
г) 603/1444
д) 261/1444
Непрерывные случайные величины Основные определения
Функцией распределенияслучайной величиныξназывается функцияF(x), выражающая для каждогоxвероятность наступления события, заключающегося в том, чтоξпримет значение меньшее чемx.
.Случайная величина ξимеетабсолютно непрерывное распределение, если существует такая неотрицательная функцияfξ(x), что для любогоxфункция распределения представима в виде
.
При этом функцияfξ(x)
называетсяплотностью распределенияслучайной величиныξ.Математическое ожидание.
.
Основные свойства:
,
,
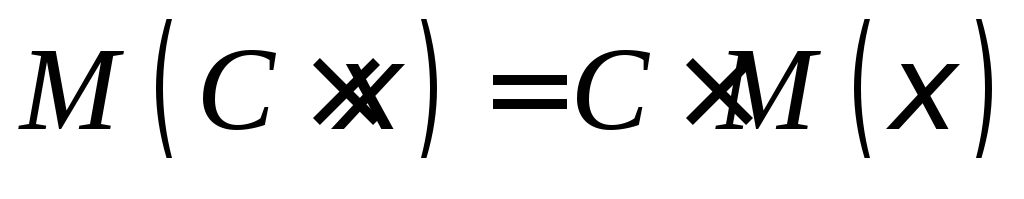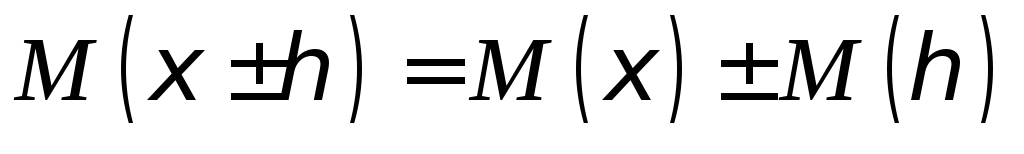.Дисперсия.
.
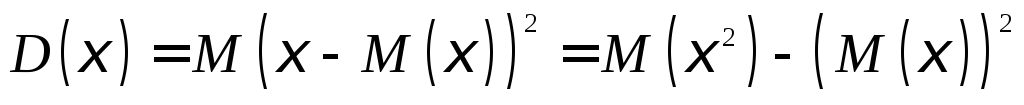Основные свойства:
,
,
.Равномерное распределение.
,
,
,
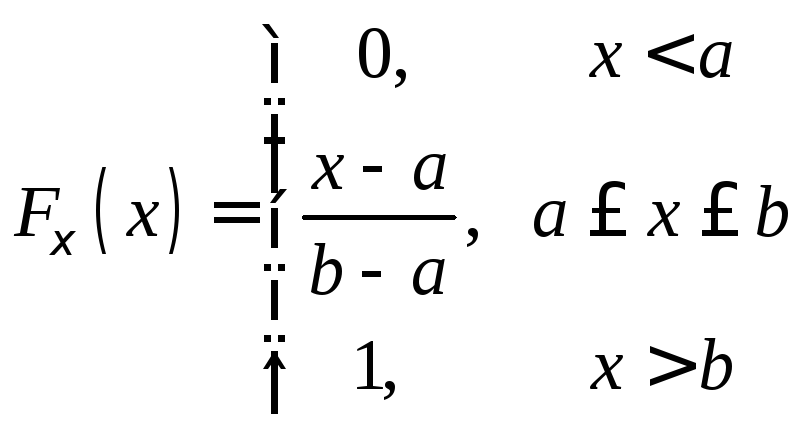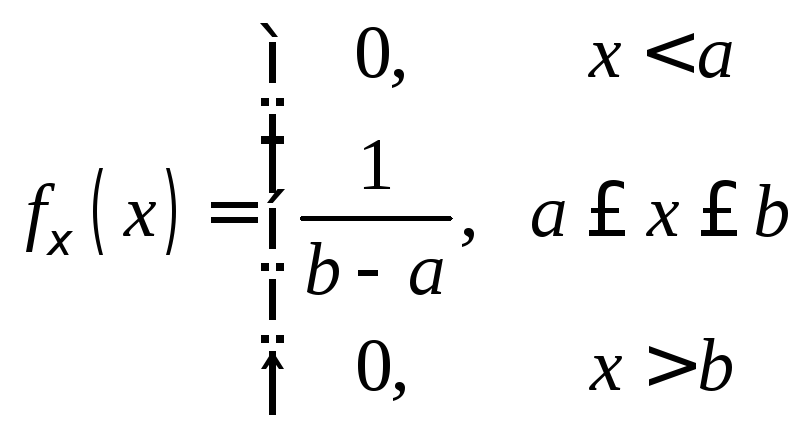.Нормальное распределение.
,
,
,
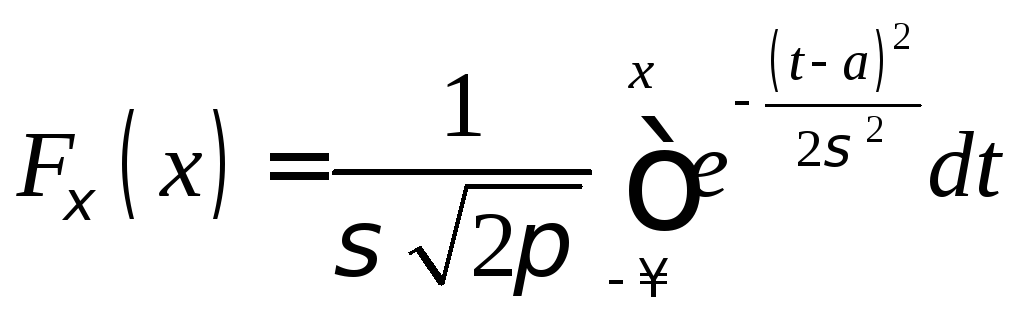.Стандартное нормальное распределение.
,
,
,
.
Примеры решения тестовых заданий
Если случайная величина Xзадана плотностью распределения
,
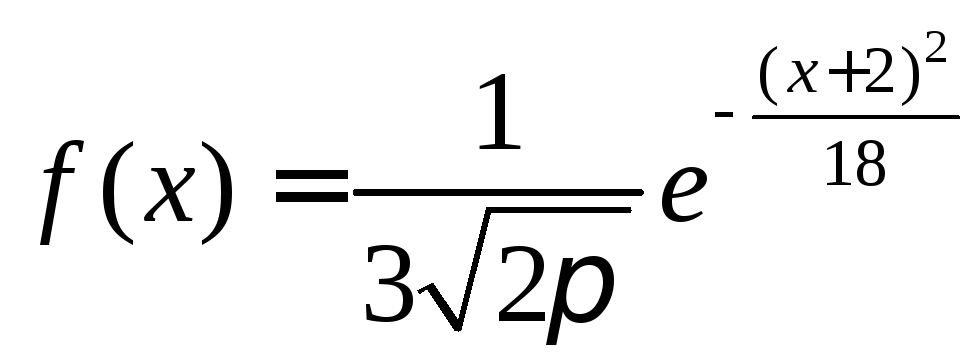то
…
Функция
задает плотность нормального распределения
(Определение 6.6.). Сопоставляя параметры,
мы приходим к выводу, что
.
Воспользуемся теперь свойствами
дисперсии (Определение 6.4.) и представим
в виде
.
Ответ:
.
График функции распределения случайной величины Химеет вид:
Тогда
…
На графике изображена функция равномерного распределения (Определение 6.5.) на отрезке [a,b]=[3,5]. По свойствам равномерного распределения
.
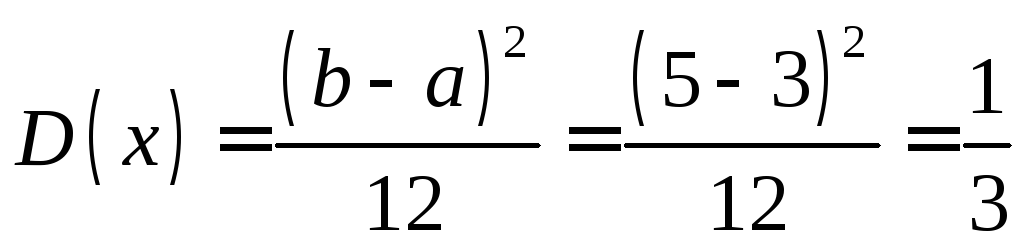Пусть Ф(x) это функция стандартного нормального распределения. Если Ф(x) = 0,65, то Ф(–x) равно ...
По определению
.
Докажем, что если
,
то и
.
.
Нужно запомнить, что нормально распределенная случайная величина, при смене ее знака с плюса на минус, не меняет своего распределения.
Пусть f(x) это функция стандартного нормального распределения. Еслиf(x) = 0,84, тоf(–x) равно ...
Функция плотности стандартного нормального распределения является четной, поэтому f(–x) = 0,84.
Тестовые задания для самостоятельного решения
Легкое.Если случайная величинаXзадана плотностью распределения
,
то
…
а) 5
б) 2
в) 0
г) 3
д) 1
Средней трудности.Случайная величинаXраспределена нормально с математическим ожиданиемa= 25. Вероятность попаданияXв интервал (10, 25) равна 0,2. Вероятность НЕ попаданияXв интервал (10, 40) равна ...
а) 0,4
б) 0,2
в) 0
г) 0,8
д) 0,6
Трудное.График плотности распределения случайной величиныХимеет вид:
Тогда
а) 1
б) 0
в) 0,5
г) -1
д) 5
Повышенной трудности.Если график функции распределения случайной величиныХимеет вид:
то
а) 0
б) 3
в) 1
г) 2
д) 4
Средней трудности.Пусть Ф(x) это функция стандартного нормального распределения. Если Ф(x) = 0,9, то Ф(–x) равно ...
а) 0,9
б) 0,05
в) -0,9
г) 0
д) 0,1