
- •3___Курс___________5-6___________семестр фно
- •Введение
- •Раздел I элементы линейной алгебры и аналитической геометрии
- •Раздел II математический анализ: функция одной переменной
- •Раздел III дифференциальное исчисление
- •Раздел V элементы многомерного математического анализа
- •Раздел VI интегральное исчисление
- •Раздел VII дифференциальные уравнения
- •Учебно-методические материалы
Раздел II математический анализ: функция одной переменной
Вопросы для подготовки к тестированию
Дайте определение функции. Что называется областью определения и областью значений функции?
Каковы основные способы задания функции? Приведите примеры.
Какая функция называется четной, нечетной? Приведите примеры.
Какая функция называется возрастающей (убывающей) на промежутке Р ?
Какая функция называется переодической? Приведите примеры.
Какие функции называются элементарными?
Перечислите основные элементарные функции.
Постройте график функции
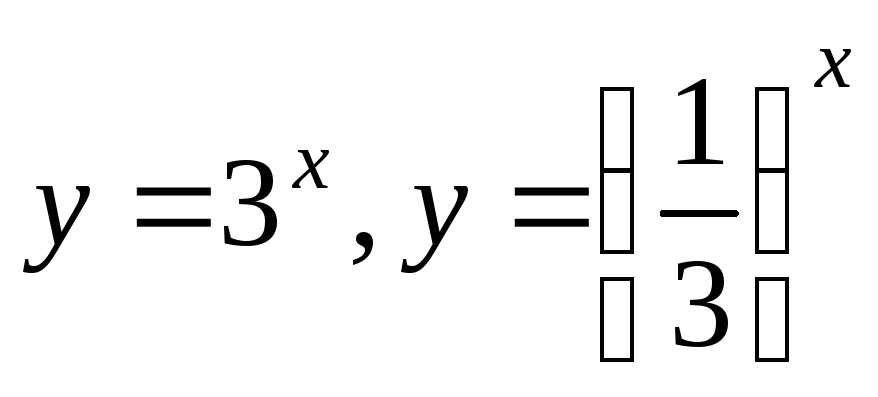 .
.Какая функция называется сложной?
Какая функция называется явной?
Какая функция называется неявной?
Какой вид имеет параметрическое задание функции?
Сформулируйте определение предела числовой последовательности.
Сформулируйте определение предела функции в точке и в бесконечности.
Какая величина называется бесконечно малой и каковы ее основные свойства ?
Какая величина называется бесконечно большой и какова ее связь с бесконечно малой ?
Сформулируйте основные теоремы о пределах функций.
Какой предел называется первым замечательным пределом?
Какой предел называется вторым замечательным пределом?
Сформулируйте основные правила раскрытия неопределенностей.
Сформулируйте определение непрерывности функции в точке.
Сформулируйте свойства функций непрерывных в точке и на отрезке.
Какие точки называются точками разрыва функции ?
Дайте определение точки разрыва первого рода.
Какую точку
 называют точкой устранимого разрыва?
называют точкой устранимого разрыва?Дайте определение точки разрыва второго рода.
Задачи для подготовки к тестированию:
Найти области определения следующих функций:
![]()
Ответ: а)![]() ;b)
;b)![]() ;c)
;c)![]() .
.
Определите, какие из данных функций являются четными, нечетными, общего вида.
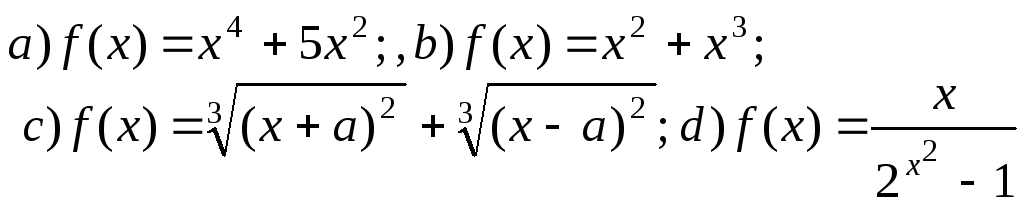 .
.
Ответ: a) четная;b) общего вида;c) четная;d) нечетная.
Найти пределы:
![]() ;
;
![]() ;
;
Ответ: 21; –2/3 .
Найти пределы:
а)![]() ;б)
;б)![]() ;в)
;в)![]() ;г)
;г)![]() ;
;
Ответ: а)![]() ;
б) 1;в)
;
б) 1;в)![]() ;г)
;г)![]()
Найти пределы:
а)![]() ;б)
;б)![]()
Ответ: а) 2;б) 0.
Найти пределы:
а)![]() ;б)
;б)![]()
Ответ: а) 6;б)
![]()
Исследовать на непрерывность функцию:

Ответ: в точке
![]() функция непрерывна, точка
функция непрерывна, точка![]() – точка разрыва первого рода.
– точка разрыва первого рода.
Раздел III дифференциальное исчисление
Вопросы для подготовки к тестированию:
Сформулируйте определение производной функции. Каков ее геометрический, экономический и механический смысл?
Запишите формулы производных суммы, произведения, частного двух функций. Приведите примеры.
Запишите формулу дифференцирования сложной функции.
Запишите формулы дифференцирования степенной, показательной, логарифмической и тригонометрических функций.
Как находится производная обратной и неявной функции?
Как находится производная функции, заданная параметрическими уравнениями?
Сформулируйте определение дифференциала функции.
Сформулируйте определения производной и дифференциала высших порядков.
Сформулируйте правило Лопиталя для раскрытия неопределенностей вида
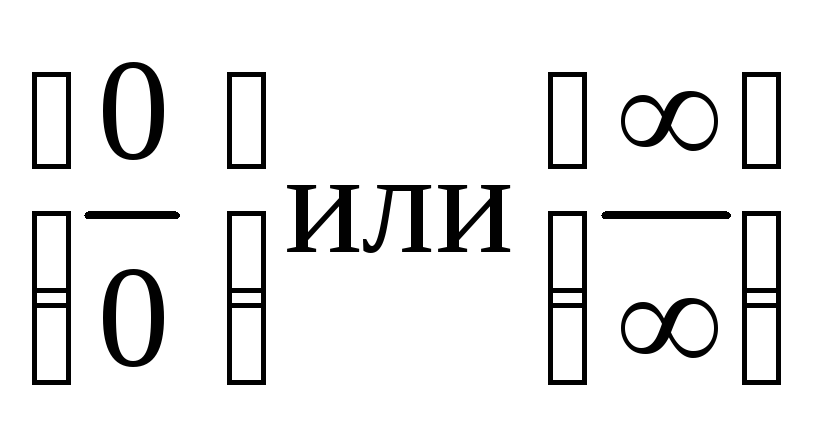 .
.Сформулируйте достаточное и необходимое условия возрастания и убывания функции.
Сформулируйте определение точки экстремума функции.
Дайте определение критической (стационарной) точки.
Сформулируйте первое и второе достаточные условия экстремума.
Как найти наибольшее и наименьшее значение функции на отрезке?
Сформулируйте условия выпуклости функции.
Что называется асимптотой графика функции?
Как определить вертикальные и наклонные асимптоты?
Изложите схему общего исследования функции и построения ее графика.
Задачи для подготовки к тестированию:
Вычислить производные следующих функций:
а)
![]() ;б)
;б)
![]()
Ответ: а)
![]() ;
б)
;
б)![]()
Вычислить производные сложных функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() ;
;
Ответ: а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() г)
г)![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
Составить уравнение касательной к кривой
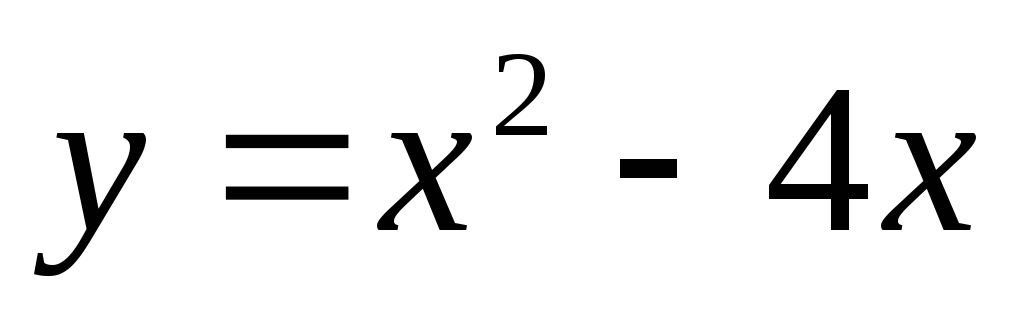 в точке с абсциссой
в точке с абсциссой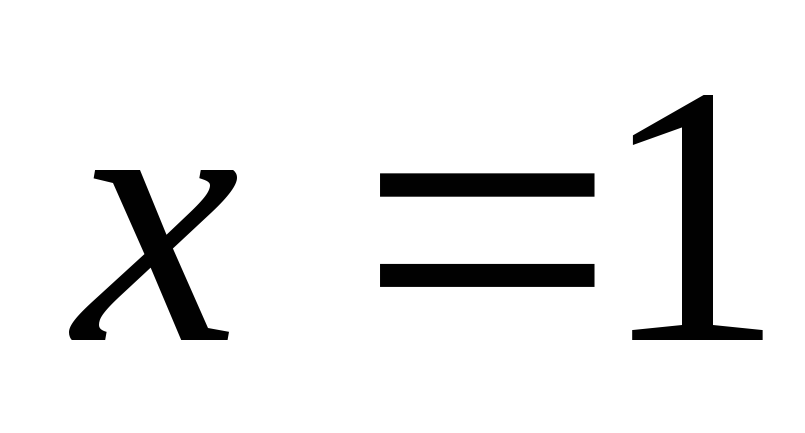 .
.
Ответ:
![]() .
.
Найти производную функции
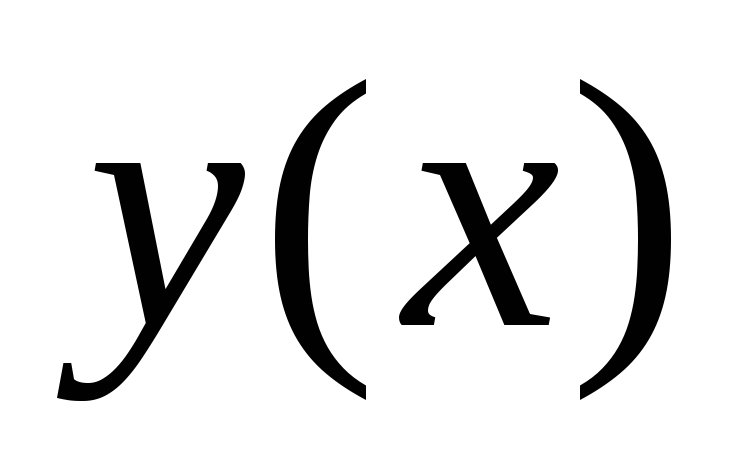 ,
заданной неявно
,
заданной неявно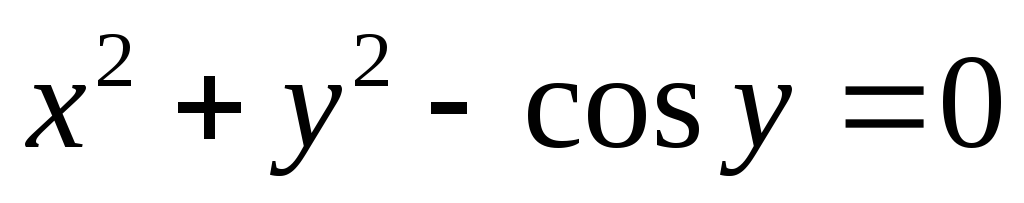 .
.Найти дифференциалы следующих функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
Ответ: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() .
.
Вычислить пределы, используя правило Лопиталя:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]()
Ответ: а) 2; б) 27; в) 1/9
Определить промежутки возрастания и убывания следующих функций:а)
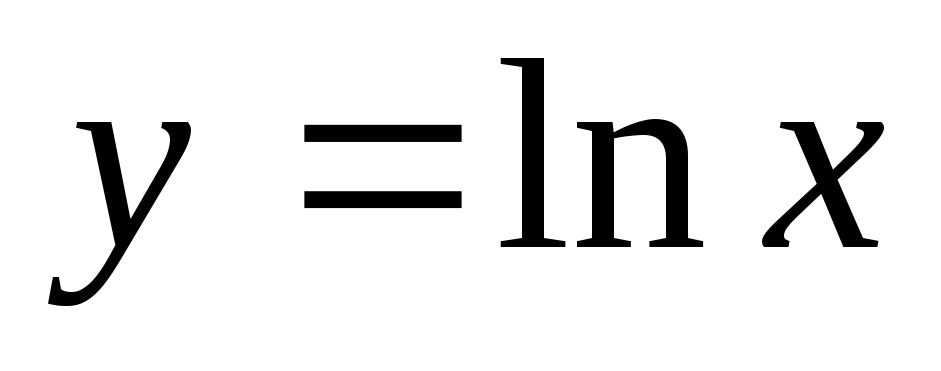 ;
б)
;
б)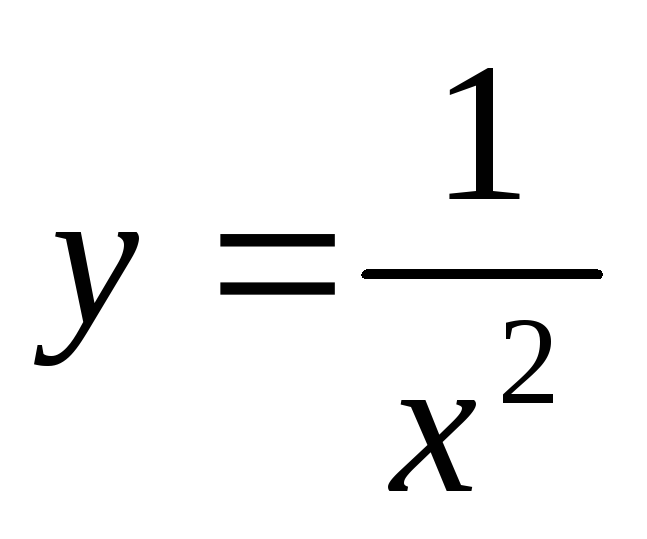 ;
в)
;
в)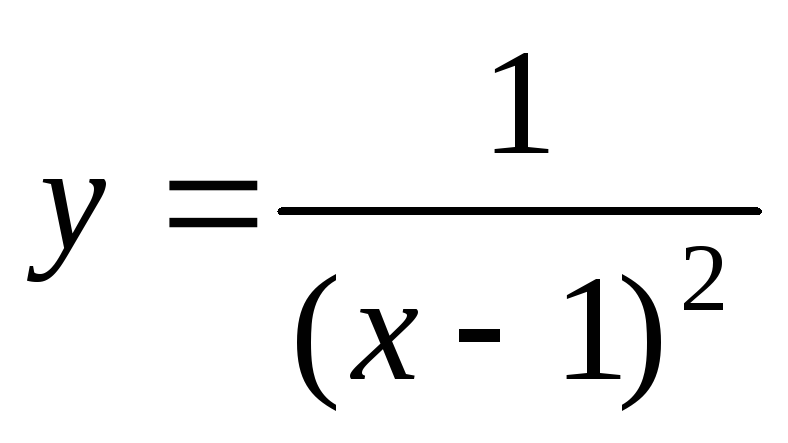 .
.
Ответ: а)
![]() – возрастает; б)
– возрастает; б)![]() – возрастает,
– возрастает,![]() – убывает; в)
– убывает; в)![]() – возрастает,
– возрастает,![]() – убывает
– убывает
Исследовать функции на экстремум:
а)
![]() ;
б)
;
б)![]() г)
г)![]() .
.
Ответ: а)
![]() – максимум ; б)
– максимум ; б)![]() – максимум,
– максимум,![]() – минимум; г)
– минимум; г)![]() – минимум,
– минимум,![]() – максимум.
– максимум.
Определить интервалы выпуклости и найти точки перегиба следующих функций:
а)
![]() ;
б)
;
б)![]() .
.
Ответ: а)
![]() – интервал выпуклости вверх,
– интервал выпуклости вверх,![]() – интервал выпуклости вниз; б)
– интервал выпуклости вниз; б)![]() – интервал выпуклости вверх,
– интервал выпуклости вверх,![]() – интервалы выпуклости вниз,
– интервалы выпуклости вниз,![]() – точки перегиба.
– точки перегиба.
Найти наибольшее и наименьшее значения каждой из следующих функций:
а)
![]() на отрезке
на отрезке![]() ;
б)
;
б)
![]() на отрезке
на отрезке![]() .
.
Ответ: а)
![]() – наибольшее значение,
– наибольшее значение,![]() – наименьшее значение; б)
– наименьшее значение; б)![]() – наибольшее значение,
– наибольшее значение,![]() – наименьшее значение.
– наименьшее значение.
