Метод указ к.р. Динамика

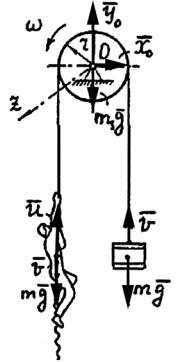
31

(рис.18)

Решение. (рис.18)

На систему тел действуют внешние силы: mg , m1g , а также

составляющие реакций опор оси ХО, YО.

На основании теоремы об изменении кинетического момента имеем dKdt z mz Fek ; mz Fek mgr mgr 0

K z const K z 0 ; K z 0 0; K z 0.(по условию задачи)

В данном случае выполняется закон сохранения кинетического момента системы относительно оси. Составим уравнение

mvr J z m(u v)r 0;

где Jz=1/2 (m1 r2) =0,1 (m r2).Здесь m1 =0,2m = v/r-угловая скорость блока .

m(u v)r 0.1mr 2 vr mvr 0.

Скорость груза

31

32

v 1021u .

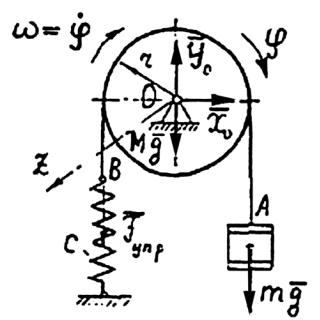
Задача 18 (рис.19)

Через блок массой M , имеющий горизонтальную ось вращения, переброшен трос, к одному концу которой подвешен груз массой m , а другой конец прикреплен к пружине жесткостью с. Пренебрегая трением и массой троса определить период малых колебаний системы, считая блок однородным цилиндром.

(рис.19)

Решение. (рис.19)

На рассматриваемую систему тел действуют внешние силы: Mg , mg ,

сила упругости пружины Fпр, а также составляющие реакций опор оси ХО,

YО.

Дифференциальное уравнение малых свободных колебаний диска получим с помощью теоремы об изменении кинетического момента:

dKdt z mz Fek .

mz Fek mgr F óïð f mgr c( f ct f )r c r2 ,

32

33

где F óïð c( f ct f ) -упругая сила пружины; f r - деформация

Кинетический момент системы относительно оси вращения барабана:

Kz J z mVr J ïðz . .

где J z 12 mr2 -момент инерции блока относительно оси вращения;

приведенный момент инерции системы.

Таким образом, проектируя уравнение на ось вращения блока, получим

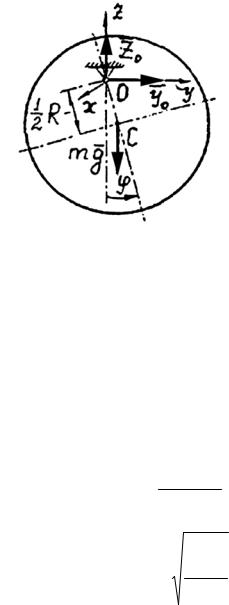
Задача 19 (рис.20)

Вертикально расположенный диск имеет горизонтальную ось вращения,

смещенную относительно центра масс диска на расстояние ОС R2 . В

начальный момент угол отклонения диска от равновесного положения равен

33

34

0 , а начальная скорость равна нулю. Считая колебания диска малыми определить закон движения диска.

Решение. (рис.20)

(рис.20)

Диск является физическим маятником. Дифференциальное уравнение вращательного движения диска имеет вид:

J mz Fek .

mz Fek mg R2 sin ,

где sin ; -угол поворота блока (малый угол).

mg R2 sin mgR2 .

mg R

k 2 0 где k 2 .

J z

Момент инерции диска относительно оси вращения:

Решение дифференциального уравнение вращательного движения диска ищется в виде:

34

Воспользуемся начальными условиями t 0 ; 0 и 0 . Найдем постоянные интегрирования

ОткудаC1 0 и C2 k0 0.

Уравнение движения диска

0 coskt .

ПРИНЦИП ДАЛАМБЕРА. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ.

Задача 20 (рис.21), (рис.22)

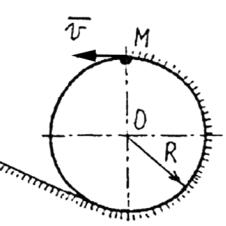
При каком минимальном значении скорости тяжелый шарик пройдет высшую точку петли радиуса R , не отрываясь от нее ? Петля расположена в вертикальной плоскости.

Решение. (рис.22)

35

36

(рис.22)

Будем считать шарик материальной точкой в промежуточном положении на его траектории. Приложим к шарику действующие силы: тяжести mg , нормальная реакция петли N и, соответственно, Ф , Фn- касательная и нормальная силы инерции.

Согласно принципу Даламбера для точки получим уравновешенную в любой момент времени систему сил

( m g , N , Ô ,Ô n ) 0 .

Проектируя эту систему сил на главную нормаль Mn, получим

R

Скорость шарика

V Rg .

36

37

Задача 21 (рис.23), (рис.24)

(рис.23)

Тяжелый шарик, находящийся на вершине гладкого сферического купола радиуса R , получает начальную горизонтальную скорость V0 . В каком месте шарик покинет купол? При каком значении начальной скорости V0 шарик оторвется от купола в верхней точке?

R

Согласно принципу Даламбера для точки получим уравновешенную в любой момент времени систему сил

( m g , N , Ô ,Ô n ) 0 .

Проектируя эту систему сил на главную нормаль Mn, получим mg cos N Ôn 0.

В момент отрыва шарика от купола нормальная реакция купола будет равна нулю:

37

38

(рис.24)

N mg cos mVR 2 0 .

Отсюда

V 2 Rg cos .

Воспользуемся теоремой об изменении кинетической энергии:

Искомое положение шарика, когда он покинет купол

cos 2 V0 2 . 3 3Rg

Отрыв шарика от купола произойдет при угле :

скорости:

V 2 Rg cos gR .

Итак, если V0 V gR , то шарик сойдет с купола в верхней точке.

38

39

Задача 22 (рис.25), (рис.26)

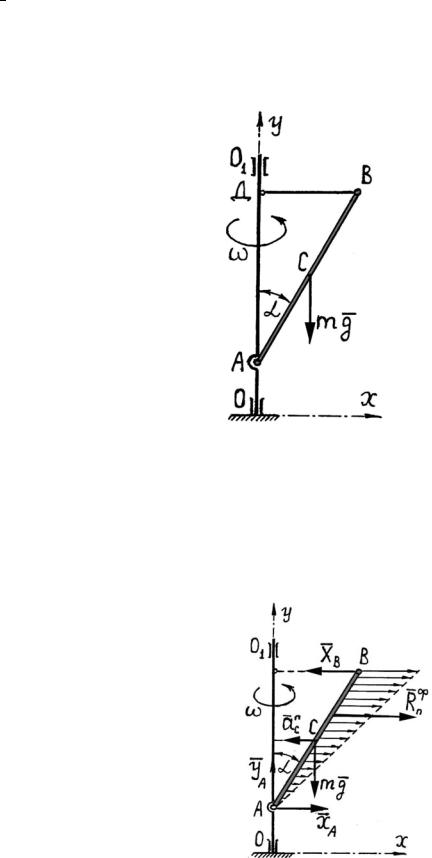
Однородный стержень АВ длиной l и массой m, закрепленный шарнирно на валу ОО1, вращается вокруг оси Оy с постоянной угловой скоростью ω. Стержень удерживается под углом α к вертикали при помощи горизонтальной тяги ВД . Найти реакции шарниров А и В.

(рис.25)

Решение. (рис.26)

Применим для решения задачи принцип Даламбера. Приложим к стержню силу тяжести mg , составляющие реакции ХА и УА шарнира А вдоль осей координат, реакцию ХВ шарнира В.

39

40

Силы инерции точек стержня заменим равнодействующей нормальной силой инерции RnФ , приложенной в точке К, причем RnФ macn m 2 2l sin ;

.

Получена уравновешенная в любой момент времени система сил

(mg, X A ,YA , X B , RnФ) ∞ 0,

acn 2 2l sin – нормальное ускорение центра масс стержня (точки С); АС =

СВ.

Условия мгновенного динамического равновесия стержня имеют вид:

X A X B RnФ 0; YA mg 0;

X Bl cos RnФ(23 l cos ) mg(12 l sin ).

Из составленной системы уравнений, с учетом значения силы RnФ , последовательно находим:

X B 12 mgtg 13 m 2l sin ; YA mg;

X A 12 mgtg 16 m 2l sin .

Задача 23 (рис.27), (рис.28)

Однородный гладкий диск массы m и радиуса r установлен между валом ОО1 и стержнем АВ, прикрепленным к нему под углом φ. Стержень и вал вращаются с постоянной угловой скоростью ω вокруг оси Оу (рис. 27). Определить давление диска на стержень и вал.

40