Фазовые превращения

Фазой называется термодинамически равновесное состояние вещества, отличаются не химическим составом, а физическим свойствами от других равновесных состояний того же вещества (например, вода может находиться в трех фазах: жидком, твердом и в виде пара). Переход вещества из одной фазы в другую называется фазовым переходом.

Различают фазовые переходы IиIIрода. Фазовый переходIрода связан с поглощением или выделением тепла (например, плавление и кристаллизация). Фазовый переходIIрода не связаны с теплотой (например, переход некоторых веществ при определенных температурах в сверхпроводящее состояние см. п.5.7).

Для характеристики фазовых переходов используются диаграммы состояний (обычно в координатах Р – Т). На этих диаграммах можно найти точку одновременного равновесного осуществления трех фаз – тройную точку. Например, тройная точка для воды 273,16 К. Термодинамика позволяет рассчитать равновесие двух фаз одного вещества, пользуясь уравнением Клапейрона – Клаузиуса:

,

где производная от равновесного давления по температуре зависит от теплоты фазового перехода λ, температуры перехода и изменения объема фаз (например, при замерзании воды ее объем возрастает).

Реальные газы. Уравнение Ван – дер – Ваальса

Уравнение Менделеева – Клапейрона для 1 моля идеального газа имеет вид: PV=RT. Молекулы реального газа имеют размеры ~10^-10м и поэтому следует учитывать их собственный объем, т.е. в уравнение Менделеева – Клапейрона вводится поправка «в» на объем, занимаемый самими молекулами (V₀– в).

Действие сил взаимодействия между молекулами реального газа приводит к дополнительному внутреннему давлению P_i=a/V₀², гдеV₀– объем 1 моля газа, т.е.

(Р + P_i) = (Р + a/V₀²)

Поправка «а» и «в» постоянны для данного газа. С учетом этого для 1 моля реального газа уравнение состояния – уравнение Ван – дер – Ваальса примет вид

(Р + a/V₀²) (V₀- в) =RT(6.54)

Это уравнение из-за сделанных упрощений также приближенно описывает состояние реального газа.

На рис. 6.10 проведены изотермы Ван – дер – Ваальса для различных температур. Если сравнивать их с изотермой идеального газа (рис.6.7), то заметим, что только при

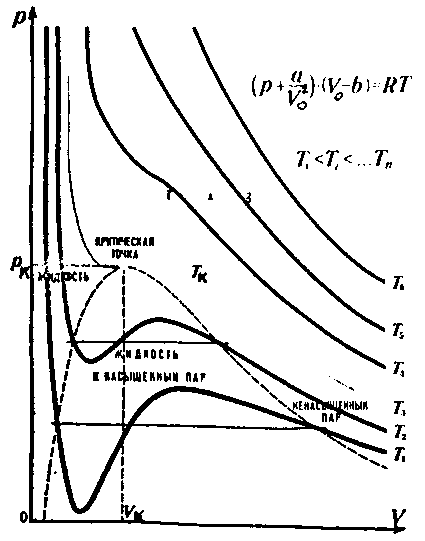
Рис.6.10

высоких температурах они схожи. При низких температурах изотермы отличаются горбами, при этом одному Р соответствует три объема. Среди изотерм Ван-дер-Ваальса есть такая, которая разграничивает изотермы с “горбами” от изотерм без “горбов”. Она отделяет области двухфазного состояния вещества (газообразного и жидкого) и однофазного (газообразного). Эта изотерма называется критической и соответствующие ей параметры Р,Vи Т также называются критическими. Понятие критической температуры Тк было введено Менделеевым. Менделеев рассматривал ее как температуру, при которой исчезают силы взаимодействия между молекулами и жидкость превращается в пар независимо от давления и занимаемого объема (на изотерме ей соответствуеткритическая точка).

6.3. Функции распределения. Закон Максвелла для распределения молекул по скоростям

Молекулы, находясь в состоянии непрерывного теплового движения, сталкиваются, обмениваются импульсами, поэтому скорости их неодинаковы (см.п.6.1). Максвелл для газа, находящегося в состоянии термодинамического равновесия, вывел закон распределения молекул идеального газа по скоростям. Обозначим число молекул,скоростикоторых заключены в интервале отVдоV+dV, черезdN.dNпропорциональноN-общему числу молекул и интервалуdV, т.е.

, (6.55)

где - функция распределения молекул, она определяет относительное число молекул из общего числа,скоростикоторых лежат в интервале отVдоV+dV. Эта функция, (6.56)

где константы ;;m- масса одной молекулы.

График f(V) представлен на рис.6.12

Рис.6.12

На графике выберем интервал скоростей молекул ΔV, тогда. На графике любому интервалу ΔVсоответствует площадь ΔS(заштрихована) под кривой, численно равная относительному числу молекул, скорости которых заключены в этом интервале ΔV. Из графика можно заключить, что относительное число молекул с малыми скоростями или с очень большими мало. Наибольшее число молекул имеют скорости, близкие кV_в–наиболее вероятной скорости.

(6.57)

С увеличением температуры Т максимум кривой на рис. 6.12 сдвигается вправо (в сторону больших скоростей), растет и величина V_в.

Наиболее удобно распределение Максвелла выражать через относительную скорость υ=V/V_в. Тогда

Экспериментальная проверка распределения Максвелла была выполнена Штерном.