
- •Мпс россии
- •1. Введение
- •2. Физические основы механики
- •Основные механические модели
- •1. Материальная точка.
- •2. Абсолютно твердое тело.
- •2.1. Кинематика материальной точки
- •Основные кинематические уравнения равнопеременного движения:
- •Движение материальной точки по окружности. Угловая скорость и угловое ускорение и их связь с линейными характеристиками движения
- •Для характеристики изменения вектора скорости на величину δv введем ускорение :
- •Угловая скорость и угловое ускорение
- •2.2. Динамика материальной точки и поступательного движения твердого тела
- •Взаимодействие тел. Второй закон Ньютона. Сила. Масса. Импульс. Центр масс
- •2.3. Законы сохранения в механике
- •Момент силы. Момент импульса. Закон сохранения момента импульса
- •Энергия. Работа. Мощность
- •Консервативные и неконсервативные силы
- •Закон сохранения энергии
- •2.4. Принцип относительности в механике
- •2.5. Элементы релятивистской динамики (специальной теории относительности)
- •2.6. Элементы механики твердого тела
- •2.7. Элементы механики сплошных сред
- •Упругое тело. Деформация. Закон Гука
- •3. Электричество и магнетизм
- •3.1. Электростатика
- •Закон Кулона
- •Электрическое поле
- •Принцип суперпозиции электрических полей
- •Поток вектора напряженности электрического поля
- •Теорема Остроградского – Гаусса и ее применение к расчету полей
- •Поле равномерного заряженной бесконечной прямолинейной нити
- •Поле равномерно заряженной плоскости
- •Работа сил электростатического поля при перемещении заряда. Потенциал
- •Связь между напряженностью и потенциалом электростатического поля
- •Идеальный проводник в электростатическом поле
- •Электроемкость уединенного проводника конденсатора
- •Энергия заряженного проводника
- •Энергия электрического поля. Объемная плотность энергии
- •3.2. Постоянный электрический ток
- •Закон Ома
- •Дифференциальная форма закона Ома
- •Закон Джоуля-Ленца
- •Закон Джоуля-Ленца в дифференциальной форме.
- •Правила Кирхгофа для разветвленных цепей.
- •3.3. Магнитное поле
- •Момент сил, действующих на виток с током в магнитном поле
- •Принцип суперпозиции магнитных полей
- •Закон Био-Савара-Лапласа и его применение к расчету магнитных полей
- •Взаимодействие параллельных токов
- •Контур с током в магнитном поле. Магнитный поток
- •Работа перемещения проводника и контура с током в магнитном поле
- •Явление электромагнитной индукции. Закон Фарадея
- •Явление самоиндукции
- •Токи замыкания и размыкания в цепи
- •Явление взаимоиндукции
- •Энергия магнитного поля
- •3.4. Статические поля в веществе Диэлектрики в электрическом поле
- •Магнитные свойства вещества
- •3.5. Уравнения Максвелла
- •Электромагнитные волны
- •3.6. Принцип относительности в электродинамике
- •3.7. Квазистационарное магнитное поле
- •4. Физика колебаний и волн
- •4.1. Кинематика гармонических колебаний
- •Сложение гармонических колебаний
- •4.2. Гармонический осциллятор
- •Свободные затихающие колебания
- •Логарифмический декремент затухания
- •4.3. Ангармонические колебания
- •4.4. Волновые процессы
- •4.5. Интерференция волн
- •Интерференция от двух когерентных источников
- •Стоячие волны
- •Интерференция в тонких пленках
- •4.6. Дифракция волн
- •Принцип Гюйгенса-Френеля
- •Дифракция Фраунгофера от одной щели
- •Дифракция от многих щелей. Дифракционная решетка.
- •4.7. Поляризация света
- •Поляризация при отражении света от диэлектрика
- •Двойное лучепреломление в анизотропных кристаллах
- •Закон Малюса
- •Степень поляризации
- •Вращение плоскости поляризации
- •4.8. Взаимодействие электромагнитных волн с веществом
- •5. Квантовая физика
- •5.1. Экспериментальное обоснование основных идей квантовой механики. Взаимодействие фотонов с электронами
- •Внешний фотоэффект
- •Эффект Комптона
- •Давление света
- •5.2. Корпускулярно – волновой дуализм
- •Соотношение неопределенностей
- •5.3. Квантовые состояния и уравнение Шредингера
- •5.4. Атом
- •Теория Бора для водородоподобных атомов.
- •5.5 Многоэлектронные атомы
- •5.6. Молекулы
- •5.7. Электроны в кристаллах
- •5.8. Элементы квантовой электроники
- •5.9. Атомное ядро
- •Радиоактивность. Закон радиоактивного распада
- •Закономерности α и β - распада
- •Ядерные реакции. Законы сохранения в ядерных реакциях
- •Реакция деления ядра. Цепная реакция. Ядерный реактор
- •Реакции синтеза. Термоядерные реакции
- •Элементарные частицы
- •6. Статистическая физика и термодинамика
- •6.1. Элементы молекулярно-кинетической теории
- •Модель идеального газа
- •Число степеней свободы молекул
- •Среднее число столкновений и средняя свободного пробега молекул
- •Явления переноса
- •Электрический ток в вакууме. Термоэлектронная эмиссия
- •Электрический ток в газах
- •6.2. Основы термодинамики Внутренняя энергия идеального газа. Работа
- •Внутренняя энергия идеального газа
- •Первый закон термодинамики
- •Изопроцессы
- •Термодинамические процессы, циклы
- •Круговые процессы. Второе начало термодинамики.
- •Цикл Карно
- •Фазовые превращения
- •Реальные газы. Уравнение Ван – дер – Ваальса
- •6.3. Функции распределения. Закон Максвелла для распределения молекул по скоростям
- •Барометрическая формула (распределение Больцмана)
- •Порядок и беспорядок в природе. Синергетика
- •Магнетики в тепловом равновесии. Ферромагнетизм
- •7. Заключение Современная физическая картина мира
Соотношение неопределенностей
Если электрон или другая микрочастица ведет себя аналогично волне, то возникает вопрос: можно ли точно указать координату частицы в пространстве (например, положение электрона на орбите в атоме). В 1927 году Гейзенберг пришел к выводу, что невозможно одновременно точно определить координату х частицы и ее импульса Р. Их можно определить лишь с погрешностью (неопределенностью) Δх и ΔР, причем соотношение между ними (при одномерном движении)
![]() ,
(5.19)
,
(5.19)
Формула (5.19) получила название соотношение неопределенностейГейзенберга. Оно имеет смысл для микромира: частицы в микромире ведут себя иначе, чем тела в микромире.
Например, для электрона со скоростью
![]() ,
найденной с погрешностью 10%, т.е.
,
найденной с погрешностью 10%, т.е.![]() получим неопределенность координаты
получим неопределенность координаты
![]()
что сравнимо с размерами атома. То есть, электрон в атоме находится, но где точно неизвестно.
Также существует соотношение неопределенностей для энергии и времени:
![]() ,
(5.20)
,
(5.20)
где ΔΕ-неопределенность энергии;
Δt-время жизни квантовой системы в данном энергетическом состоянии.
Соотношение (5.19) и (5.20) является проявлением дуализма свойств материи.
5.3. Квантовые состояния и уравнение Шредингера
Так как частицы
проявляют волновые свойства, хотя в
строгом понимании волной не являются,
то оказывается невозможным охарактеризовать
эти свойства с помощью уравнений
классической механики. Шредингер(1925г.), анализируя поведение частиц с
позиций квантовой механики, пришел к
выводу, что положение частицы в данный
момент времени можно определить с
помощьюволновой функции![]() .
Статистический смысл волновой Ψ - функции
состоит в том, что она определяет
вероятность ω того, что частица находится
в области Δх при одномерном ее движении
вдоль оси х. Вероятность ω пропорциональна:
.
Статистический смысл волновой Ψ - функции
состоит в том, что она определяет
вероятность ω того, что частица находится
в области Δх при одномерном ее движении
вдоль оси х. Вероятность ω пропорциональна:
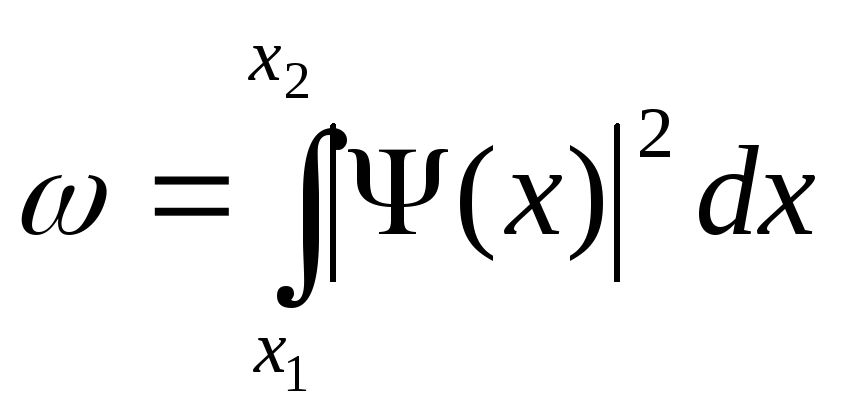 (5.21)
(5.21)
Такой подход хорошо согласуется с волновыми свойствами частиц и с соотношением неопределенностей (5.19). Основное (временное) уравнение Шредингера (при V<<с):
![]() ,
(5.22)
,
(5.22)
где m-масса
частицы;![]() ;
;![]() ;
;
Δ-оператор Лапласа;
U-потенциальная энергия частицы.
Для стационарного состояния частицы, движущейся со скоростью V<<с вдоль оси х:
![]() (5.23)
(5.23)
где m-масса частицы; Е - полная энергия;U=U(х)-потенциальная энергия частицы;
Ψ(х)-волновая функция, описывающая состояние частицы.
Если частица свободная, то U(х) в уравнении (5.23) равна нулю. Если частица находится в определенном энергетическом состоянии с энергией Е=const, то вероятность ω ее обнаружить в областиΔх или в объемеΔVне зависит от времени. Это состояние частицы называетсястационарным состоянием.Атом в таком состоянии не излучает энергии.
Ч астица
в одномерной прямоугольной потенциальной
яме (ящике). Потенциальной ямой
называется область пространства, в
которой потенциальная энергияUчастицы меньше, чемUза
ее пределами. Пусть яма будет бесконечно
глубокой (рис.5.4). Ширина ямыL.
Частица свободнаяU=0.
астица
в одномерной прямоугольной потенциальной
яме (ящике). Потенциальной ямой
называется область пространства, в
которой потенциальная энергияUчастицы меньше, чемUза
ее пределами. Пусть яма будет бесконечно
глубокой (рис.5.4). Ширина ямыL.
Частица свободнаяU=0.
Рис.5.4
Условия: при х<0 U= ∞; 0<x<LU=0;x>LU= ∞
Уравнение Шредингера для движения частицы вдоль оси х
![]()
Обозначив
![]() через
ω2перепишем уравнение
через
ω2перепишем уравнение
![]()
Решением его
будет
![]() .
Исследуем его.
.
Исследуем его.
При х = 0
![]() ,
т.е. вероятность нахождения частицы за
пределами х0 равна
0 и α = 0.
,
т.е. вероятность нахождения частицы за
пределами х0 равна
0 и α = 0.
При х=L![]() -вероятность
нахождения частицы справа от ямы равна
0. Ψ(L) = 0, если
-вероятность
нахождения частицы справа от ямы равна
0. Ψ(L) = 0, если![]() (n=1, 2, 3,…). Из этого следует,
что решение уравнения (5.23) будет иметь
место лишь при определенных значениях
(n=1, 2, 3,…). Из этого следует,
что решение уравнения (5.23) будет иметь
место лишь при определенных значениях![]() .
Иначе говоря, энергия частицы в
потенциальной яме квантуется. Полагая
разные значенияn, получимэнергетические уровничастицы в
яме (ящике).
.
Иначе говоря, энергия частицы в
потенциальной яме квантуется. Полагая
разные значенияn, получимэнергетические уровничастицы в
яме (ящике).
![]() (n=1, 2, 3,…)
(5.24)
(n=1, 2, 3,…)
(5.24)
Соответствующие значения nназываютсяквантовыми числами.
Определим интервал между энергетическими уровнями:
![]()
Найдем, для
примера
![]() электрона
в атоме (
электрона
в атоме (![]() ,
,![]() )
)![]() nэВ. Сравним с кинетической тепловой
энергией электрона
nэВ. Сравним с кинетической тепловой
энергией электрона![]() эВ
(в атоме
эВ
(в атоме![]() ).
).
Функции
![]() ,
удовлетворяющие уравнению (5.23), называются
нормированнымисобственными функциями
,
удовлетворяющие уравнению (5.23), называются
нормированнымисобственными функциями![]() .
Для нахождения
.
Для нахождения![]() воспользуемся условием нормировки:
воспользуемся условием нормировки:
![]() -
частица с вероятностью ω=1 находится в
ящике (яме)
-
частица с вероятностью ω=1 находится в
ящике (яме)
Среднее значение
![]() ,
умножим на ширину ящикаL,
тогда
,
умножим на ширину ящикаL,
тогда![]() откуда
откуда![]() .
.
Нормированная собственная волновая функция для нашего случая частицы в ящике (яме):
![]() (5.25)
(5.25)
Подставляя (5.25) в уравнение (5.21), находим вероятность нахождения частицы в яме или энергетические уровни по (5.24). График нормированной функциипредставлен на рис.5.5, а, а график вероятности нахождения частицы в пределах 0<х<Lна рис.5.5, б (здесь- комплексно сопряженная функция с).

Рис.5.5
Из графика 5.5, б следует, что частица при квантовом числе n=1 имеет больше вероятности находится в середине ящика, приn=2 равновероятно находиться как в правой так и в левой части ящика и т.д.
Рассмотрим еще один пример, показывающий различие в поведении частицы при рассмотрении с позиций квантовой и классической механики. Пусть частица находится в силовом поле и на ее пути потенциальный барьер высотой U(рис.5.6). Если частица имеет
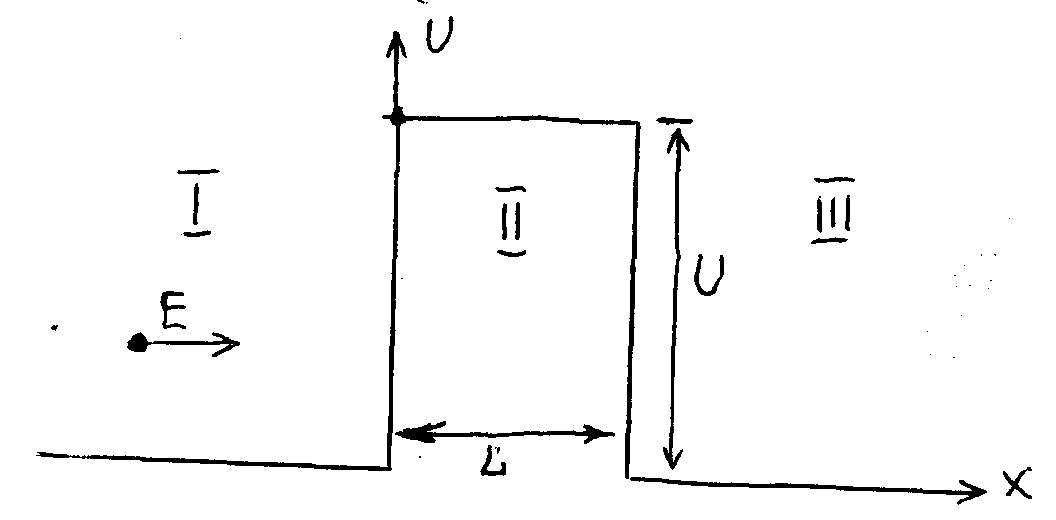
Рис.5.6.
полную энергию Е<Uменьше высоты барьера, то с классической точки зрения она не может преодолеть барьер (пройти через областьII). С позиций квантовой механики она это способна сделать. Неопределенность энергии ΔЕ (см.5.20) частицы может привести к «просачиванию» частицы через барьер, когда изменение кинетической энергии может стать
ΔЕк>U–E
Волновая функция и в области IIψ0.
Таким образом, частицу можно обнаружить в запрещенной для нее с классической точки зрения области (часть частиц отражается от барьера, часть проходит, что подобно тому как свет проходит через границу двух сред). Прохождение частиц сквозь потенциальные барьеры называется туннельным эффектом, а любой барьер характеризуется соответствующимкоэффициентом прозрачности.
Туннельный эффект играет заметную роль при радиоактивном распаде (излучение - частиц ядрами), холодной эмиссии электронов из металлов и др.
Частица с массой m, которая колеблется с собственной частотой0вдоль оси х в яме под действием квазиупругой силыF= -kx, называетсялинейным(одномерным)гармоническим осциллятором.
