4.5. Интерференция волн

Волны от точечного источника распространяются во все стороны (сферические волны). Геометрическое место точек, до которых к некоторому моменту времени дошло колебание, называется фронтом волны. Совокупность точек, колеблющихся в одинаковых фазах, образуетволновуюповерхность.

Волны обладают принципом суперпозиции, т.е. если в среде одновременно распространяются несколько волн, то они распространяются независимо друг от друга. Однако, в тех местах, где одни колебания накладываются на другие колебания, их амплитуды векторно складываются (см. рис.4.2). Наблюдаетсяинтерференция, в результате которой колебания в одних местах усиливаются, в других ослабляются.

Особый интерес представляет тот случай, когда источники испускают волны с одинаковой частотой ω (такие волны называются монохроматическими), одинакового направления и с постоянной во времени разностью фаз Δφ.Волны с одинаковой частотой ω и постоянной разностью фаз называются когерентными.

Вообще реальная волна, излучаемая в течение ограниченного промежутка времени и охватывающая ограниченную область распространения, не является монохроматической. Спектр ее частот имеет конечную ширину . Такую волну можно лишь ограниченное время τ считать монохроматической с частотой ω. Величина τ называетсявременем когерентности. За время τ разность фаз колебаний изменяется на π. Волна с циклической частотой ω и фазовой скоростьюVраспространится за это время на расстояниеd = V · τ, которое называетсядлиной когерентности. Например, для солнечного света, имеющего сплошной спектр в диапазоне частот отдоиd~1мкм. Для лазеров непрерывного действияиd~10³м.

Интерференция от двух когерентных источников

Пусть имеются два когерентных источника S₁иS₂(рис.4.7).

Рис.4.7

Волны от них приходят в точку В, отстоящую от источников на расстояниях у₁и у₂, и интерферируют. Рассмотрим условия наблюдения максимума или минимума в этой точке. Будем для простоты считать, что амплитуда колебаний А₀одинакова,

одинаковы и плоскости колебаний векторов А. Амплитуда в точке В в результате интерференции по принципу суперпозиции волн будет равна сумме:

Из тригонометрии известно, что или в нашем случае:

(4.20)

Величина есть амплитуда вектора А результирующего колебания, полученного при наложении двух волн в точке В (рис.4.7). Она является периодической функцией разности хода лучей Δ =y₂ -y₁и не зависит от времениt.

Очевидно, что амплитуда колебаний вектора А будет максимальнойпри разности хода лучей Δ, равной целому числуmдлин волн или четному числу 2mполуволн, т.е. при:

, (4.21)

так как принимает максимальное значение, а разность фаз колебаний Δφ будет кратным 2π (см. 4.19). Величинуmназывают порядком интерференции (m=0, 1, 2, 3…).

Также можно показать, что при разности хода равной нечетному числу (2m+1) полуволн, т.е. при

(4.22)

колебания ослабляют друг друга. Наблюдается минимум интенсивности.

На экране Э в области, где волны накладываются, будет наблюдаться чередование максимумов и минимумов. Это и есть интерференционная картина (рис.4.7).

Определим координаты х максимумов и минимумов:

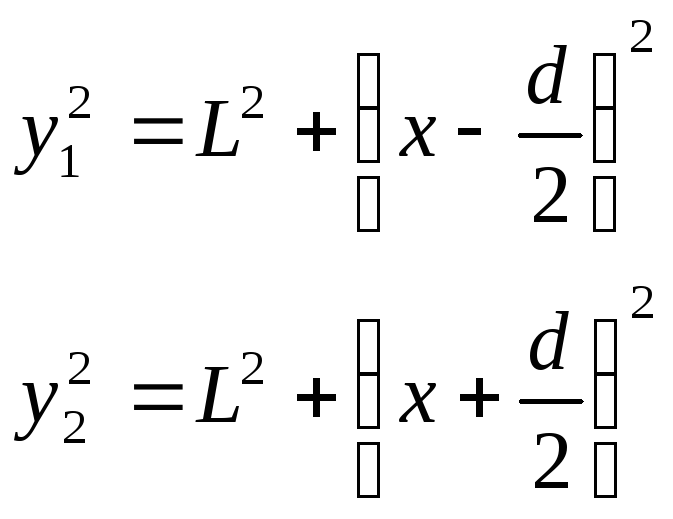
откуда или(4.23)

Полагая, что d<<L, можно считать,дает разность хода волн.

Из (4.23) . С учетом (4.21) для координаты максимума получим:

для минимума

Минимальное расстояние между минимумами (или максимумами) определит ширину интерференционной полосы(рис.4.7)

Пусть S₁иS₂на рис 4.7 являются источниками света. Световым вектором принято считать вектор электрической напряженности. Как показывает опыт, зрительные ощущения, фотоэлектрическое, фотохимическое действия света, вызывают колебания именно электрического вектора Е.Интенсивность I светапропорциональна квадрату амплитуды светового вектора Е².

При наложении световых волн от двух источников:

интенсивность света в точке В (рис.4.7) будет определяться (с учетом 4.20):

На экране Э будут наблюдаться чередующиеся светлые и темные интерференционные полосы разной интенсивности в соответствии с условиями максимума (4.21) или минимума (4.22).

Если свет распространяется не в вакууме, а в среде с оптической плотностью n>1, тооптическая разность хода лучейΔ=y₂n-y₁n=(y₂-y₁)n.

При интерференции происходит перераспределение световой энергии, т.е. закон сохранения энергии не нарушается.

В конце прошлого века сформировалось представление о свете, как имеющемдвойственную природу - волновую и квантовую. Сочетались, казалось бы исключающие друг друга волновые (дифракция, интерференция, поляризация) и квантовые (фотоэффект, эффект Комптона и др.) свойства света.

Естественный свет (например, солнечный) в видимом для человека диапазоне представляет собой электромагнитные волны длиной от 0,4 до 0.76 мкм и частотой 10¹⁵Гц. Волны с длиной меньше 0,4 мкм называется ультрафиолетовыми, а с длиной больше 0,76 мкм - инфракрасными (тепловое излучение). Как было уже рассмотрено (см.п.3.5), в электромагнитной волне электрический вектори магнитный векторколеблются во взаимно перпендикулярных плоскостях поперек направления распространения волны (световые волны - поперечные волны).

Если S₁иS₂-источники естественного света, то на экране Э (рис.4.7) интерференционные светлые полосы будут иметь радужную окраску (из семи цветов), т.к. оптическая разность хода лучей Δ зависит от λ (см.4.21).