Момент сил, действующих на виток с током в магнитном поле

Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле

или(3.58)

α- угол между векторами(направлен по нормали к контуру) и(рис.3.15)

Рис .3.15

Принцип суперпозиции магнитных полей

Каждый ток создает свое магнитное поле независимо от других токов и вектора (или) этих полей складываются геометрически (принцип суперпозиции).

Индукция результирующего магнитного поля от сложения магнитных полей:

;.

Закон Био-Савара-Лапласа и его применение к расчету магнитных полей

Этот закон позволяет определить величину вектора магнитной индукции (или напряженности) в любой точке поля на расстоянииrот проводника с токомI. Так как форма проводника может быть разной, то выделяется на проводнике элементdℓ его длины столь малый, что можно пренебречь его кривизной, и тогда в векторном виде:

или

(3.59)

т.е. индукция dВ магнитного поля, созданная бесконечно малым элементомdℓпроводника с токомIв точке поля на расстоянииrот элемента до этой точки, прямопропорциональна силе токаIдлине элементаdℓи обратно пропорциональнаr²от элемента до точки – это и естьзакон Био-Савара-Лапласа (рис.3.16).

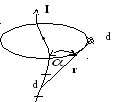
Рис.3.16

Угол α в формуле (3.59) это угол между направлением тока и вектором-радиусом.

Пример: определим магнитную индукцию в центре кругового тока IрадиусомR(рис.3.17)

Рис.3.17

(3.60)

с учетом того, что в формуле (3.59) r=R, α = 90⁰.

Аналогичным образом, интегрируя уравнение (3.59) с учетом формы проводника, получаем:

а) для бесконечно длинного прямого тока:

или(3.61)

где r- кратчайшее расстояние от оси провода до точки, в которой определяется магнитная индукция;

б) для отрезка проводника с током I:

, (3.62)

где α₁и α₂-углы между радиусами-векторами, проведенными в данную точку поля соответственно из начала и конца проводника, и направлением тока;

в) закон полного тока проводимости:

или (3.63)

где ℓ-длина произвольного замкнутого контура в магнитном поле;

n-число витков, охватываемых контуром.

Пользуясь законом полного тока, рассчитаем напряженность Н и индукцию магнитного поля тороида и соленоида. Пусть соленоид имеетNвитков с токомIи длинуL. Проведем замкнутый контур ℓ через середину соленоида так, чтобы он охватывал все витки. Тогда алгебраическая сумма всех охватываемых контуром токов будет:

С другой стороны . Приравняв, получим:

или, (3.64)

Напряженность магнитного поля вне бесконечного длинного соленоида считаем равной нулю. Поле внутри длинного соленоида однородно. Для магнитной индукции поля соленоида имеем:

(3.65)

Формулы (3.64) и (3.65) справедливы и для тороида (кольцевого соленоида радиуса R, где ℓ=2πR). Рис. 3.18

Рис.3.18