Связь между напряженностью и потенциалом электростатического поля

Пусть заряд Qперемещается из точки с потенциалом φ₁в точку с потенциалом φ₂, при этом, согласно (3.17), совершается работа:

A₁₂=Q(φ₁-φ₂)=-Q(φ₂-φ₁)=-QΔφ (3.19)

С другой стороны (см.2.19)

A₁₂=F Δr cos α=E Q Δr cos α

Если направление оси х совпадает с направлением вектора Е, то:

Δr cos α=Δx

и

A₁₂=Q E Δx. (3.20)

Приравнивая правые части (3.19) и (3.20), получим:

E = -Δφ/Δх (3.21)

Это означает, что напряженность поля в данной точке пропорциональна быстроте падания потенциала вдоль линии вектора напряженности. Знак “-” показывает, что вектор Е направлен в сторону убывания потенциала.

Для однородного поля выражение (3.21) принимает вид:

, (3.22)

где d-расстояние вдоль линии напряженности между точками с потенциалами φ₁ и φ₂. Согласно (3.22), размерность напряженности.

В общем случае напряженность определяется как градиент потенциала:

. (3.23)

Идеальный проводник в электростатическом поле

В качестве идеального рассмотрим металлический проводник, помещенный в однородное электрическое поле. Под действием поля свободные электроны начнут перемещаться против поля. В результате (рис.3.8) левая часть проводника зарядится отрицательно, а правая, где будет недоставать электронов, - положительно. Возникающие на проводнике заряды называются индуцированными(само явление - электростатической индукцией).

Перемещение зарядов будет происходить до тех пор, пока внешнее поле не компенсируется собственным полем зарядов внутри проводника. Таким образом,

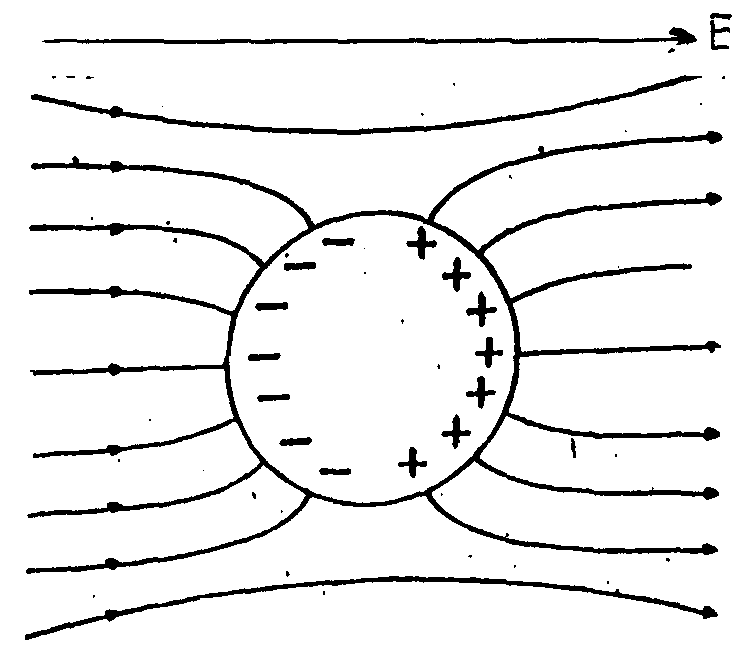
Рис. 3.8

результирующее поле внутри проводника обращается в 0 (Е=0). Отсутствие поля внутри проводника означает согласно (3.22) и (3.23), что все его точки имеют одинаковый потенциал и поверхность проводника является эквипотенциальной. В этом случае силовые линии поля должны быть перпендикулярными к поверхности проводника. Внесенный в однородное внешнее поле проводник искажает его, делая неоднородным.

Индуцируемые заряды располагаются только на поверхности проводника. Если электрическое поле отсутствует внутри сплошного проводника, то очевидно, что оно отсутствует и внутри полости, если такая имеется в проводнике, то есть любой объем, окруженный металлической оболочкой (сплошной или густой сеткой), будет экранирован от внешних электрических полей (электростатическая защита).

При сообщении проводнику избыточного зарядапоследний располагается только по его поверхности с плотностью σ.

Электроемкость уединенного проводника конденсатора

Опыт показывает, что при сообщении заряда Qпроводнику потенциал его изменяется пропорционально на величину φ. Коэффициент пропорциональности

(3.24)

называется электроемкостью(емкостью) проводника.

Единицей емкости является Фарад:.

Потенциал шара радиуса Rсогласно (3.16):

.

Сравнивая с (3.24), получим формулу емкости проводящего шара:

C = 4πε₀ εR. (3.25)

Найдем радиус шара, емкость которого равна 1Ф:

.

Эта величина в 1400 раз больше радиуса Земли. Следовательно, Фарад очень большая единица емкости. Поэтому на практике емкость проводников (конденсаторов) измеряется в мкФ или пФ.

Для увеличения электроемкости проводников в технике используют устройства, называемые конденсаторами. Конденсатор состоит из двух проводников, обычно разделенных диэлектриком. Например, две параллельные плоские пластины, между которыми находится диэлектрик, образуют плоский конденсатор.

Электроемкость конденсатора определяется формулой, аналогичной (3.24):

, (3.26)

где φ₁-φ₂-разность потенциалов между пластинами конденсатора;

σ-поверхностная плотность зарядов на пластинах;

S-площадь пластины.

При наличии диэлектрика между пластинами с диэлектрической проницаемостью ε>1 имеем φ₁- φ₂=Еdили с учетом формулы (3.12):

.

Подставив это значение разности потенциалов в (3.26), получим формулу для емкости плоского конденсатора:

, (3.27)

где d– расстояние между пластинами.

Емкость сферического конденсатора:

С=4π ε ε₀ r₁ r₂/(r₂-r₁), (3.28)

где r₁иr₂-радиусы концентрических сфер.

Емкость цилиндрического конденсатора:

С=2π ε ε₀ ℓ·ℓn·r₁/r₂, (3.29)

где ℓ-длина полых коаксиальных цилиндров радиусамиr₁иr₂.

Для увеличения емкости и варьирования ее возможных значений конденсаторы объединяют в батареи. При параллельном соединении емкость батареи:

(3.30)

При последовательном:

. (3.31)

Энергия системы зарядов.

При формировании системы зарядов затрачивается энергия на преодоление их взаимодействия:

, (3.32)

где φ_i-потенциал в точке, где находится зарядQ_i, созданный всеми зарядами системы кромеQ_i.