7.3 Обратная задача о положении манипулятора

Обратная задача кинематики состоит в следующем: по известной матрице захватного устройства манипулятора в пространстве не­обходимо определить значения обобщенных координат q_i. Анализ уравнений рассмотренных примеров (см. лаб. работу 1) показывает, что поиск коор­динат q_i при известных значениях X , Y и Z не является простым и однозначным, т.к. уравнения нелинейные. Например, для трехзвенного манипулятора (см. лаб. Занятие 3)

(7.1)

Решение обратной задачи о положении сводится к решению нелинейной тригонометрической системы шести уравнений (по числу координат схвата в пространстве) с N неизвестными. Известно, что такие системы могут:

- не иметь ни одного решения; это означает, что заданное положение и ориентация схвата не могут быть достигнуты никаким выбором углов (перемещений) в сочленениях;

- иметь единственное решение;

- иметь более одного решения; это означает что существует несколько (или безконечно много ) конфигураций механизма, обеспечивающих заданное положение схвата.

Умение решать обратную задачу о положении чрезвычайно важно для управления манипулятором. Если программное движение задано в виде траектории его схвата, то для управления сочленениями необходимо обеспечит такие законы изменения координат, чтобы в каждый момент времени в режиме on-line схват находился на заданной траектории. Однако не существует общего метода решения этой задачи в явном виде.

В общем случае для решения поставленной задачи вынуждены прибегать к итерационным методам вычислений. Например, согласно методу Ньютона последова­тельные приближения трех искомых корней α, β, γ системы 3 нелинейных уравнений

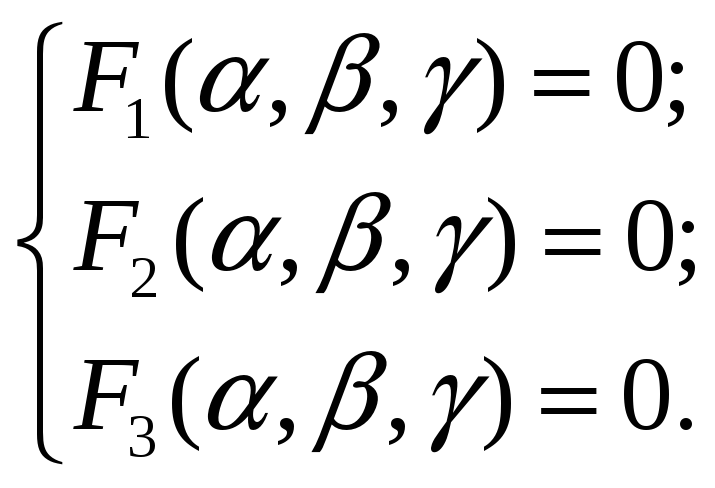
вычисляются по формулам:

(7.2)

где - начальные (k=1) значения корней , определяемые приближенно ( графически, прикидкой и т.п.);

- уточненные значения корней;

J - якобиан рассматриваемой системы уравнений, представляющий собой определитель:

Δ₁ , Δ₂ , Δ₃ - величины, вычисляемые следующим образом

Вычисление корней (2) происходит до момента, когда поправки окажутся меньше принятой точности вычислений.

7.4 Прямая и обратная задачи о скорости манипулятора

Прямая задача о скорости состоит в определении вектора скорости рабочего органа в декартовой системе координат по заданным обобщен­ным координатам звеньев.

Для решения поставленной задачи необходимо продифференцировать по времени систему уравнений, являющуюся решением прямой задачи о положении. Например, для двухзвенного манипулятора:

(7.3)

Полученную систему представим в матричной форме:

(7.4)

где - вектор-столбец декартовых скоростей рабочего органа;

- вектор-столбец обобщенных скоростей манипулятора;

J - матрица Якоби размерности (2 x 2).

Элементами матрицы Якоби являются соответствующие частные производные, входящие в выражения (7.3): пример на лаб. работе 3.

Элементы матрицы Якоби зависят от длин звеньев и значений обобщенных координат, определяющих текущее положение манипу­лятора.

Обратная задача о скорости сводится к нахождению скоростей в подвижных сочленения, при которых обеспечивается движение схвата с заданной линейной и угловой скоростью. Как и обратная задача о положении, решение в явном виде в общем случае не существует. При числе степеней свободы меньше 6

решение сводится к определению обратной матрицы Якоби.

Процедура поиска решения часто является одной из компонент алгоритма управления манипулятором, причем вычислительная сложность процедуры обращения матрицы Якоби определяет эффективность управления в целом.