Лабы по программированию / lab_rab_8_Obr_geom_dan

39

ЛАБОРАТОРНАЯ РАБОТА №8

ОБРАБОТКА ГЕОМЕТРИЧЕСКИХ ДАННЫХ

Цель работы: Освоение методов разработки алгоритмов, составления и отладки программ для обработки геометрических данных.

Требования к выполнению работы:

• Для всех заданий вначале составить блок-схему алгоритма, а затем программу.

• Предусмотреть вывод на печать исходных данных, промежуточных и результирующих данных.

• В работе необходимо для задания координат точек на плоскости использовать два одномерных или один двумерный массив.

• Продемонстрировать работу программы на нескольких наборах исходных данных таким образом, чтобы получить различные варианты решения задачи.

• В отчете привести все формулы, согласно которым построен алгоритм и разработана программа.

Теоретические положения

Положение точки на плоскости определяется двумя координатами - x и y.

Для решения задач по обработке множества точек на плоскости необходимо описать координаты точек, используя один из способов:

1. Описать два одномерных массива для записи координат точек на плоскости;

float x[50], y[50];

2. Описать один двухмерный массив

float x[50][2];

Первый столбец – это координаты точек по оси x, второй – координаты по y.

В геометрических задачах могут потребоваться следующие формулы:

• расстояние между двумя точками i и j: d =

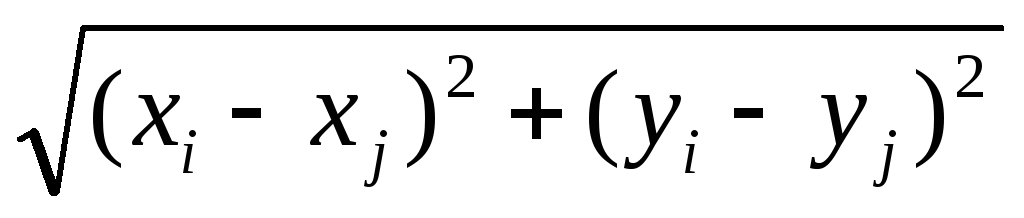
• уравнение прямой, проходящей через две заданные точки:

(y - y1)(x2 - x1) =(x - x1)(y2 - y1).

• расстояние от точки М (х0, у0) до прямой Ах + Ву + С = 0 :

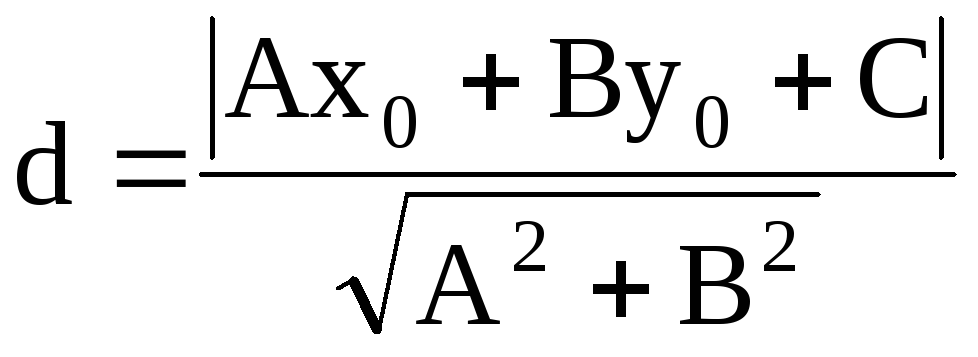
• уравнение окружности с центром в начале координат: x² + y² = r²

• уравнение окружности с центром в точке (x0;y0):

(x - x0)² + (y - y0)² = r²

• длины сторон треугольника a, b и c нельзя задавать произвольно, они связаны следующими неравенствами:

a < b + c ; b < c + a; c < a + b

• площадь треугольника вычисляется по формуле Герона:

S=p(p−a)(p−b)(p−c),

где р- полупериметр треугольника.

;

• многоугольник называют выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Для нахождения площади многоугольника можно использовать следующий алгоритм, при котором производится разбиение выпуклого многоугольника на треугольники. Пусть некоторый многоугольник задан набором координат своих вершин

P0 = (x0, y0), P1 = (x1, y1), ..., Pn = (xn, yn)

При этом будем полагать, что вершины пронумерованы по часовой стрелке. В случае если многоугольник выпуклый, задача нахождения разбиения тривиальна - можно взять набор диагоналей выходящих из какой-либо вершины. Далее находим сумму площадей полученных треугольников по формуле Герона.

Пример.

На плоскости заданы множество точек М и окружность. Выбрать из множество точек М две различные точки так, чтобы наименьшим образом различались количества точек в окружности, лежащие по разные стороны от прямой, проходящей через эти точки.

Решение задачи можно разбить на несколько этапов.

1) Выборка двух точек из n точек без повторения реализована циклами:

for (i= 0; i< n-1;i++)

for (j= i+1; j< n;j++)

2) Перебор всех оставшихся точек и определение факта, лежит ли проверяемая точка внутри круга.

Условие (x-x0)²+(y-y0)² < r² означает, что расстояние от точки (x, y) до центра круга (x0, y0) меньше его радиуса и соответственно точка лежит внутри круга.

3) Определение места расположения точки относительно прямой и подсчет количества точек выше и ниже прямой. Чтобы определить, где находится точка по отношению к прямой, подставляем её координаты (x, y) в уравнение прямой, проходящей через две другие точки множества с координатами (x1,y1) и (x2,y2) соответственно.

Уравнение прямой через две точки:

(x1-x2)/(y1-y2)=(x-x1)/(y-y1) Следовательно,

y=((x1-x2)/(y1-y2))/ (x-x1)+y1

Подставляем x и y: если y=((x1-x2)/(y1-y2))/ (x-x1)+y1, то точка находиться на прямой;

если y>((x1-x2)/(y1-y2))/ (x-x1)+y1, то точка находиться выше прямой;

если y<((x1-x2)/(y1-y2))/ (x-x1)+y1, то точка находиться ниже прямой.

Может оказаться так, что точки имеют одинаковую координату по x, поэтому в уравнении получиться деление на ноль. Поэтому перед подстановкой в неравенство необходимо сравнить абсциссы точек, и если они равны, все точки будут лежать либо справа либо слева от прямой.

После каждого сравнения увеличиваем счётчики high - для подсчёта точек выше прямой или справа и счётчик low - для подсчёта точек ниже прямой или, соответственно, слева от неё.

Каждый раз, найдя решение лучше предыдущего, сохраняем его в переменных res, t1, t2.

Текст программы.

#include <stdio.h>

#include <conio.h>

n=5; /*число точек множества*/

int i,j=0,t,r,x0,y0,high,low,res;

int M[20][2];

int t1,t2;/*в них запишем номера двух точек, - решение задачи*/

x0= 0; /*x-координата центра окружности*/

y0= 0; /*y-координата центра окружности */

r= 10; /*радиус окружности */

randomize();

/*координаты точек задаём случайным образом*/

for (i=0;i<n;i++)

{

M[i][0]= random(10)-1;

M[i][1]= random(10)-5;

}

/*вывод координат точек на экран*/

for (i=0;i<n;i++)

printf("\n x=%d y=%d \n", M[i][0], M[i][1]);

res= n+1; /*инициализация просто большим числом*/

for (i=0;i<n;i++)

{

if((M[i][0]-x0)*(M[i][0]-x0)+(M[i][1]-y0)*(M[i][1]-y0) > r*r)

j++;/*в j считаем точки вне окружности */

}

if (j == n-1) {printf("\n Все точки вне круга \n");

exit(1);

}

/*выборка двух точек из n без повторений*/

for (i=0;i<n-1;i++)

{for (j=i+1;j<n;j++)

{high= 0;

/*начальные условия: high - для подсчёта точек выше прямой или справа*/

low= 0; /*low - для подсчёта точек ниже и,

соответственно, слева прямой */

for (t=0;t<n;t++) /*перебираем все точки */

{

if((M[t][0]-x0)*(M[t][0]-x0)+(M[t][1]-y0)*(M[t][1]-y0) < r*r) /*которые внутри окружности */

{

if ((M[i][0]==M[j][0])&&(M[t][0] > M[i][0])) high++; /*прямая||Oy, точки справа*/

if ((M[i][0]==M[j][0]) && (M[t][0] < M[i][0])) low++; /*прямая||Oy, точки слева*/

if (M[i][0] != M[j][0])

{

/*прямая не||Oy, подставляем координаты в уравнение прямой */

if (M[t][1]>((M[i][1]-M[j][1])/

(M[i][0]- M[j][0]))*(M[t][0]-M[i][0])+M[i][1])

high++;

if (M[t][1]<((M[i][1]-M[j][1])/

(M[i][0]-M[j][0]))*(M[t][0]-M[i][0])+M[i][1])

low++;

}}

}

if (res > abs(high - low))

{

res= abs(high - low);

/*вычисляем разницу high - low по модулю, если этот результат меньше результата, полученного ранее, эти две точки будут новым решением */

t1= i;

t2= j;

}

} }

printf("\n");

/*вывод разницы в количестве точек по разные стороны от прямой на экран */

printf("high=%d low=%d res=%d t1=%d t2=%4d\n",

high,low,res,t1,t2);

/*вывод самих точек на экран */

printf("%4d %4d\n", M[t1][0],M[t1][1]);

printf("%4d %4d", M[t2][0],M[t2][1]);

gets;

}

Условие заданий:

1. Заданы окружность с помощью координат центра и радиуса. Определить, в каких четвертях она расположена.

2. Заданы координаты квадрата и координаты 10 точек. Определить какая из точек, к какой вершине квадрата лежит ближе всего.

3. Заданы две пересекающиеся прямые, с помощью 4 точек. Найти координаты точки пересечения и расстояния от нее до заданных точек.

4. Заданы две пересекающиеся прямые, с помощью 4 точек. Найти площади двух смежных треугольников, лежащих между этими прямыми.

5. Заданы две пересекающиеся прямые, с помощью 4 точек. Определить площадь наибольшего из треугольников, полученных при пересечении этих прямых.

6. Заданы координаты 10 точек. Найти длину наибольшего отрезка, соединяющего эти точки.

7. Заданы координаты 10 точек. Найти точку, имеющую наибольшее расстояние до начало координат, и величину этого расстояния.

8. Заданы координаты 16 точек. Найти длину ломаной, соединяющей точки в порядке номеров.

9. Заданы координаты 12 точек. Найти наибольшую площадь круга, построенного по двум точкам – центр и точка на окружности.

10. Заданы координаты 28 точек. Разделить их на 4 части: лежащие в различных четвертях координатной плоскости.

11. Заданы координаты 20 точек, лежащих в первой четверти. Разделить их на две части: лежащие выше биссектрисы первой четверти и ниже ее.

12. Заданы координаты 20 точек. Разделить их на две части: лежащие выше оси абсцисс и ниже ее.

13. Заданы окружность, с помощью координат центра и радиуса и координаты 20 точек. Разделить точки на две части: лежащие внутри окружности и вне нее.

14. Задана окружность, с помощью координат центра и радиуса. Определить, лежит ли она полностью в первой четверти.

15. Заданы координаты 6 точек. Определить площадь многоугольника.

16. Заданы квадрат, с помощью координат четырех углов, стороны которого параллельны осям, и координаты 10 точек. Найти ее точки, которые лежат внутри этого квадрата.

17. Заданы окружность, с помощью координат центра и радиуса, и квадрат, с помощью координат вершин. Определить лежит ли квадрат внутри окружности или вне нее.

18. Заданы окружность, с помощью координат центра и радиуса, и прямая, с помощью координат 2 точек. Определить пересекаются ли фигуры.

19. Заданы окружность, с помощью координат центра и радиуса и квадрат, с помощью координат вершин. Определить, пересекаются ли фигуры.

20. Заданы прямоугольник, с помощью координат четырех углов, стороны которого параллельны осям и координаты 15 точек. Найти те точки, которые лежат за пределами этого прямоугольника.

21. Заданы координаты 5 точек. Определить площадь многоугольника.

22. Даны координаты точек трех прямых. Выяснить, можно ли на них построить треугольник.

23. Заданы окружность, с помощью координат центра и радиуса и треугольник, с помощью координат вершин. Определить, лежит ли треугольник внутри окружности.

24. Заданы окружность, с помощью координат центра и радиуса и шестиугольник, с помощью координат вершин. Определить, лежит ли шестиугольник внутри.

25. Заданы окружность, с помощью координат центра и радиуса. Определить, лежит ли окружность полностью в первой четверти.

26. Заданы квадрат, с помощью координат четырех углов, стороны которого параллельны осям и координаты 10 точек. Разделить все точки на 2 части, те точки, которые лежат за пределами квадрата и те, которые лежат внутри квадрата.