
- •Курс лекций
- •П р е д и с л о в и е
- •Элементы линейной алгебры Лекция № 1. Тема 1 : Определители
- •1.1. Определители второго и третьего порядков
- •1.2. Основные свойства определителей
- •1.3. Вычисление определителей
- •Лекция № 2. Тема 2 : Системы линейных алгебраических уравнений
- •2.1. Правило Крамера
- •Лекция № 3. Тема 3 : Матрицы
- •3.1. Основные виды матриц
- •3.3. Обратная матрица
- •3.4. Решение систем линейных уравнений с помощью обратной матрицы
- •Векторная алгебра Лекция № 4. Тема 1 : Векторы
- •1.1. Определение вектора
- •Лекция № 5.
- •1.4. Способы задания векторов
- •1.5. Деление отрезка в заданном отношении
- •Тема 2: Скалярное произведение
- •2.1. Скалярное произведение двух векторов и его основные свойства
- •2.2. Скалярное произведение векторов, заданных координатами
- •2.3. Длина вектора. Угол между двумя векторами.
- •Лекция № 6. Тема 3 : Векторное произведение
- •3.1. Векторное произведение двух векторов и его основные свойства
- •3.2. Векторное произведение векторов, заданных своими координатами
- •3.3.* Механический смысл векторного произведения
- •Тема 4 : Смешанное произведение
- •4.1. Смешанное произведение и его основные свойства
- •4.2. Смешанное произведение векторов, заданных своими координатами
1.2. Основные свойства определителей
Все рассмотренные свойства легко проверить непосредственно на примере определителей третьего порядка, хотя они справедливы и в общем случае.
1. При замене столбцов строками с тем же номером (при транспони-ровании) определитель своего значения не меняет, т.е. строки и столбцы у определителя равноправны.
Таким образом, требуется доказать равенство
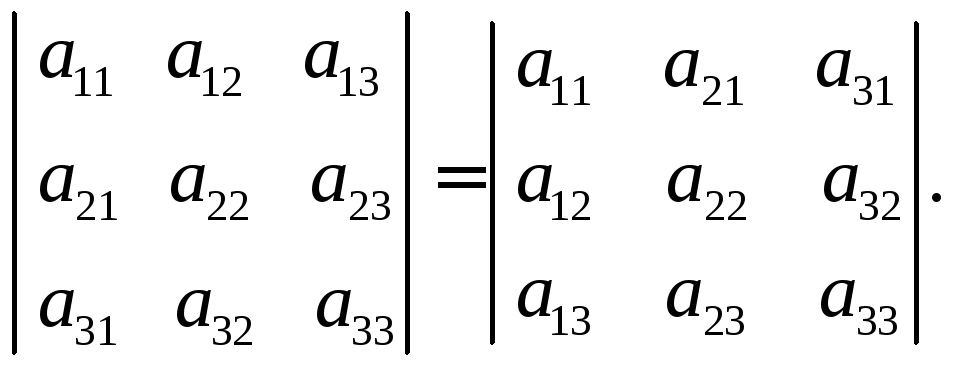
2. Определитель, содержащий строку (столбец) из нулей, равен нулю.
Действительно, так как в этом случае каждый член определителя содержит множителем элемент этой строки (или столбца), равный нулю.
3. При перестановке двух строк (столбцов) определитель меняет знак.
Доказывается непосредственно, как и свойство 1.
4. Определитель, содержащий две равные строки (столбца), равен нулю.
Сделаем перестановку
этих строк. Тогда из свойства 3 получим
![]()
5. Общий множитель всех элементов строки (столбца) можно выносить за знак определителя.
Действительно, это можно сделать, так как этот множитель содержится в каждом члене определителя.
6. Определитель, содержащий две пропорциональные строки (столбцы) равен нулю.
Доказательство этого свойства следует из свойств 45.
7. Если все элементы строки (столбца) представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, каждый из которых имеет строку (столбец) из соответствующих слагаемых элементов.
Например,
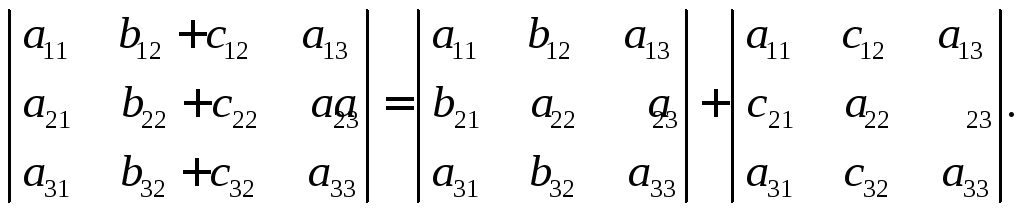
Доказывается непосредственно, исходя из определения определителя третьего порядка.
8. Если к элементам некоторой строки (столбца) прибавить соответст-вующие элементы другой строки (столбца), умноженные на одно и то же число, то определитель своего значения не изменит.
Доказательство следует из свойств 67.
1.3. Вычисление определителей
Определение 3.
Алгебраическим дополнением
![]() некоторого элемента
некоторого элемента![]() данного определителя называется
определитель, получаемый при вычеркивании
из данного определителя строки и
столбца, содержащих этот элемент, и
взятый со знаком
данного определителя называется
определитель, получаемый при вычеркивании
из данного определителя строки и
столбца, содержащих этот элемент, и
взятый со знаком![]() .
.
Пример 1.
Найти
![]() и
и![]() определителя
определителя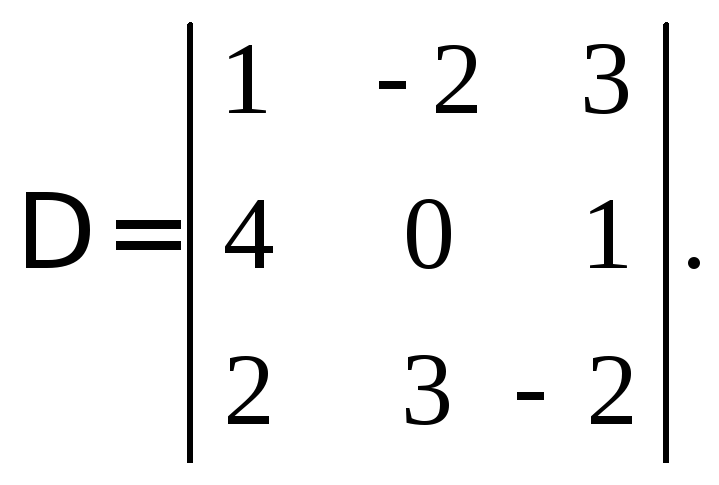

Тогда имеет место следующая
Теорема. Пусть в некотором определителе произвольно выбрана строка (столбец). Тогда сумма произведений элементов этой строки (столбца) на их алгебраические дополнения равна значению определителя.
Например, для
строки
![]()
для
столбца
![]()
Приведенные формулы
легко доказать непосредственно для
любых
![]() .
.
Замечание 1. Из теоремы видно, что вычисление определителя третьего порядка сводится к вычислению определителей второго порядка. Анало-гично, исходя из этого факта, можно получить определение определителя п-го порядка через определитель (п 1)-го порядка.
Например, для определения определителя 4-го порядка имеет место формула
![]() (6)
(6)
где
![]()
определители
третьего
порядка.
определители
третьего
порядка.
Замечание 2. Используя свойство 8 определителей, можно упростить их вычисление, делая в строке (столбце) все элементы равные нулю, кроме одного.
Пример 3.
Вычислить определитель
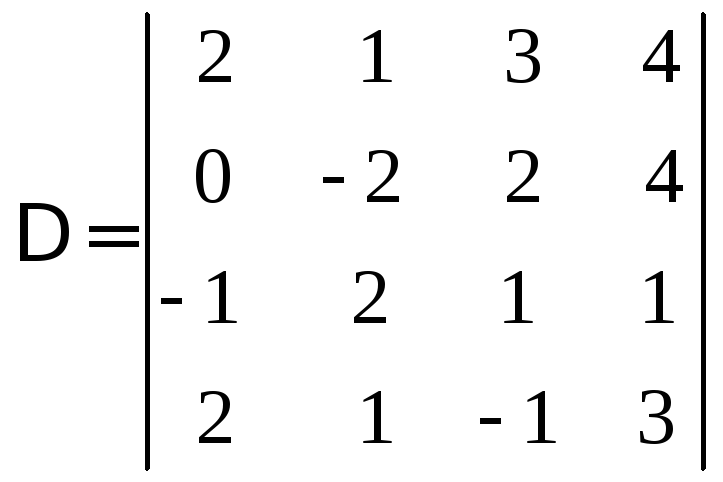 .
.
1 шаг: Прибавим ко 2-ому столбцу третий столбец;
2 шаг: Прибавим к 4-ому столбцу 3-й столбец, умноженный на 2:

В результате во
2-й строке остался один элемент
![]() ,
неравный нулю.
,
неравный нулю.
Воспользуемся формулой (6):

