3.2. Производная векторной функции
Дадим приращение
аргументу t.
В результате векторная функция
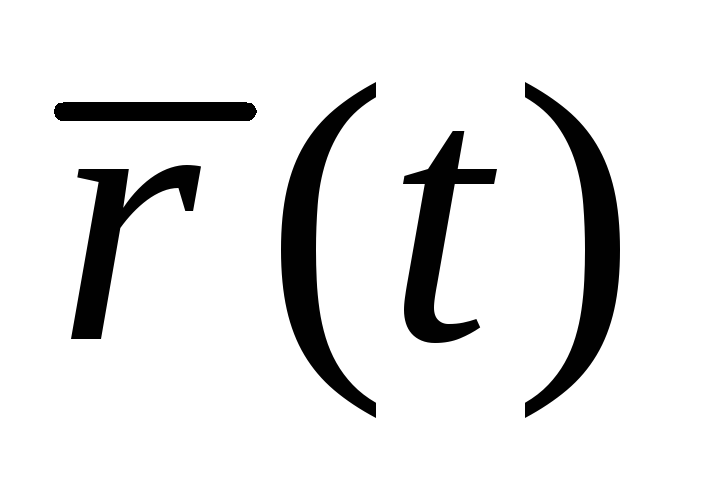 получит приращение
получит приращение
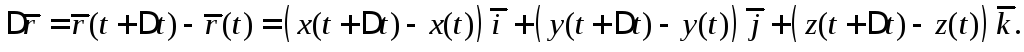
Рассмотрим отношение
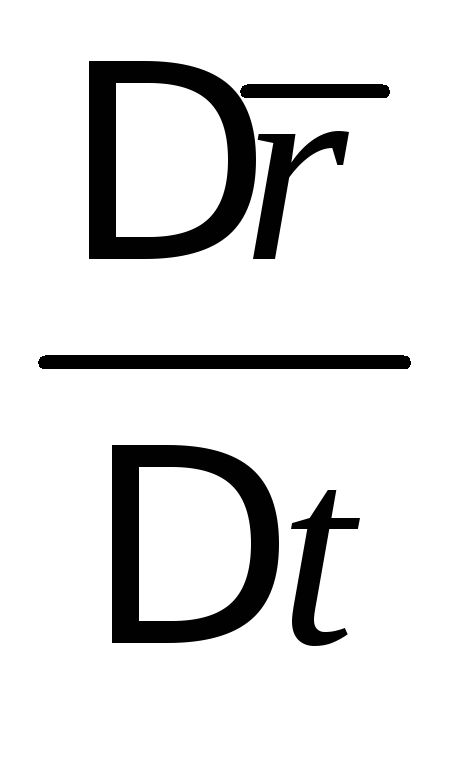 .
Если функции
.
Если функции являются дифференцируемыми, то
являются дифференцируемыми, то

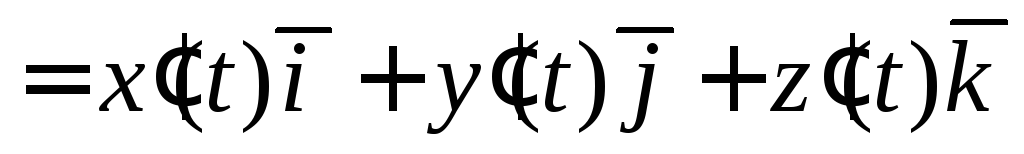 .
(2)
.
(2)
Формула (2) определяет
производную векторной функции скалярного
аргумента. Модуль этого вектора равен
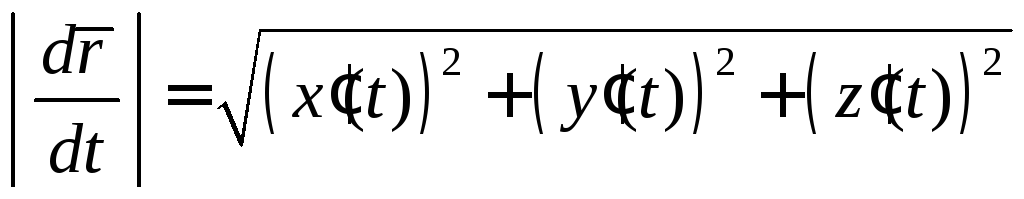 .
.
Выясним геометрический
смысл производной.

М

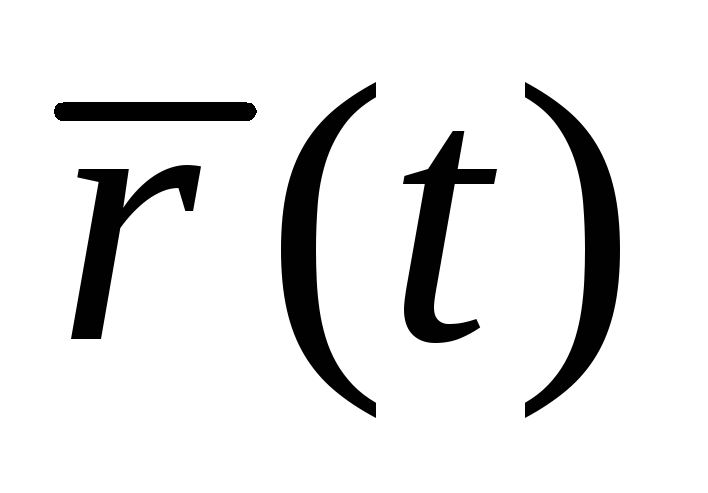
М1
О

Из рисунка видно,
что при
 ,
т.е. производная имеет направлениекасательной.
Нормалей
к пространственной кривой в данной
точке можно провести бесконечное
множество – все они лежат в плоскости,
которая называется нормальной
плоскостью.
Исходя из геометрического смысла
производной, получаем уравнение
касательной
,
т.е. производная имеет направлениекасательной.
Нормалей
к пространственной кривой в данной
точке можно провести бесконечное
множество – все они лежат в плоскости,
которая называется нормальной
плоскостью.
Исходя из геометрического смысла
производной, получаем уравнение
касательной
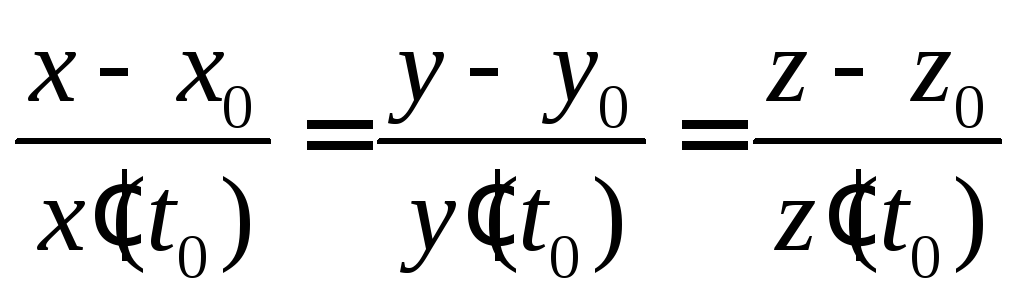
и уравнение
нормальной плоскости
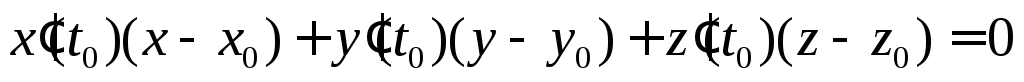 .
.
Замечание 3.
Из определения производной следует,
что правила её нахождения такие же,
как идля
скалярной функции одного переменного.
Аналогично, как
и для плоской линии, вводится понятие
её кривизны.
Формула для
вычисления кривизны пространственной
линии имеет вид
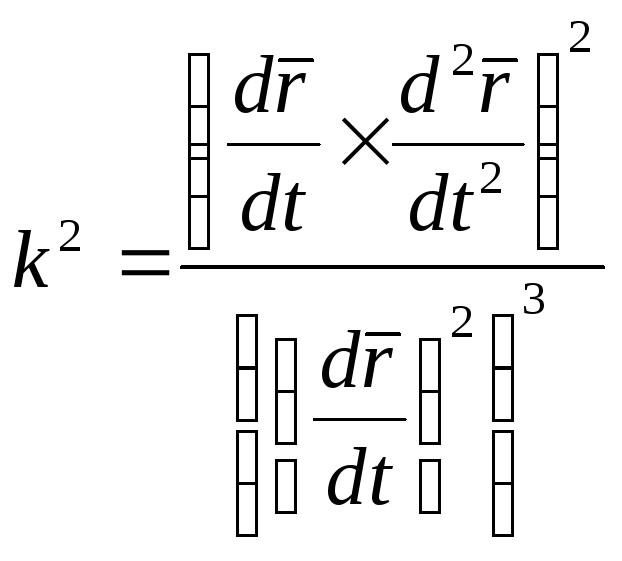 .
.
Пример 2.
Показать, что если
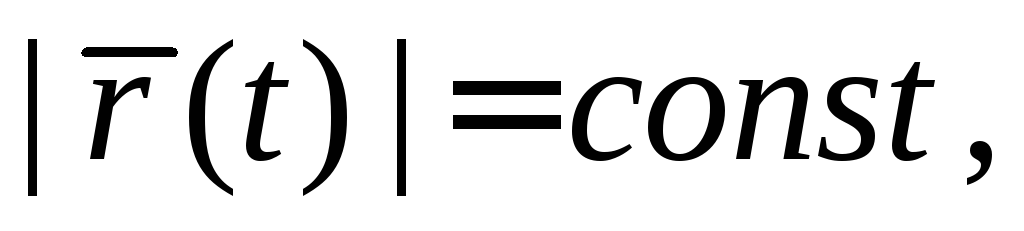 то
то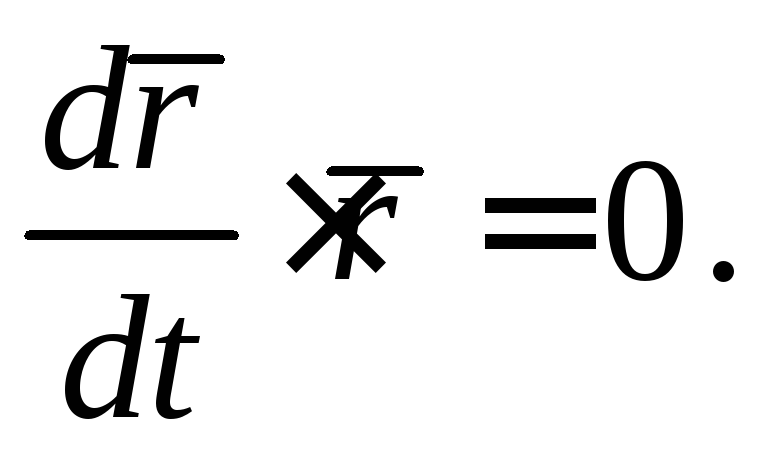
Действительно,
так как
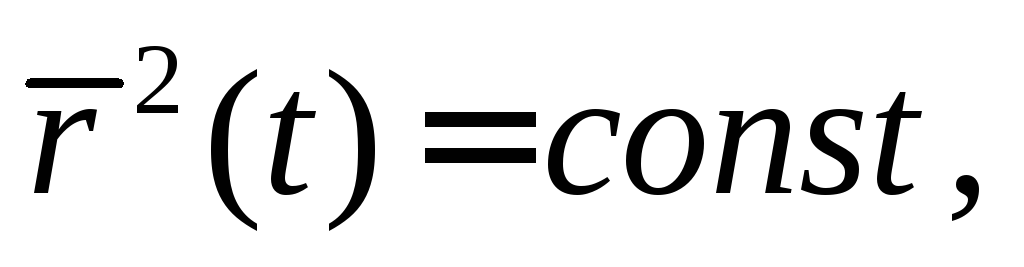 то дифференцируя, получаем
то дифференцируя, получаем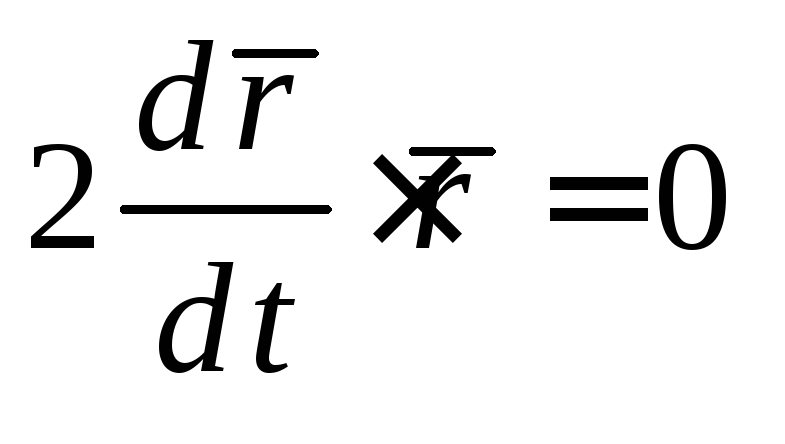 ,
ч.т.д.
,
ч.т.д.
Пример 3.
Составить уравнение касательной,
нормальной плоскости и вычислить
кривизну винтовой линии в точке
 .
.
Вычислим значения
функций и их производных в соответствующей
точке:
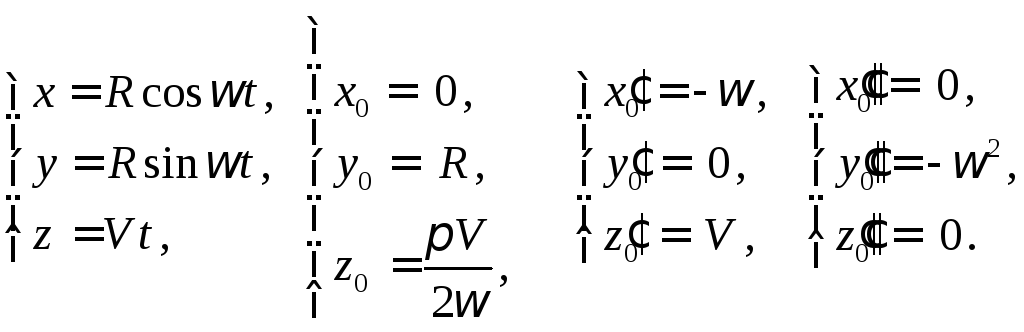
Составим уравнение
касательной
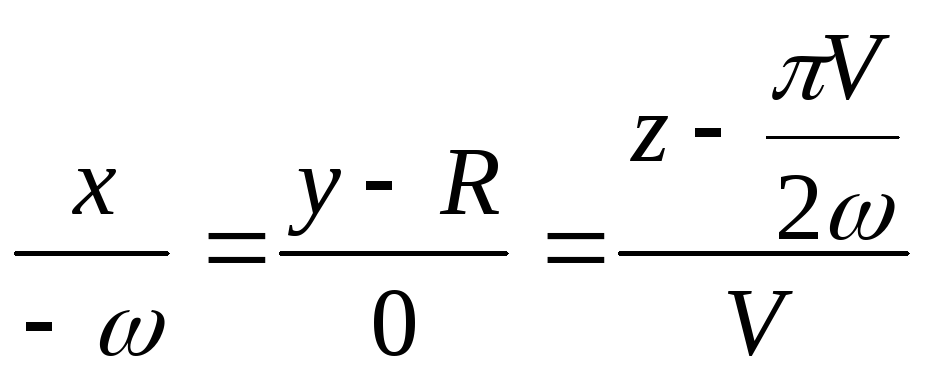
и нормальной
плоскости

Найдём векторное
произведение векторов
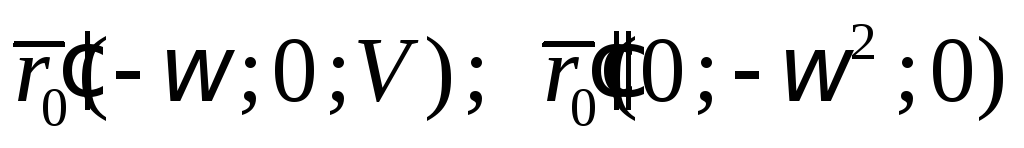
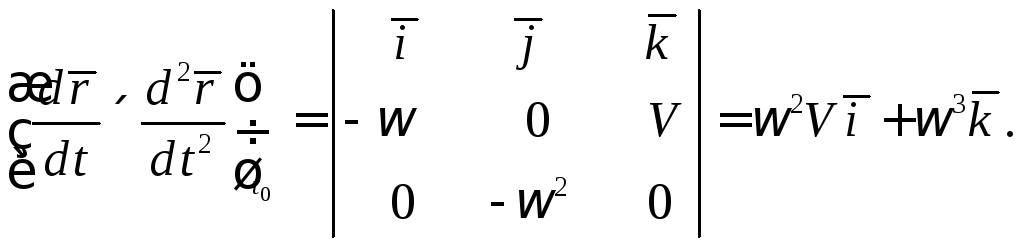
Тогда
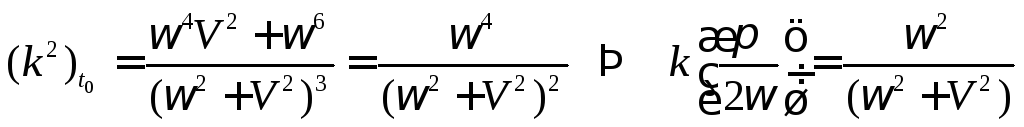 .
.



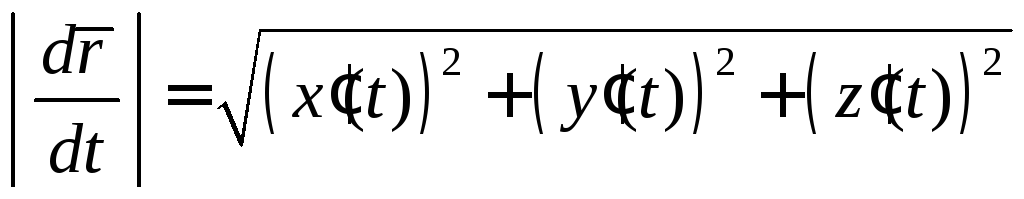 .
.
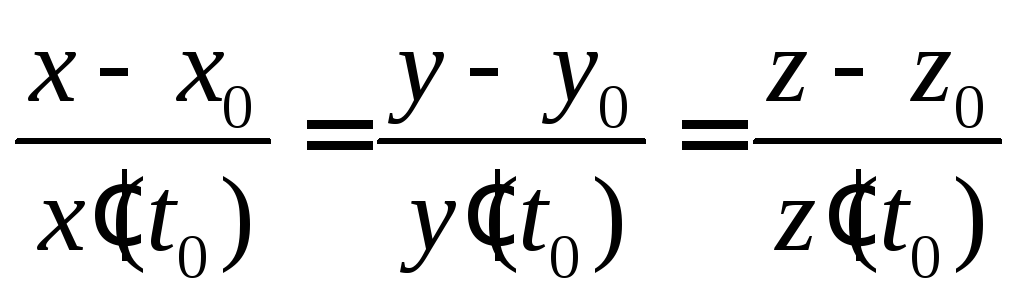
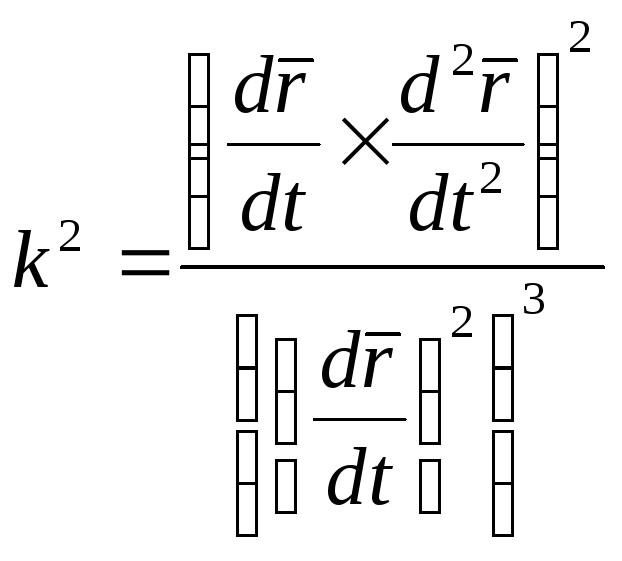 .
.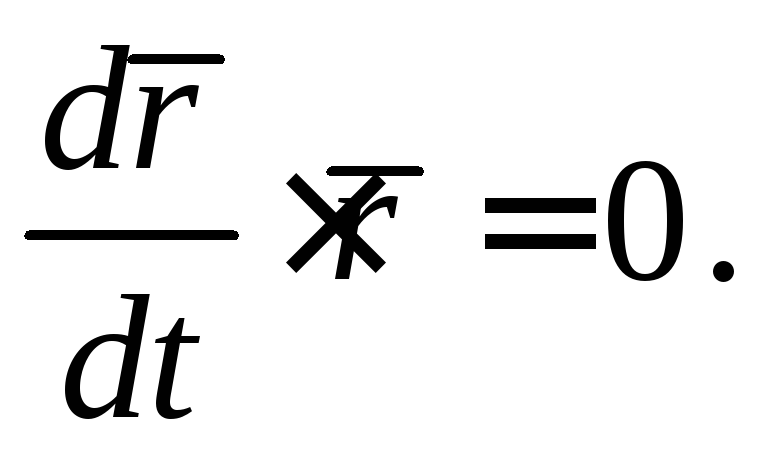
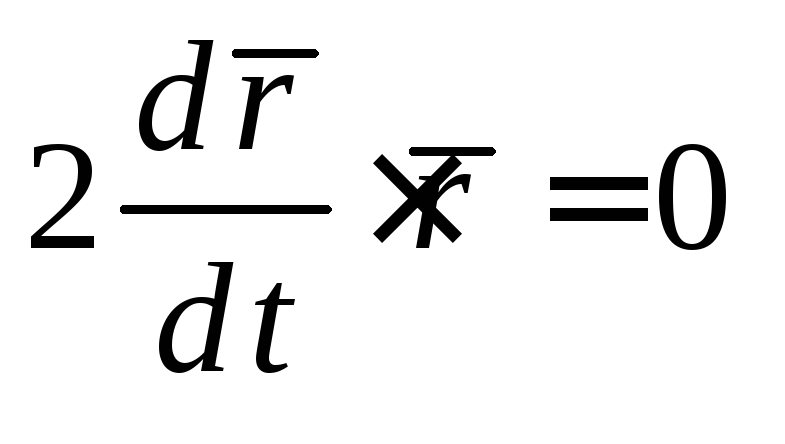 ,
ч.т.д.
,
ч.т.д.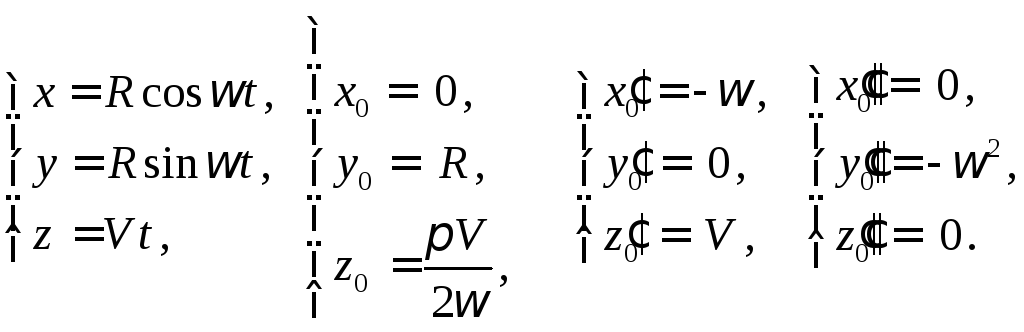
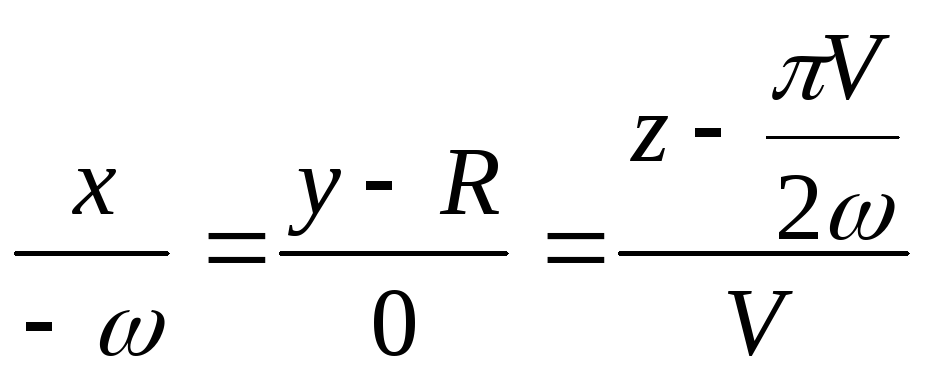

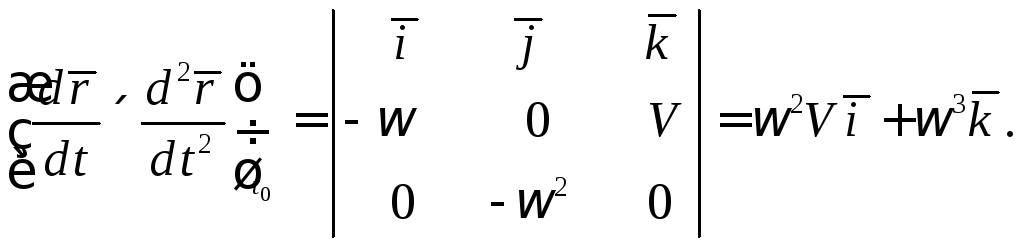
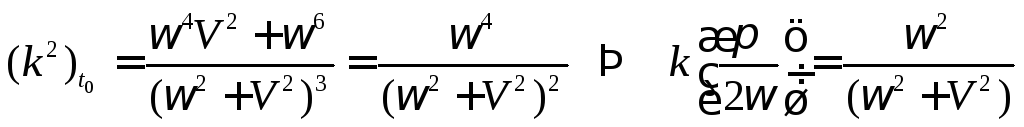 .
.