
- •Аналитическая геометрия Лекция № 7. Тема 1 : Линии на плоскости и их уравнения
- •1.1. Линии и их уравнения в декартовой системе координат
- •1.2. Параметрические уравнения линий
- •1.3. Уравнение линии в полярной системе координат
- •1.4. Преобразование системы координат.
- •Лекция № 8. Тема 2 : Прямая линия на плоскости
- •2.1. Уравнения прямой линии
- •2.2. Угол между двумя прямыми
- •2.3. Взаимное расположение двух прямых
- •2.4. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой, проходящей через точку с заданным угловым коэффициентом
- •2.6. Расстояние от точки до прямой
- •Лекция № 9. Тема 3 : Линии второго порядка
- •3.1. Эллипс
- •3.2. Гипербола
- •10.3. Парабола
- •10.4. Классификация линий второго порядка
- •Лекция № 10. Тема 4 : Плоскость
- •4.1. Уравнение плоскости. Построение плоскости
- •4.2. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору
- •4.3. Уравнение плоскости, проходящей через три заданные точки
- •4.4. Угол между двумя плоскостями
- •4.5. Расстояние от точки до плоскости
- •Тема 5 : Прямая в пространстве
- •5.1. Уравнения прямой
- •Лекция № 11.
- •5.2. Уравнение прямой, проходящей через две точки
- •5.3. Угол между двумя прямыми
- •5.4. Расстояние от точки до прямой
- •5.5. Угол между прямой и плоскостью
- •5.6. Пересечение прямой с плоскостью
- •Лекция № 12. Тема 6 : Поверхности
- •6.1. Уравнение поверхности
- •6.2. Поверхности второго порядка
Лекция № 12. Тема 6 : Поверхности
6.1. Уравнение поверхности
Аналогично, как и
для случая линии на плоскости, уравнение
поверхности – это уравнение с тремя
переменными
![]() ,
которому удовлетворяют координаты
любой точки поверхности и не удовлетворяют
координаты никакой другой точки, не
лежащей на поверхности. Верно и обратное,
т.е.
каждое
уравнение вида
,
которому удовлетворяют координаты
любой точки поверхности и не удовлетворяют
координаты никакой другой точки, не
лежащей на поверхности. Верно и обратное,
т.е.
каждое
уравнение вида
![]() ,
(1)
,
(1)
вообще говоря, определяет некоторую поверхность в пространстве. Если уравнение (1) не удовлетворяется координатами ни одной точки, то говорят, что оно определяет мнимую поверхность. В дальнейшем такие случаи рассматривать не будем.
Пример 1.
Составить уравнение сферы радиуса R
с центром в точке
![]() .
.
Пусть
![]()
текущая точка сферы, тогда для вектора
текущая точка сферы, тогда для вектора
![]() с координатами
с координатами![]() должно выполняться условие
должно выполняться условие
![]() ,
,
которое и является искомым уравнением сферы.
Р ассмотрим
один из часто встречающихся случаев –поверхности
вращения.
Пусть, например, в плоскости Oyz
z
ассмотрим
один из часто встречающихся случаев –поверхности
вращения.
Пусть, например, в плоскости Oyz
z
задана некоторая линия, уравнение которой М1
![]() .
Найдём уравнение поверхности,
M
.
Найдём уравнение поверхности,
M
![]()
полученной вращением этой линии вокруг
оси Oz. N
Возьмём произвольную
точку
![]() O
у
O
у
этой поверхности и проведём плоскость,
перпендикулярную оси Oy. Очевидно, что х
в сечении получим окружность с центром
в точке N.
Тогда
![]() .
С другой стороны, радиус этой окруж-ности
.
С другой стороны, радиус этой окруж-ности![]() ,
где точкаМ1
принадлежит линии
,
где точкаМ1
принадлежит линии
![]() .
Следовательно, для всех точек поверхности
вращения должно выполняться уравнение
.
Следовательно, для всех точек поверхности
вращения должно выполняться уравнение
![]()
Аналогично можно получать уравнения поверхностей вращения относительно других координатных осей.
Пример 2.
Найти уравнение поверхности, образованной
вращением эллипса
 в плоскостиOxy
вокруг оси Ox.
в плоскостиOxy
вокруг оси Ox.
Для этого случая
нужно провести замену
![]() в уравнении эллипса. Тогда получим
уравнение
в уравнении эллипса. Тогда получим
уравнение ,
которое определяет поверхность так
называемогоэллипсоида
вращения.
,
которое определяет поверхность так
называемогоэллипсоида
вращения.
6.2. Поверхности второго порядка
Пусть в некоторой ДСК задана поверхность, определяемая уравнением второй степени
![]() (2)
(2)
где коэффициенты
![]() одновременно не равны нулю. Эта поверхность
называется поверхностью второго
порядка.
одновременно не равны нулю. Эта поверхность
называется поверхностью второго
порядка.
Рассмотрим частные случаи уравнения (2):
1.
Эллипсоид.
Его каноническое уравнение
![]() .
.
Чтобы составить
представление об этой поверхности,
проведём сечения плоскостями, параллельными
координатным плоскостям. Предварительно
заметим, что при замене
![]() уравнение эллипсоида не изменяется –
это означает, что эта поверхность
симметрична относительно координатных
плоскостей. Например, пересекая эллипсоид
плоскостями
уравнение эллипсоида не изменяется –
это означает, что эта поверхность
симметрична относительно координатных
плоскостей. Например, пересекая эллипсоид
плоскостями![]() ,
получаем в сечениях эллипсы вида
,
получаем в сечениях эллипсы вида
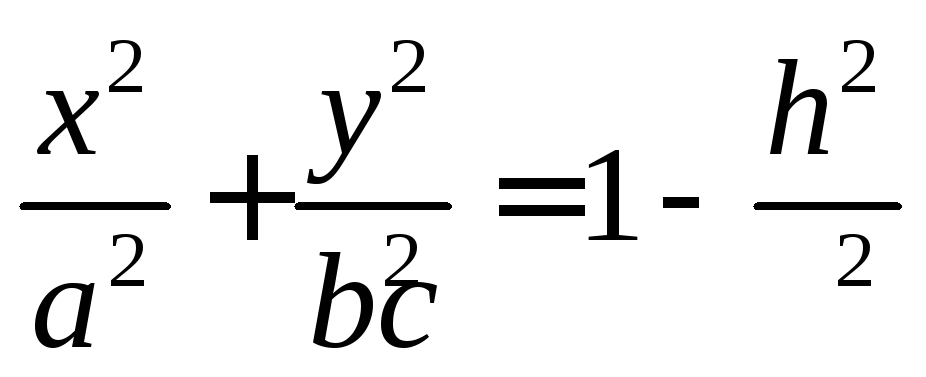
с полуосями
полуосями![]() .
Отсюда видно, что самый большой эллипс
получается в сечении
.
Отсюда видно, что самый большой эллипс
получается в сечении
![]() а при увеличении h
эллипсы уменьшаются, вырождаясь в точку
при
а при увеличении h
эллипсы уменьшаются, вырождаясь в точку
при
![]() .
Аналогичная картина будет в сечениях
плоскостями
.
Аналогичная картина будет в сечениях
плоскостями![]() .
На основании таких исследований можно
определить вид эллипсоида.
.
На основании таких исследований можно
определить вид эллипсоида.
z
c
a
b b y
a
x c
Так же можно получить вид следующих поверхностей:
2 .Однополостный
гиперболоид
z
.Однополостный
гиперболоид
z

y
x
3. Двуполостный гиперболоид

![]() z
z
y
x
4. Эллиптический параболоид
![]() .
.

z
x y
5. Гиперболический
параболоид
![]() .
.

z
x
y

6. Конус
 z
z
y
x
7. Эллиптический
цилиндр


z
y
x
8. Гиперболический
цилиндр

9 .Параболический
цилиндр
z
.Параболический
цилиндр
z
![]() .
.
y
x
10. Пара пересекающихся плоскостей
![]() или
или
 .
.
11. Пара
параллельных плоскостей
![]() или
или
![]() .
.
12. Пара
совпадающих плоскостей
![]() .
.
13. Точка

Аналогично, как и для случая линий второго порядка, имеет место
Теорема. Для любого уравнения (2) поверхности второго порядка существует такая ДСК, в которой уравнение принимает один из видов (1-13).
Пример 3.
Найти точки пересечения прямой
![]() с однополостным гиперболоидом
с однополостным гиперболоидом
Прямую
представим
параметрическими
уравнениями
 Под-
Под-
ставим
![]() в уравнение гиперболоида, получим
уравнение для нахож-дения параметраt:
в уравнение гиперболоида, получим
уравнение для нахож-дения параметраt:
![]() .
Его корни:
.
Его корни:
![]() .
Это означает, что имеются две точки
пересечения прямой с гиперболоидом:
.
Это означает, что имеются две точки
пересечения прямой с гиперболоидом:
![]() и
и![]() .
.
Какие еще могут быть варианты взаимного расположения прямой с однополостным гиперболоидом?
