
- •Аналитическая геометрия Лекция № 7. Тема 1 : Линии на плоскости и их уравнения
- •1.1. Линии и их уравнения в декартовой системе координат
- •1.2. Параметрические уравнения линий
- •1.3. Уравнение линии в полярной системе координат
- •1.4. Преобразование системы координат.
- •Лекция № 8. Тема 2 : Прямая линия на плоскости
- •2.1. Уравнения прямой линии
- •2.2. Угол между двумя прямыми
- •2.3. Взаимное расположение двух прямых
- •2.4. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой, проходящей через точку с заданным угловым коэффициентом
- •2.6. Расстояние от точки до прямой
- •Лекция № 9. Тема 3 : Линии второго порядка
- •3.1. Эллипс
- •3.2. Гипербола
- •10.3. Парабола
- •10.4. Классификация линий второго порядка
- •Лекция № 10. Тема 4 : Плоскость
- •4.1. Уравнение плоскости. Построение плоскости
- •4.2. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору
- •4.3. Уравнение плоскости, проходящей через три заданные точки
- •4.4. Угол между двумя плоскостями
- •4.5. Расстояние от точки до плоскости
- •Тема 5 : Прямая в пространстве
- •5.1. Уравнения прямой
- •Лекция № 11.
- •5.2. Уравнение прямой, проходящей через две точки
- •5.3. Угол между двумя прямыми
- •5.4. Расстояние от точки до прямой
- •5.5. Угол между прямой и плоскостью
- •5.6. Пересечение прямой с плоскостью
- •Лекция № 12. Тема 6 : Поверхности
- •6.1. Уравнение поверхности
- •6.2. Поверхности второго порядка
Лекция № 11.
5.2. Уравнение прямой, проходящей через две точки
Пусть требуется
составить уравнение прямой, проходящей
через две точки
![]() и
и![]() .
Возьмём в качестве направляющего вектора
.
Возьмём в качестве направляющего вектора![]() ,
а за начальную точку любую из точек
М1
и М2,
например, М1.
Тогда
уравнения
искомой прямой примут
вид
,
а за начальную точку любую из точек
М1
и М2,
например, М1.
Тогда
уравнения
искомой прямой примут
вид
![]() (1)
(1)
5.3. Угол между двумя прямыми
Очевидно, что углом
между двумя прямыми можно считать угол
между их направляющими векторами
![]() и
и![]() .
Тогда
.
Тогда
 (2)
(2)
Если прямые параллельны, то их направляющие векторы коллинеарны и условие параллельности принимает вид
![]()
Если прямые
перпендикулярны, то перпендикулярны
их направляющие векторы и условие
перпендикулярности
![]() из формулы
(2) примет вид
из формулы
(2) примет вид
![]()
Пример 1.
Две прямые
![]() и
и![]() проходят через начало координат. При
этом точки
проходят через начало координат. При
этом точки![]() .
При каком значении пара-метрар
они перпендикулярны?
.
При каком значении пара-метрар
они перпендикулярны?
В качестве первой
точки (см. формулу (1)) возьмём начало
координат
![]() ,
тогда направляющие векторы будут равны
,
тогда направляющие векторы будут равны
![]()
![]() , и
из условия перпендикулярности получаем
, и
из условия перпендикулярности получаем
![]()
5.4. Расстояние от точки до прямой
Пусть требуется
найти расстояние от точки
![]() до прямой l,
заданной каноническими уравнениями
до прямой l,
заданной каноническими уравнениями
![]()

Построим вектор
![]() .
z
M1
.
z
M1
Расстояние d от точки M1 до
Прямой l равно высоте параллело- M0 d
грамма, построенного
на векторах
![]() у
у
![]() и
и
![]() .
.
Так как площадь параллелограмма х l
![]() или
или
![]() ,
,
то получим
 (3)
(3)
Пример 2.
Найти
расстояние от точки
![]() до прямой
до прямой
![]()
Здесь
![]() И тогда имеем
И тогда имеем

5.5. Угол между прямой и плоскостью
Пусть плоскость P и прямая l заданы соответственно уравнениями:
![]()
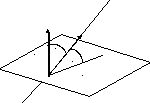
Здесь
![]()
нормальный вектор
l
нормальный вектор
l
плоскости P,
![]()
направляющий
направляющий
![]()
вектор прямой l, а угол между прямой
и плоскостью. l1
Если l1 проекция прямой l на P
плоскость P,
то
![]() и тогда
и тогда

Окончательно,
считая
![]() ,
получаем
,
получаем
 (4)
(4)
Если прямая и
плоскость перпендикулярны, то векторы
![]() и
и![]() коллинеарны,
и тогда условие перпендикулярности
примет вид
коллинеарны,
и тогда условие перпендикулярности
примет вид
![]()
Если они параллельны, то эти векторы перпендикулярны, и условие параллельности примет вид
![]()
5.6. Пересечение прямой с плоскостью
Пусть требуется
найти точку пересечения прямой
 с плоскостью
с плоскостью![]() .
.
Подставив параметрические уравнения прямой в уравнение плоскости, получим уравнение
![]()
Исключая параметр t, получим
![]() (5)
(5)
Здесь возможны три случая:
1.
![]() Тогда по формуле (5) вычисляем значение
пара-метраt
и из уравнений прямой определяем
координаты точки пересе-чения.
Тогда по формуле (5) вычисляем значение
пара-метраt
и из уравнений прямой определяем
координаты точки пересе-чения.
2.
![]() ,
а
,
а![]() .
В этом случае прямая параллельна
плоскости.
.
В этом случае прямая параллельна
плоскости.
3.
![]() и
и![]() .
Тогда прямая принадлежит плоскости.
.
Тогда прямая принадлежит плоскости.
Пример 3.
Определить взаимное расположение
прямой, проходящей через две точки
![]() и
и![]() ,
с плоскостью
,
с плоскостью![]()
Составим по формуле
(1) уравнения прямой проходящей через
эти точки:
![]()
Определим угол между этой прямой и плоскостью по формуле (4):
![]()
Из этого следует,
что прямая параллельна плоскости.
Проверим принадлежит ли она плоскости?
Подставим координаты точки
![]() в уравнение
плоскости:
в уравнение
плоскости:
![]()
откуда следует, что данная прямая принадлежит плоскости.
П ример
4. Составить
уравнение плоскости, проходящей через
прямую
ример
4. Составить
уравнение плоскости, проходящей через
прямую
 и точку
и точку![]() .Р
.Р
Из условия
компланарности векторов М
![]() М0
М0
![]() и
и
![]() имеемl
М1
имеемl
М1

Раскрывая
определитель, получим искомое уравнение
плоскости Р
![]()
