
- •Аналитическая геометрия Лекция № 7. Тема 1 : Линии на плоскости и их уравнения
- •1.1. Линии и их уравнения в декартовой системе координат
- •1.2. Параметрические уравнения линий
- •1.3. Уравнение линии в полярной системе координат
- •1.4. Преобразование системы координат.
- •Лекция № 8. Тема 2 : Прямая линия на плоскости
- •2.1. Уравнения прямой линии
- •2.2. Угол между двумя прямыми
- •2.3. Взаимное расположение двух прямых
- •2.4. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой, проходящей через точку с заданным угловым коэффициентом
- •2.6. Расстояние от точки до прямой
- •Лекция № 9. Тема 3 : Линии второго порядка
- •3.1. Эллипс
- •3.2. Гипербола
- •10.3. Парабола
- •10.4. Классификация линий второго порядка
- •Лекция № 10. Тема 4 : Плоскость
- •4.1. Уравнение плоскости. Построение плоскости
- •4.2. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору
- •4.3. Уравнение плоскости, проходящей через три заданные точки
- •4.4. Угол между двумя плоскостями
- •4.5. Расстояние от точки до плоскости
- •Тема 5 : Прямая в пространстве
- •5.1. Уравнения прямой
- •Лекция № 11.
- •5.2. Уравнение прямой, проходящей через две точки
- •5.3. Угол между двумя прямыми
- •5.4. Расстояние от точки до прямой
- •5.5. Угол между прямой и плоскостью
- •5.6. Пересечение прямой с плоскостью
- •Лекция № 12. Тема 6 : Поверхности
- •6.1. Уравнение поверхности
- •6.2. Поверхности второго порядка
3.1. Эллипс
Эллипс определяется уравнением
![]() (2)
(2)
Т.е. в уравнении
(1) нужно положить
![]()
Коэффициенты а и b называются соответственно большой и малой полуосями, а уравнение (2) – каноническим уравнением эллипса.
Положим
![]() и отметим на осиОх
точки
и отметим на осиОх
точки
![]()
![]() называемыефокусами
эллипса. Тогда эллипс можно определить
как
называемыефокусами
эллипса. Тогда эллипс можно определить
как
геометрическое место точек, сумма расстояний от которых до фокусов есть величина постоянная, равная 2а.
 у
у
b
M K


-а F1 O F2 a x
-b
Покажем это. Пусть
точка
![]()
текущая точка эллипса. В этом случае
получаем
текущая точка эллипса. В этом случае
получаем
![]() Тогда должно выполняться равенство
Тогда должно выполняться равенство
![]() (3)
(3)
Выражение (3) представим в виде
![]()
и возведём в квадрат обе части выражения
![]()
Отсюда получаем
![]()
Еще раз возведём
это выражение в квадрат и воспользуемся
соотно-шением
![]() ,
тогда
,
тогда
![]() (4)
(4)
Разделив обе части
выражения (4) на
![]() ,
окончательно получаем каноническое
уравнение эллипса
,
окончательно получаем каноническое
уравнение эллипса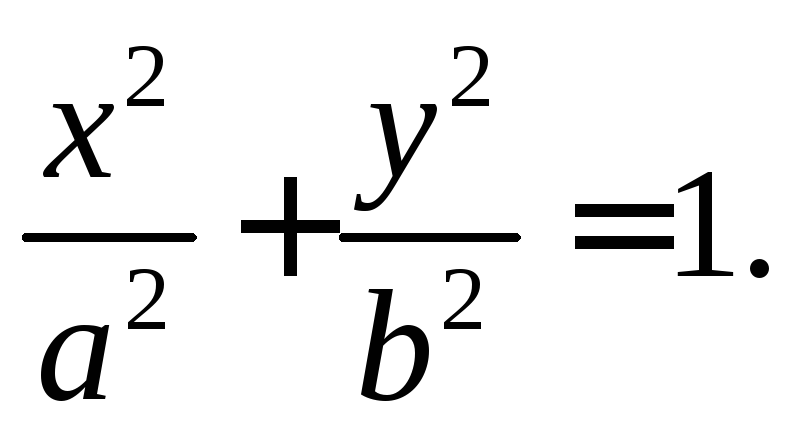
Исследуем уравнение
(2). Если в уравнении заменить
![]() ,
то уравнение (2) не изменится. Это означает,
что эллипс симметричен относительно
координатных осей. Поэтому рассмотрим
подробно часть эллипса, находящуюся в
первой четверти. Она определяется
уравнением
,
то уравнение (2) не изменится. Это означает,
что эллипс симметричен относительно
координатных осей. Поэтому рассмотрим
подробно часть эллипса, находящуюся в
первой четверти. Она определяется
уравнением![]() Очевидно, что эллипс проходит через
точки
Очевидно, что эллипс проходит через
точки![]() .
Выполнив схематическое построение в
первой четверти, симметрично отобразим
его график во все четверти. Таким образом,
эллипс является непрерывной замкнутой
кривой. Точки
.
Выполнив схематическое построение в
первой четверти, симметрично отобразим
его график во все четверти. Таким образом,
эллипс является непрерывной замкнутой
кривой. Точки![]() называютсявершинами
эллипса.
называютсявершинами
эллипса.
Отношение
![]() называетсяэксцентриситетом
эллипса. Для эллипса
называетсяэксцентриситетом
эллипса. Для эллипса
![]() .
.
Прямые
![]() называютсядиректрисами
эллипса.
называютсядиректрисами
эллипса.
Справедливо следующее свойство директрис:
Отношение расстояний
от фокуса и директрисы для точек эллипса
есть величина постоянная, равная
эксцентриситету, т.е.

Доказывается аналогично, как и равенство (3).
Замечание 1.
Окружность
![]() является частным случаем эллипса. Для
неё
является частным случаем эллипса. Для
неё![]()
3.2. Гипербола
Каноническое уравнение гиперболы имеет вид
![]()
т.е. в уравнении
(1) нужно положить
![]()
Коэффициенты а и b называются соответственно вещественной и мнимой полуосями.
Положив
![]() ,
отметим на осиОх
точки
,
отметим на осиОх
точки
![]() на-зываемыефокусами
гиперболы. Тогда гиперболу можно
определить как
на-зываемыефокусами
гиперболы. Тогда гиперболу можно
определить как
геометрическое место точек, разность расстояний от которых до фокусов по абсолютной величине равна 2а, т.е.
![]()

 у
у

К М
F1 -а О а F2 х


Доказывается
аналогично, как и для эллипса. По виду
уравнения гиперболы так же заключаем,
что её график симметричен относительно
осей системы координат. Часть гиперболы,
лежащая в первой четверти, имеет уравнение
![]() Из этого уравнения видно, что при
достаточно большихх
гипербола близка к прямой
Из этого уравнения видно, что при
достаточно большихх
гипербола близка к прямой
![]() .
После схематичного построения в
первой четверти симметрично отобра-жаем
график во все четверти.
.
После схематичного построения в
первой четверти симметрично отобра-жаем
график во все четверти.
Точки
![]() называютсявершинами
гиперболы. Прямые
называютсявершинами
гиперболы. Прямые
![]() называютсяасимптотами
– это прямые, к которым стремятся
ветви гиперболы, не пересекая их.
называютсяасимптотами
– это прямые, к которым стремятся
ветви гиперболы, не пересекая их.
Отношение
![]() называетсяэксцентриситетом
гиперболы. Для гиперболы
называетсяэксцентриситетом
гиперболы. Для гиперболы
![]() .
.
Прямые
![]() называютсядиректрисами
гиперболы. Для директрис гиперболы
имеет место свойство, аналогичное, как
и для директрис эллипса.
называютсядиректрисами
гиперболы. Для директрис гиперболы
имеет место свойство, аналогичное, как
и для директрис эллипса.
Пример.
Найти уравнение эллипса, вершины которого
находятся в фокусах, а фокусы в вершинах
гиперболы
![]() .
.
По условию
![]() а
а
![]()
Окончательно
получаем
![]()
