
- •Аналитическая геометрия Лекция № 7. Тема 1 : Линии на плоскости и их уравнения
- •1.1. Линии и их уравнения в декартовой системе координат
- •1.2. Параметрические уравнения линий
- •1.3. Уравнение линии в полярной системе координат
- •1.4. Преобразование системы координат.
- •Лекция № 8. Тема 2 : Прямая линия на плоскости
- •2.1. Уравнения прямой линии
- •2.2. Угол между двумя прямыми
- •2.3. Взаимное расположение двух прямых
- •2.4. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой, проходящей через точку с заданным угловым коэффициентом
- •2.6. Расстояние от точки до прямой
- •Лекция № 9. Тема 3 : Линии второго порядка
- •3.1. Эллипс
- •3.2. Гипербола
- •10.3. Парабола
- •10.4. Классификация линий второго порядка
- •Лекция № 10. Тема 4 : Плоскость
- •4.1. Уравнение плоскости. Построение плоскости
- •4.2. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору
- •4.3. Уравнение плоскости, проходящей через три заданные точки
- •4.4. Угол между двумя плоскостями
- •4.5. Расстояние от точки до плоскости
- •Тема 5 : Прямая в пространстве
- •5.1. Уравнения прямой
- •Лекция № 11.
- •5.2. Уравнение прямой, проходящей через две точки
- •5.3. Угол между двумя прямыми
- •5.4. Расстояние от точки до прямой
- •5.5. Угол между прямой и плоскостью
- •5.6. Пересечение прямой с плоскостью
- •Лекция № 12. Тема 6 : Поверхности
- •6.1. Уравнение поверхности
- •6.2. Поверхности второго порядка
Аналитическая геометрия Лекция № 7. Тема 1 : Линии на плоскости и их уравнения
1.1. Линии и их уравнения в декартовой системе координат
В аналитической геометрии линии на плоскости рассматриваются как геометрическое место точек (г.м.т.), обладающих одинаковым свойством, общим для всех точек линии.
О пределение.
Уравнение линии
пределение.
Уравнение линии
![]() – это уравнение с двумя переменнымих
и у,
которому удовлетворяют координаты
любой точки линии и не удовлетворяют
координаты никакой другой точки, не
лежащей на данной линии.
– это уравнение с двумя переменнымих
и у,
которому удовлетворяют координаты
любой точки линии и не удовлетворяют
координаты никакой другой точки, не
лежащей на данной линии.
Верно и обратное, т.е. любое уравнение у
вида
![]() ,
вообще говоря, в декартовой
,
вообще говоря, в декартовой![]()
![]()
системе координат (ДСК) определяет линию
как г.м.т.,
координаты которых удовлетворяют
![]()
![]()
этому уравнению.
О
![]() х
х
Замечание 1.
Не всякое уравнение вида
![]() определяет линию. Например, для уравнения
определяет линию. Например, для уравнения![]() не существует точек, координаты, которых
удовлетворяли бы этому уравнению. Такие
случаи в дальнейшем рассматривать не
будем.
Это случай
так называемых мнимых линий.
не существует точек, координаты, которых
удовлетворяли бы этому уравнению. Такие
случаи в дальнейшем рассматривать не
будем.
Это случай
так называемых мнимых линий.
П ример
1. Составить
уравнение окружности радиуса R
с центром в точке
ример
1. Составить
уравнение окружности радиуса R
с центром в точке
![]() .
.
Для любой точки
![]() ,
лежащейу
М
,
лежащейу
М
на окружности, в силу определения R
окружности как
г.м.т., равноудаленных
![]()
от точки
![]() ,
получаем уравнениех
,
получаем уравнениех
![]() .
.
1.2. Параметрические уравнения линий
Существует ещё один способ задавать линию на плоскости при помощи уравнений, которые называются параметрическими:

Пример 1.
Линия задана параметрическими
уравнениями
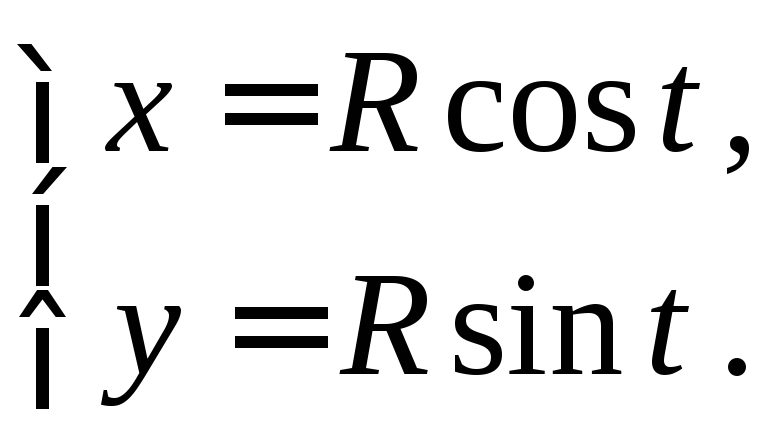
Требуется получить уравнение этой линии в ДСК.
Исключим параметр t. Для этого возведём обе части этих уравнений в квадрат и сложим
![]()

Пример 2. Линия задана параметрическими уравнениями
 а
а
Требуется получить уравнение
этой линии в ДСК. -а а
Поступим аналогично, тогда получим
![]() -а
-а
Замечание 2. Следует отметить, что параметром t в механике явля-ется время.
1.3. Уравнение линии в полярной системе координат
ДСК является не единственным способом определять положение точки и, следовательно, задавать уравнение линии. На плоскости часто целесо-образно использовать так называемую полярную систему координат (ПСК).
П СК
будет определена, если задать точкуО
– полюс и луч ОР,
исхо-дящий из этой точки, который
называется полярной осью. Тогда положение
любой точки определяется двумя числами:
полярным радиусом
СК
будет определена, если задать точкуО
– полюс и луч ОР,
исхо-дящий из этой точки, который
называется полярной осью. Тогда положение
любой точки определяется двумя числами:
полярным радиусом
![]() и полярным углом
и полярным углом![]() – угол между
– угол между
полярной осью и
полярным радиусом.
![]()
Положительное
направление отсчета
![]()
полярного угла от полярной оси
считается против
часовой стрелки.
![]()
Для всех точек
плоскости
![]() ,О
Р
,О
Р
а для однозначности
полярного угла считается
![]() .
.
Е сли
начало ДСК совместить с
сли
начало ДСК совместить с
полюсом, а ось Ох направить по
полярной оси, то
легко убедиться у
![]()
в связи между
полярными и
![]()
декартовыми
координатами:
![]()
 О
х
Р
О
х
Р
Обратно,
 (1)
(1)
Если уравнение
линии в ДСК имеет вид
![]() ,
то в ПСК -
,
то в ПСК -![]() Тогда из этого уравнения можно получить
урав-нение в виде
Тогда из этого уравнения можно получить
урав-нение в виде![]()
Пример 3. Составить уравнение окружности в ПСК, если центр окружности находится в полюсе.
Используя формулы перехода (1) от ДСК к ПСК, получим
![]()
П ример
4. Составить
уравнение окружности,
ример
4. Составить
уравнение окружности,
если полюс на окружности, а полярная ось у
проходит через
диаметр.
![]()
Поступим аналогично
![]()
![]() О
2R
х
О
2R
х
![]() R
R
Данное уравнение можно получить и
из геометрических представлений (см. рис.).
П ример
5. Построить
график линии
ример
5. Построить
график линии
![]()
Перейдём к ПСК. Уравнение
примет вид
![]() О
О
![]()
График линии построим с а
учётом его симметрии и ОДЗ
функции:
![]()
Данная линия называется лемнискатой Бернулли.
