
- •Функции нескольких переменных
- •Тема 1 : Предел. Непрерывность. Частные производные
- •1.1. Определение функции нескольких переменных
- •1.2. Предел и непрерывность функции двух переменных
- •1.3. Частные производные функции двух переменных
- •1.4. Полный дифференциал функции двух переменных
- •1.5. Производная сложной функции
- •2.4. Производная по направлению
- •2.5. Градиент функции
- •Лекция № 34
- •2.6. Касательная и нормаль к поверхности
- •Тема 3* : Векторная функция скалярного аргумента
- •3.1. Векторная функция. Предел. Непрерывность
- •3.2. Производная векторной функции
Функции нескольких переменных
Тема 1 : Предел. Непрерывность. Частные производные
1.1. Определение функции нескольких переменных
Остановимся, в основном, на случае функции двух переменных. Определения и полученные результаты легко распространить и на случай большего числа переменных.
Рассмотрим
плоскость Оху
множество всех точек
![]() .
.
Определение 1.
Множество всех точек
![]() ,
координаты которых удовлетворяют
неравенству
,
координаты которых удовлетворяют
неравенству![]() ,
называется
,
называется![]() окрест-ностью
точки
окрест-ностью
точки
![]() и обозначается
и обозначается![]() .
.
Определение 2. Областью D называется множество точек, обладающих свойствами:
1. Любая точка
![]() принадлежит ей и вместе с некоторой
принадлежит ей и вместе с некоторой![]() - окрестностью (свойство
открытости);
- окрестностью (свойство
открытости);
2. Любые точки
![]() и
и![]() можно соединить непрерывной линией,
целиком принадлежащейD
(свойство связности).
можно соединить непрерывной линией,
целиком принадлежащейD
(свойство связности).
Л иния,
ограничивающая данную область, называетсяграницей.
Если к области отнести и
точки границы,
то такая область называется замкнутой.
иния,
ограничивающая данную область, называетсяграницей.
Если к области отнести и
точки границы,
то такая область называется замкнутой.
D
М1 М2
![]()
Определение 3.
Если каждой паре
![]() значений двух независимых переменных
из некоторой областиD
соответствует по некоторому правилу
или закону определённое значение
величины z,
то z
называется функцией двух переменных
в области D,
и
пишут
значений двух независимых переменных
из некоторой областиD
соответствует по некоторому правилу
или закону определённое значение
величины z,
то z
называется функцией двух переменных
в области D,
и
пишут
![]() .
.
Аналогично, как и для функции одной переменной определяется многозначная функция нескольких переменных.
Пример 1.
Закон Ома:
![]()
функция двух переменных.
функция двух переменных.
Пример 2.
Работа постоянной силы на прямолинейном
перемещении:
![]()
функция трёх переменных.
функция трёх переменных.
Определение 4.
Множество значений
![]() ,
при которых определена
,
при которых определена![]() ,
называетсяобластью
определения
функции.
,
называетсяобластью
определения
функции.
Пример 3. Найти область определения функций:
1.
![]() ,
т.е. областью определения данной функции
является круг
,
т.е. областью определения данной функции
является круг![]() .
.
2.
![]() ,
т.е. область определения
первая и третья координатные четверти
без координатных осей.
,
т.е. область определения
первая и третья координатные четверти
без координатных осей.
Геометрически
функцию двух переменных можно представить
как поверхность, уравнение которой
![]() .
Например, уравнение функции
.
Например, уравнение функции![]() геометрически представляет параболоид.
геометрически представляет параболоид.
1.2. Предел и непрерывность функции двух переменных
Точка
![]() стремится к точке
стремится к точке![]() ,
если расстояние между этими точками
стремится к нулю, т.е.
,
если расстояние между этими точками
стремится к нулю, т.е.![]() .
Это очевидно эквивалентно:
.
Это очевидно эквивалентно:
![]() .
.
Определение 5.
Число А
называется пределом функции
![]() при стремлении точки
при стремлении точки![]() ,
если
,
если![]() ,
для всех точек из которой выполняется
неравенство
,
для всех точек из которой выполняется
неравенство![]() ,
и пишут
,
и пишут
![]() или
или
![]() .
.
Аналогично
устанавливается понятие о бесконечном
пределе функции. В случае, когда
![]() или
или![]() ,
неравенство
,
неравенство![]() заменяется неравенствами вида:
заменяется неравенствами вида:
![]() или
или![]() соответственно, гдеМ
произвольное положительное число, и
пишут
соответственно, гдеМ
произвольное положительное число, и
пишут
![]() или
или
![]() .
.
Определение 6.
Функция
![]() имеет пределом числоА
при
имеет пределом числоА
при
![]() и
и![]() если
если![]() ,
что
,
что![]() при
при![]() и пишут
и пишут
![]() .
.
Определение 7. Функция называется непрерывной в точке М0, если имеет место равенство
![]() .
.
Если в некоторой точке условие непрерывности не выполняется, такая точка называется точкой разрыва.
Пример 4.
Исследовать на непрерывность функцию
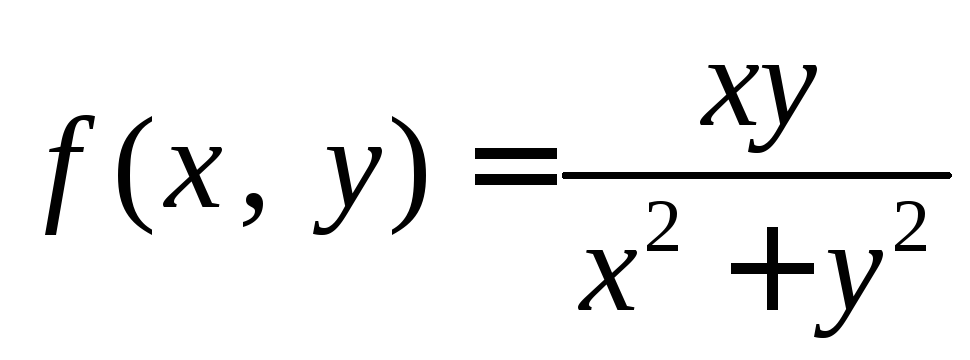 в точке
в точке![]()
Рассмотрим значения
функции вдоль прямых
![]() при
при
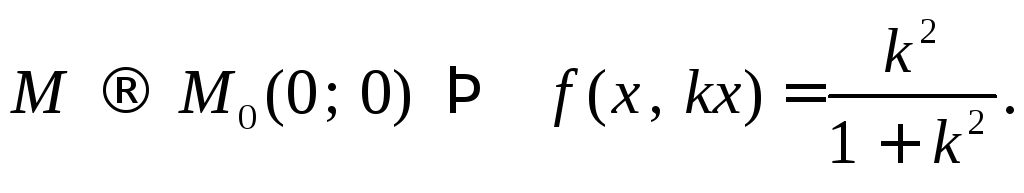 .
.
Таким образом,
функция принимает разные значения в
зависимости от значения k.
Точка
![]() является точкой разрыва.
является точкой разрыва.
Замечание. Свойства непрерывной функции двух переменных аналогичны соответствующим свойствам функции одной переменной.
