
Для студентов ЭКИ-1 / RGR-2
.doc
3.9 ![]() . 3.10
. 3.10 ![]() .
.
3.11 ![]() . 3.12
. 3.12 ![]() .
.
3.13 ![]() . 3.14
. 3.14 ![]() .
.
3.15 ![]() . 3.16
. 3.16 ![]() .
.
3.17 ![]() . 3.18
. 3.18 ![]() .
.
3.19 ![]() . 3.20
. 3.20 ![]() .
.
3.21 ![]() . 3.22
. 3.22 ![]() .
.
3.23 ![]() . 3.24
. 3.24 ![]() .
.
4. Вычислить пределы функций:
4.1 a)
![]() ; б)
; б)
![]() ;
;
в)
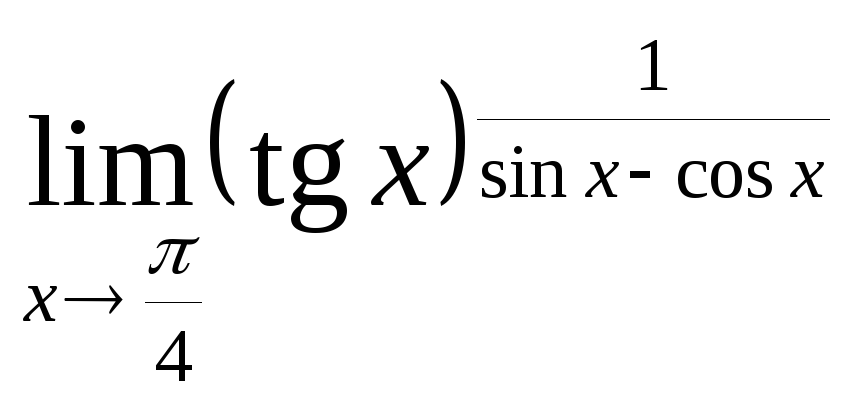 ; г)
; г)
![]() .
.
4.2 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.3 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.4 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.5 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.6 a)
![]() ; б)
; б)
 ;
;
в)
![]() ; г)
; г)
![]() .
.
4.7 a)
![]() ; б)
; б)
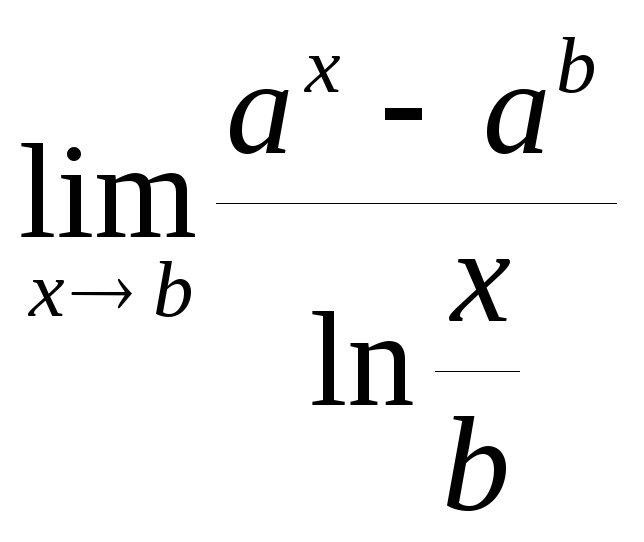 ;
;
в)
![]() ; г)
; г)
![]() .
.
4.8 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.9 a)
![]() ; б)
; б)
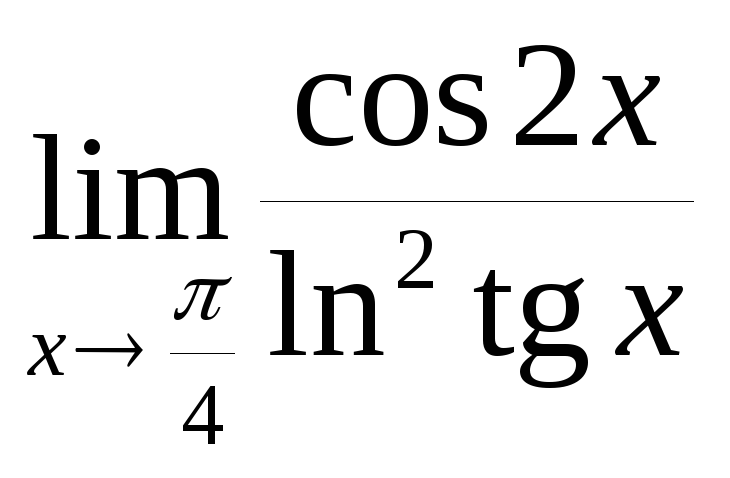 ;
;
в)
![]() ; г)
; г)
![]() .
.
4.10 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.11 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.12 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.13 a)
![]() ; б)
; б)
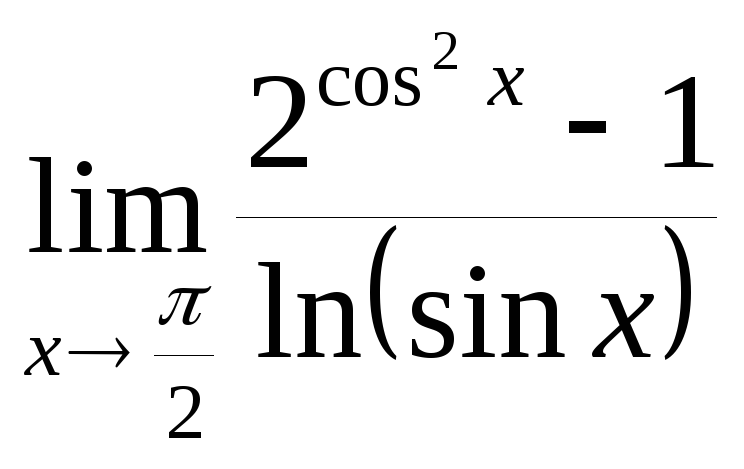 ;
;
в)
![]() ; г)
; г)
![]() .
.
4.14 a)
![]() ; б)
; б)
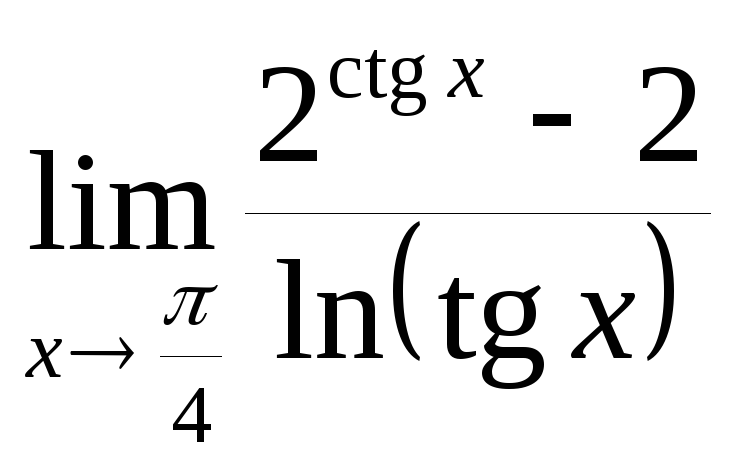 ;
;
в)
![]() ; г)
; г)
![]() .
.
4.15 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.16 a)
![]() ; б)
; б)
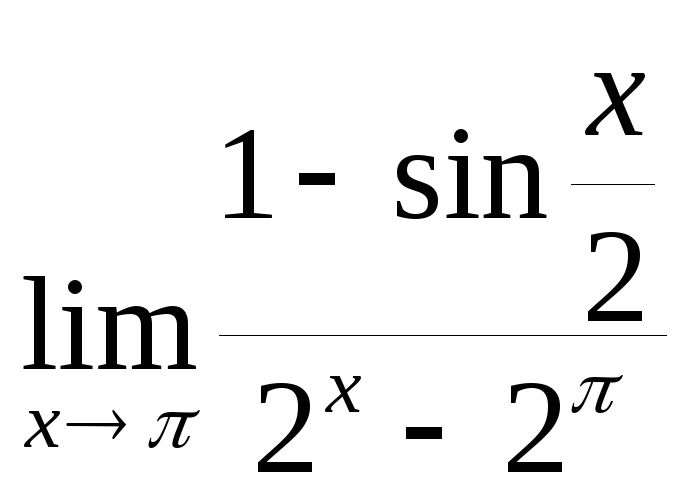 ;
;
в)
![]() ; г)
; г)
![]() .
.
4.17 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.18 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.19 a)
![]() ; б)
; б)
 ;
;
в)
![]() ; г)
; г)
![]() .
.
4.20 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
 .
.
4.21 a)
![]() ; б)
; б)
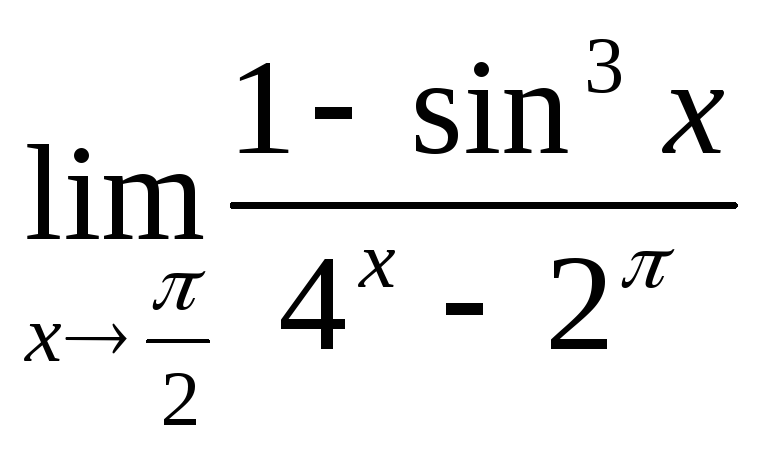 ;
;
в)
![]() ; г)
; г)
 .
.
4.22 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4.23 a)
![]() ; ` б)
; ` б)
![]() ;
;
в)
![]() ; г)
; г)
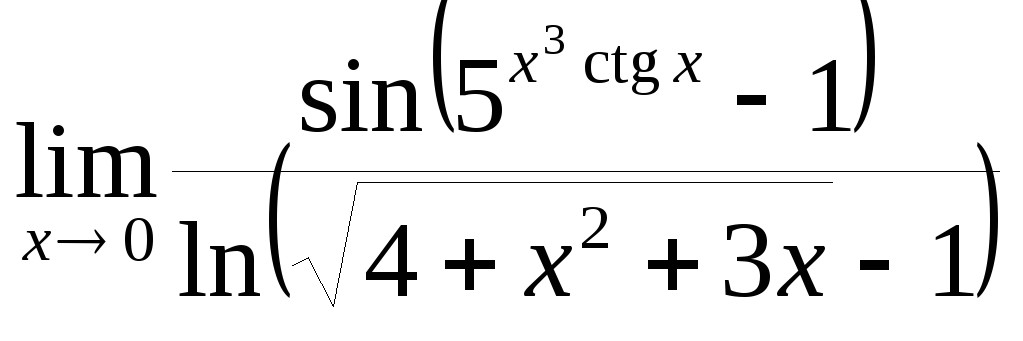 .
.
4.24 a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
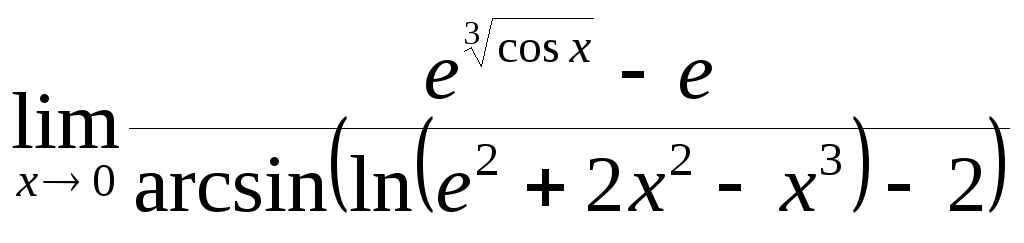 .
.
5. Выяснить
зависимость предела функции или
последовательности от параметра (
![]() – целая часть числа
– целая часть числа
![]() ):
):
5.1 ![]() . 5.2
. 5.2 ![]() .
.
5.3 ![]() . 5.4
. 5.4 ![]() .
.
5.5 ![]() . 5.6
. 5.6 ![]() .
.
5.7 ![]() . 5.8
. 5.8 ![]() .
.
5.9 ![]() . 5.10
. 5.10 ![]() .
.
5.11 ![]() . 5.12
. 5.12 ![]() .
.
5.13 ![]() . 5.14
. 5.14 ![]() .
.
5.15 ![]() . 5.16
. 5.16 ![]() .
.
5.17 ![]() . 5.18
. 5.18 ![]() .
.
5.19 ![]() . 5.20
. 5.20 ![]() .
.
5.21 ![]() . 5.22
. 5.22 ![]() .
.
5.23 ![]() . 5.24
. 5.24 ![]() .
.
6. Исследовать функцию на непрерывность. В пункте а) построить график, в пунктах б) и в) показать поведение функции в окрестностях точек разрыва:
6.1 а)
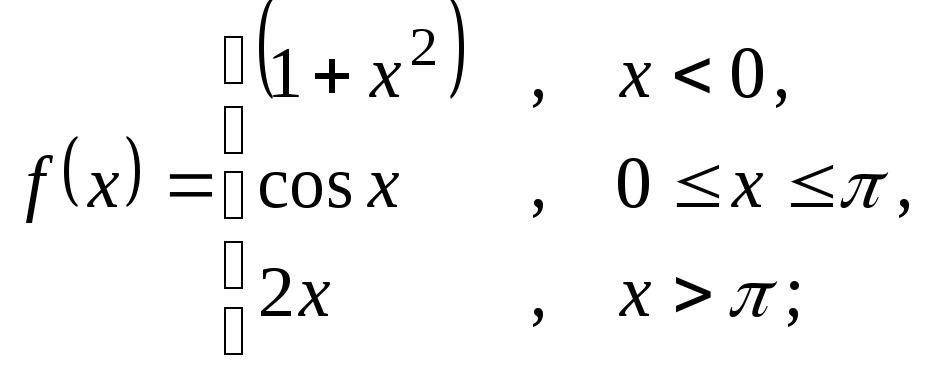
б)
![]() ; в)
; в)
![]() .
.
6.2 а)
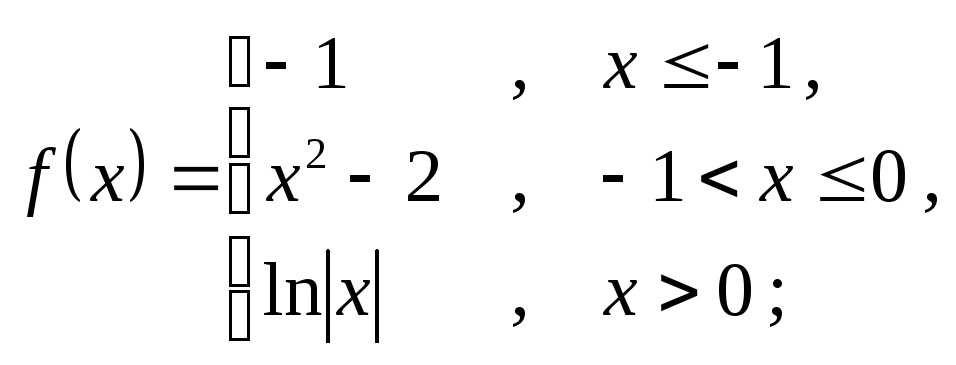
б)
![]() ; в)
; в)
 .
.
6.3 а)

б)
![]() ; в)
; в)
![]() .
.
6.4 а)

б)
![]() ; в)
; в)
![]() .
.
6.5 а)

б)
![]() ; в)
; в)
![]() .
.
6.6 а)

б)
![]() ; в)
; в)
![]() .
.
6.7 а)
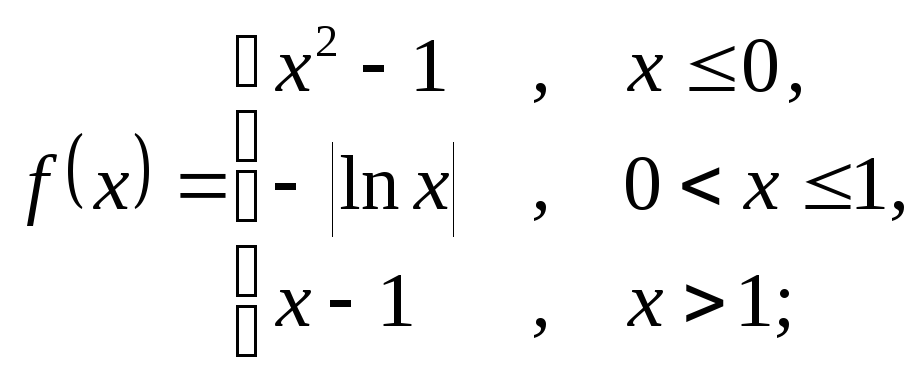
б)
![]() ; в)
; в)
![]() .
.
6.8 а)
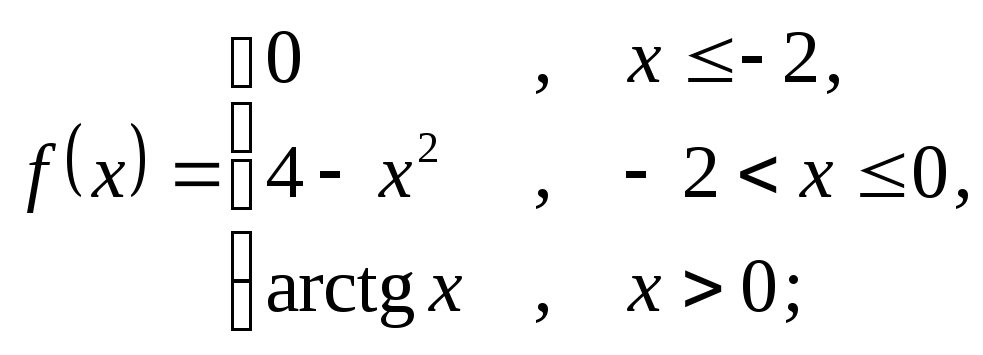
б)
![]() ; в)
; в)
![]() .
.
6.9 а)
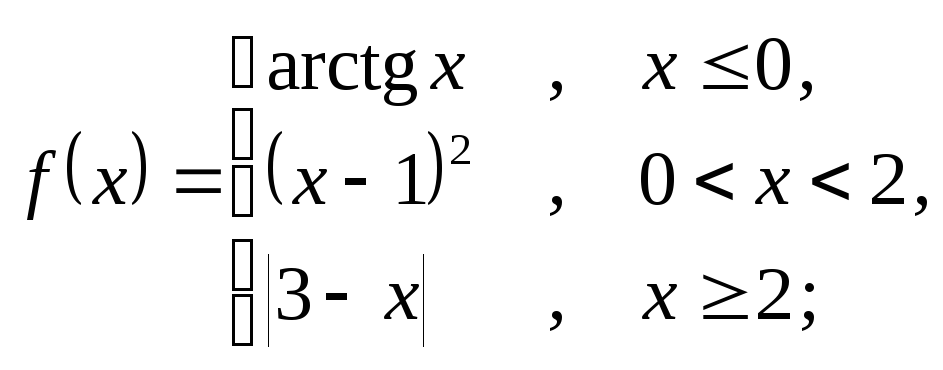
б)
![]() ; в)
; в)
![]() .
.
6.10 а)

б)
![]() ; в)
; в)
![]() .
.
6.11 а)

б)
![]() ; в)
; в)
![]() .
.
6.12 а)
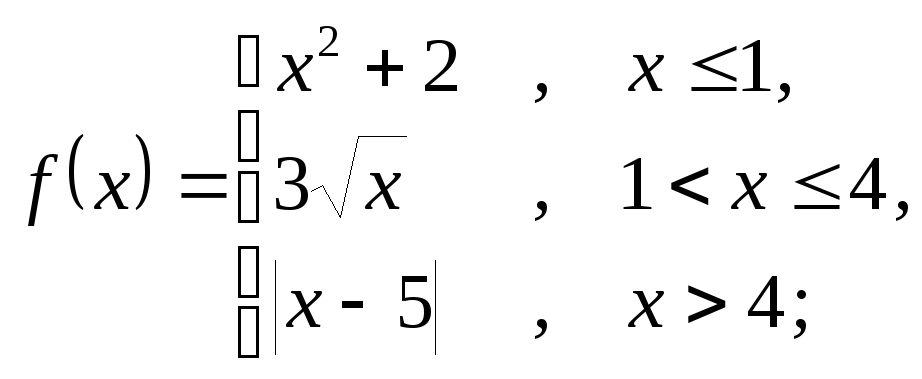
б)
![]() ; в)
; в)
![]() .
.
6.13 а)
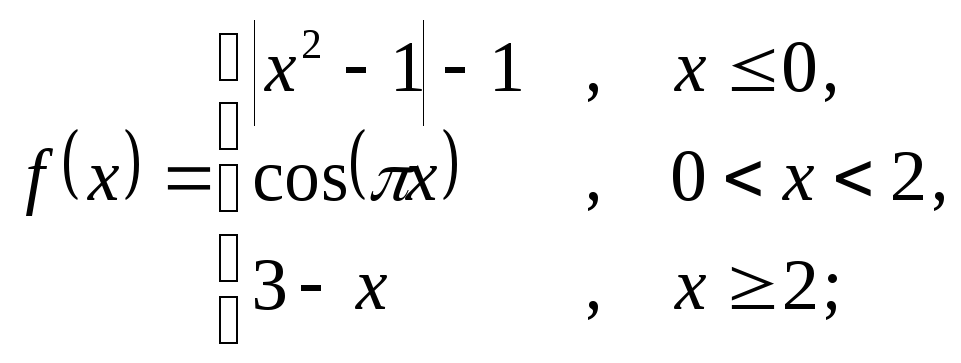
б)
![]() ; в)
; в)
![]() .
.
6.14 а)
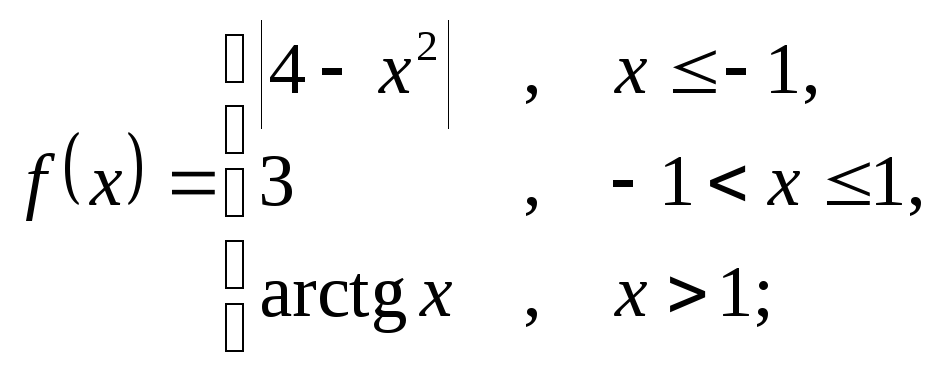
б)
![]() ; в)
; в)
![]() .
.
6.15 а)
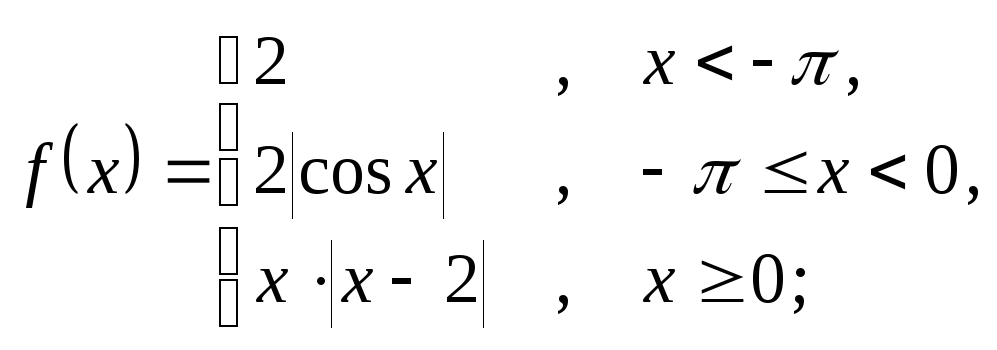
б)
![]() ; в)
; в)
![]() .
.
6.16 а)
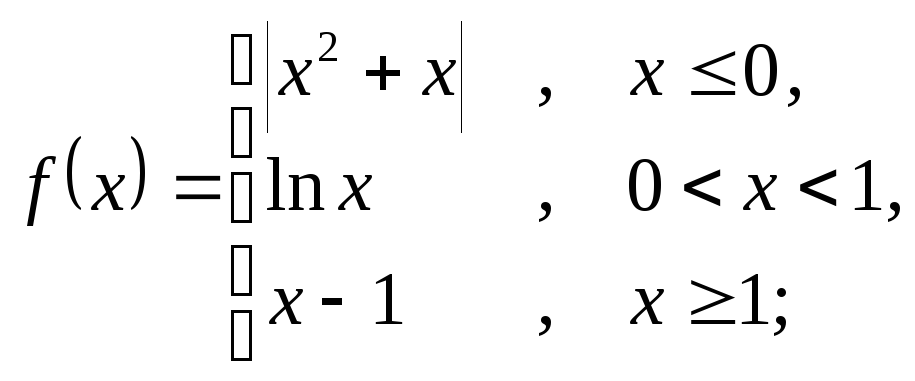
б)
![]() ; в)
; в)
![]() .
.
6.17 а)

б)
![]() ; в)
; в)
![]() .
.
6.18 а)

б)
![]() ; в)
; в)
![]() .
.
6.19 а)
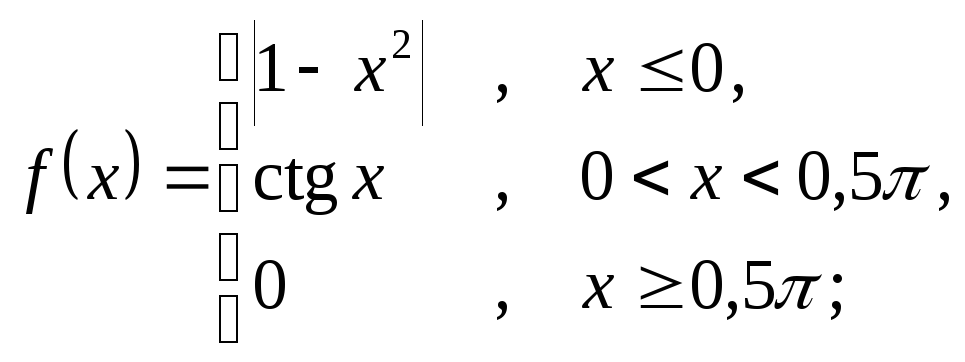
б)
![]() ; в)
; в)
![]() .
.
6.20 а)
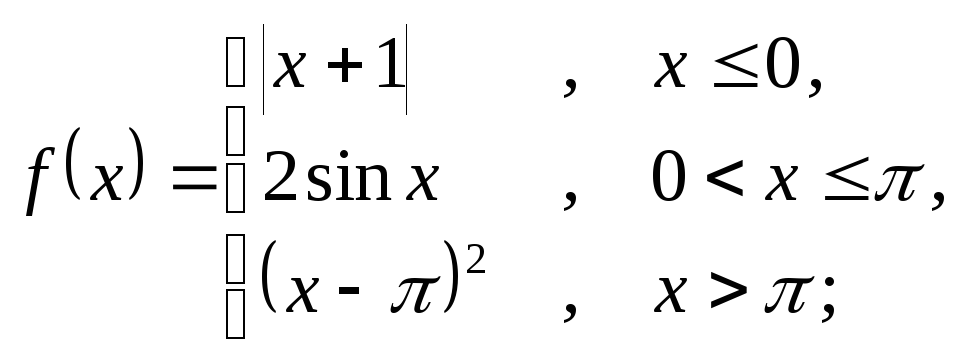
б)
![]() ; в)
; в)
![]() .
.
6.21 а)
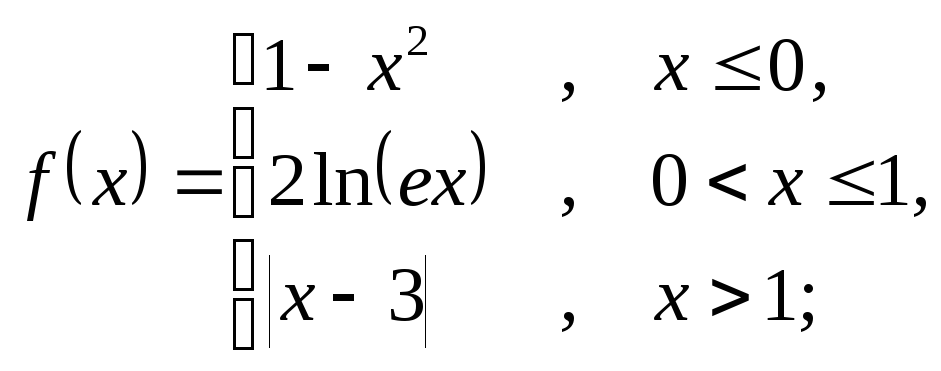
б)
![]() ; в)
; в)
![]() .
.
6.22 а)
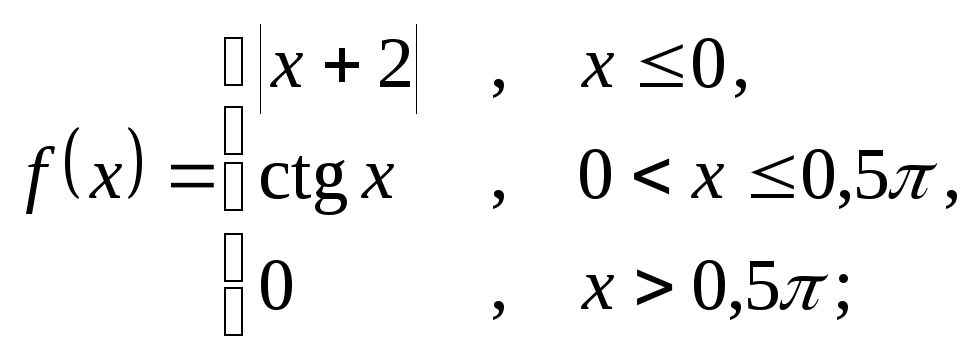
б)
![]() ; в)
; в)
![]() .
.
6.23 а)
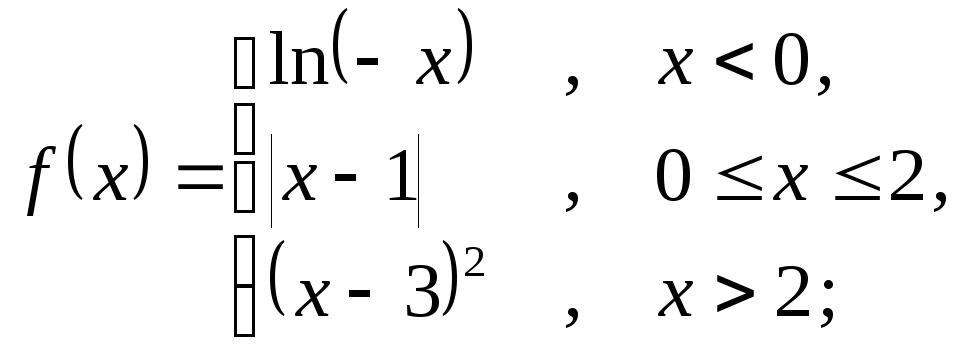
б)
![]() ; в)
; в)
![]() .
.
6.24 а)
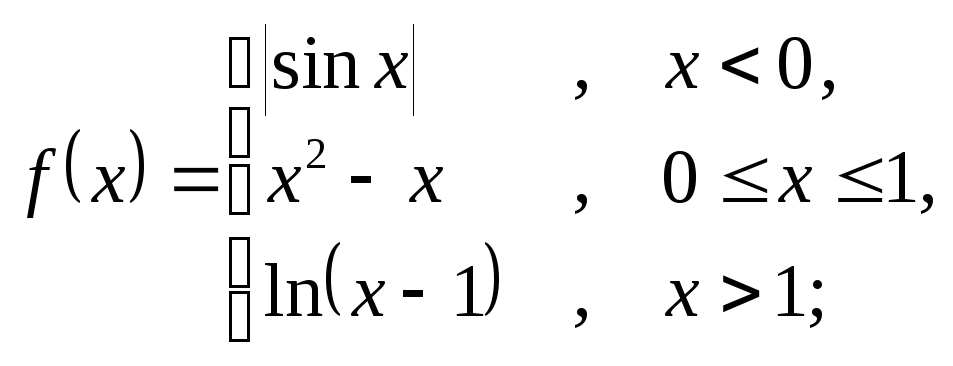
б)
![]() ; в)
; в)
![]() .
.
7. Построить график функции, указать точки разрыва:
7.1 ![]() . 7.2
. 7.2 ![]() .
.
7.3 ![]() . 7.4
. 7.4 ![]() .
.
7.5 ![]() . 7.6
. 7.6 ![]() .
.
7.7 ![]() . 7.8
. 7.8 ![]() .
.
7.9 ![]() . 7.10
. 7.10 ![]() .
.
7.11 ![]() . 7.12
. 7.12 ![]() .
.
7.13 ![]() . 7.14
. 7.14 ![]() .
.
7.15 ![]() . 7.16
. 7.16 ![]() .
.
7.17 ![]() . 7.18
. 7.18 ![]() .
.
7.19 ![]() . 7.20
. 7.20 ![]() .
.
7.21 ![]() . 7.22
. 7.22 ![]() .
.
7.23 ![]() . 7.24
. 7.24 ![]() .
.
8. Положить
![]() и вычислить производную функции.
Исследовать, при каких значениях
параметра
и вычислить производную функции.
Исследовать, при каких значениях
параметра
![]() функция: 1) непрерывна; 2) дифференцируема;
3) непрерывно-дифференцируема.
функция: 1) непрерывна; 2) дифференцируема;
3) непрерывно-дифференцируема.
8.1
![]()
 8.2
8.2
![]()

8.3
![]()
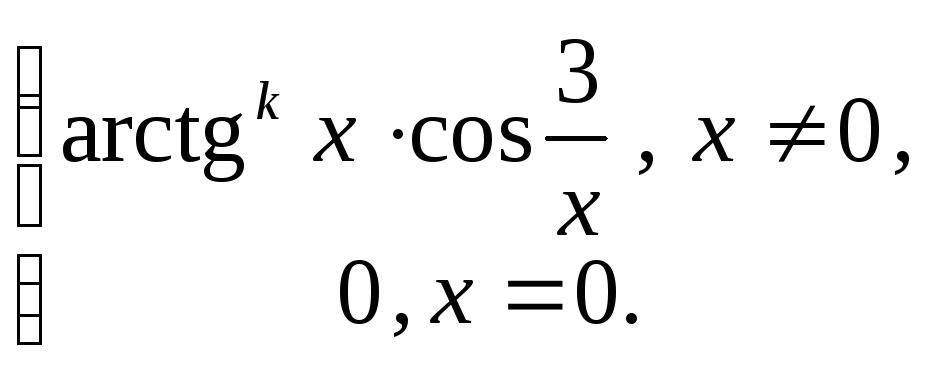 8.4
8.4
![]()

8.5
![]()
 8.6
8.6
![]()
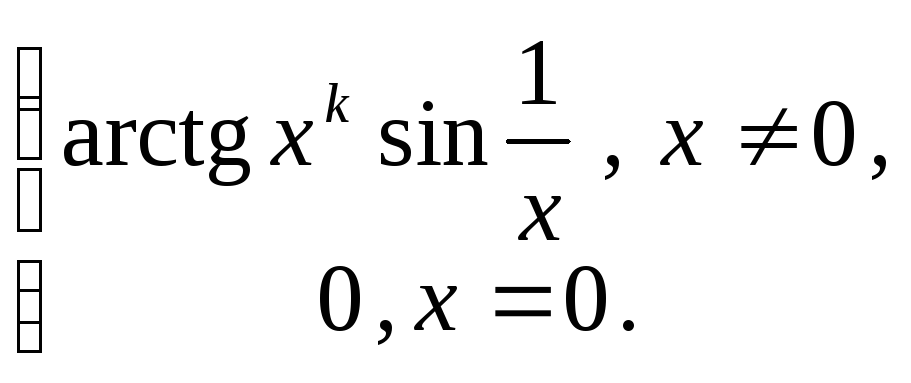
8.7
![]()
 8.8
8.8
![]()
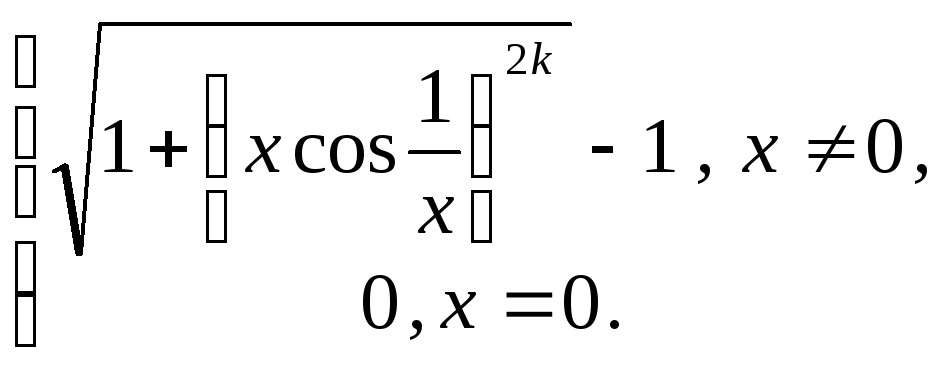
8.9
![]()
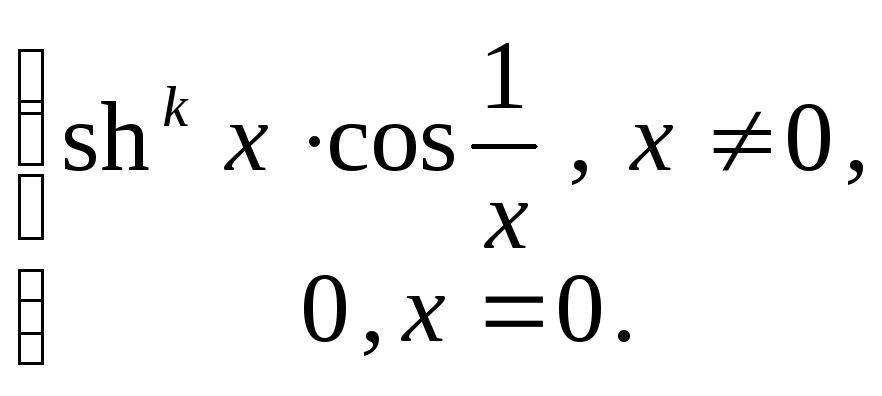 8.10
8.10
![]()
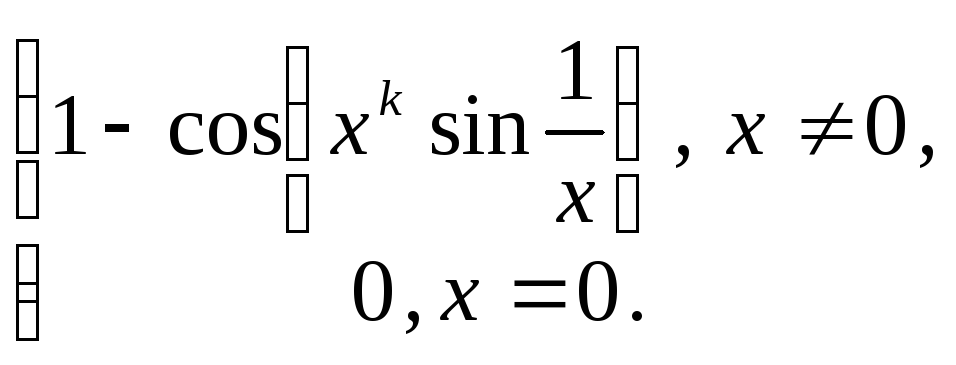
8.11
![]()
 8.12
8.12
![]()
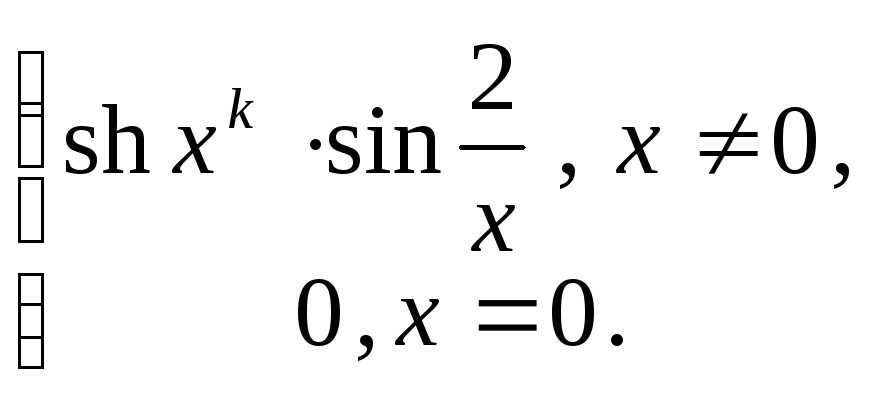
8.13
![]()
 8.14
8.14
![]()
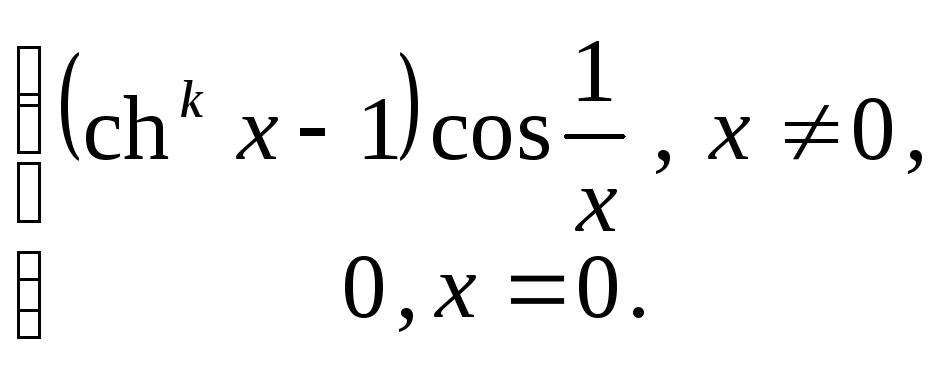
8.15
![]()
 8.16
8.16
![]()
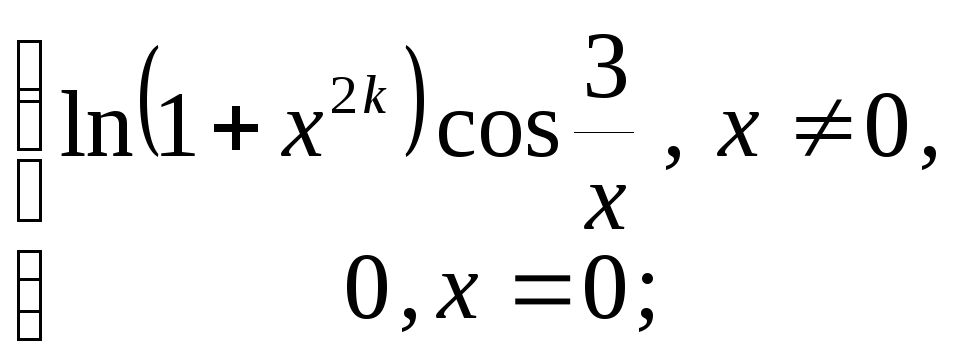
8.17
![]()
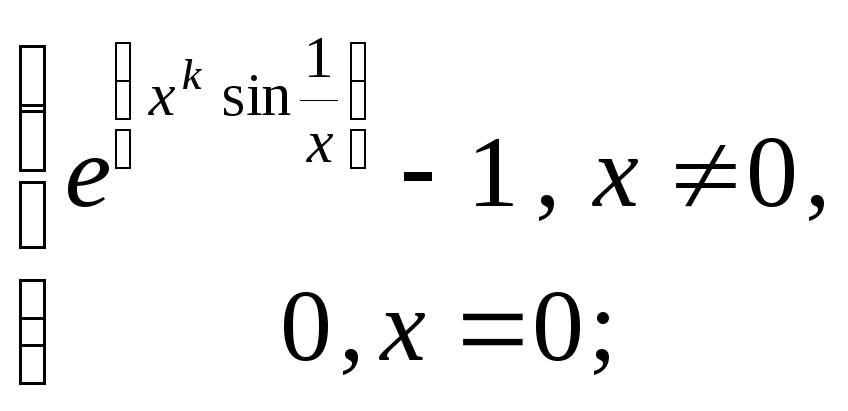 8.18
8.18
![]()

8.19
![]()
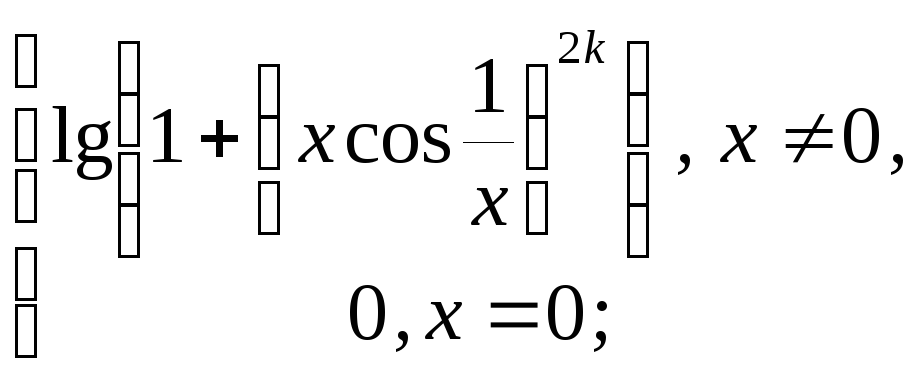 8.20
8.20
![]()

8.21
![]()
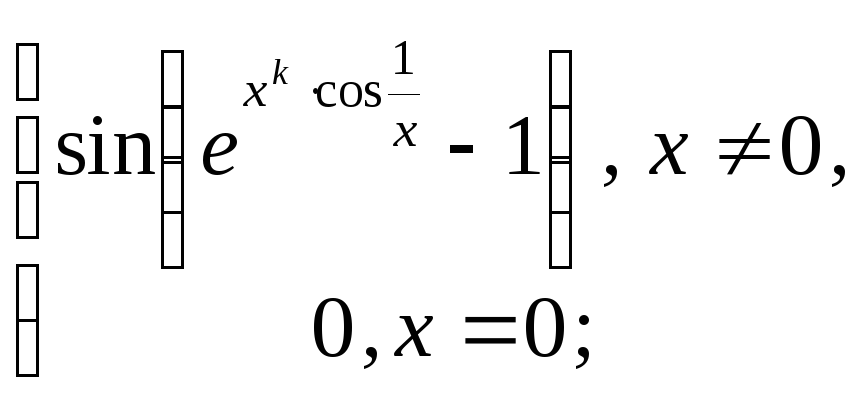 8.22
8.22
![]()
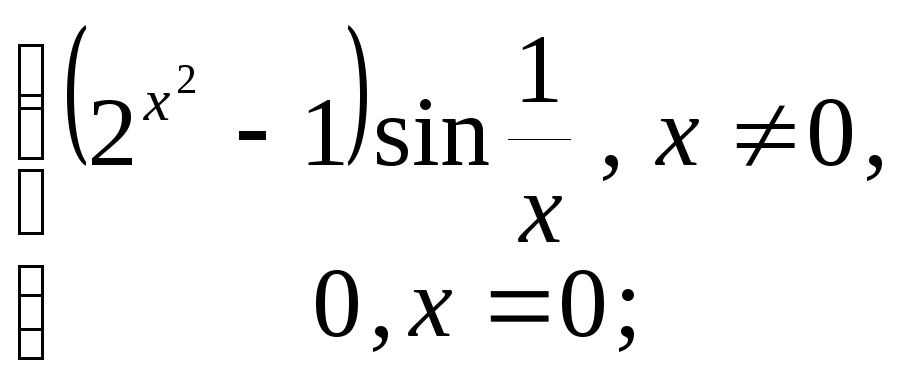
8.23
![]()
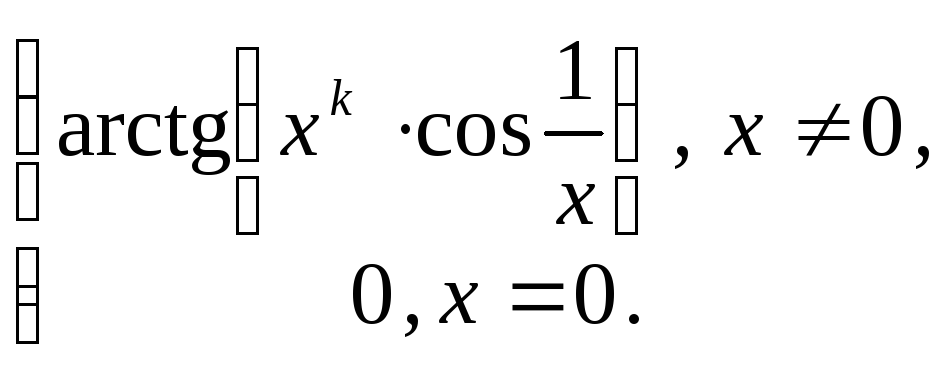 8.24
8.24
![]()
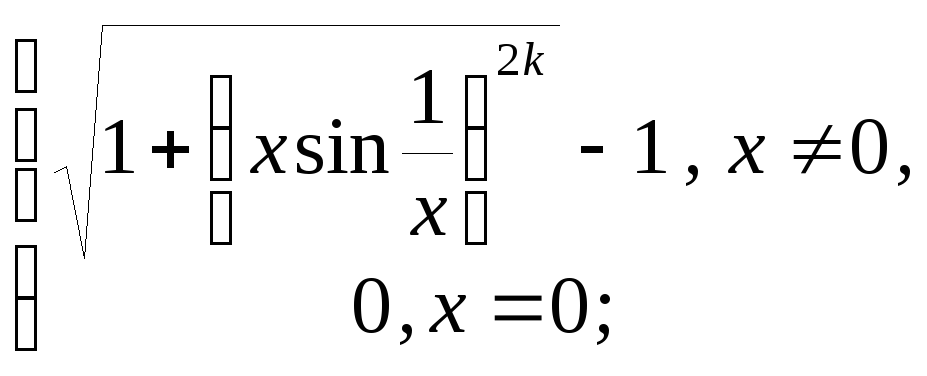
9. Найти производную:
9.1 ![]() . 9.2
. 9.2 ![]() .
.
9.3 ![]() . 9.4
. 9.4 ![]() .
.
9.5 ![]() . 9.6
. 9.6 ![]() .
.
9.7 ![]() . 9.8
. 9.8 ![]() .
.
9.9 ![]() . 9.10
. 9.10 ![]() .
.
9.11 ![]() . 9.12
. 9.12 ![]() .
.
9.13 ![]() . 9.14
. 9.14 ![]() .
.
9.15 ![]() . 9.16
. 9.16 ![]() .
.
9.17 ![]() . 9.18
. 9.18 ![]() .
.
9.19 ![]() . 9.20
. 9.20 ![]() .
.
9.21 ![]() . 9.22
. 9.22 ![]() .
.
9.23 ![]() . 9.24
. 9.24 ![]() .
.
10. Найти
![]() для функции, заданной параметрически
и неявно:
для функции, заданной параметрически
и неявно:
10.1 а)
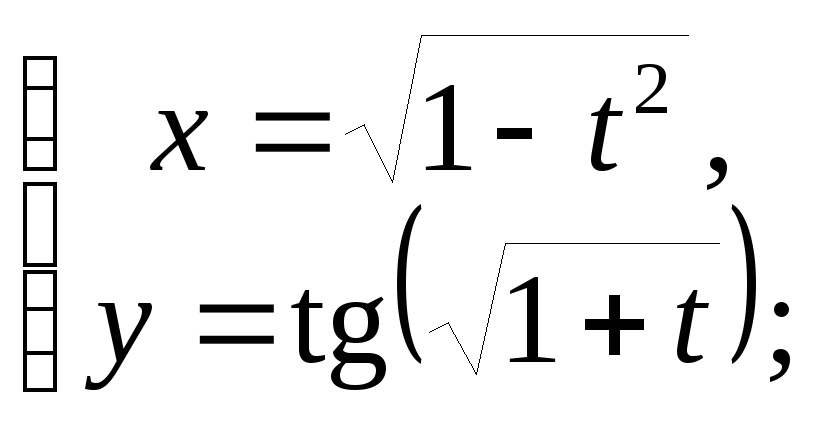 б)
б)
![]() .
.
10.2 а)
![]() б)
б)
![]() .
.
10.3 а)
![]() б)
б)
![]() .
.
10.4 а)
![]() б)
б)
![]() .
.
10.5 а)
![]() б)
б)
![]() .
.
10.6 а)
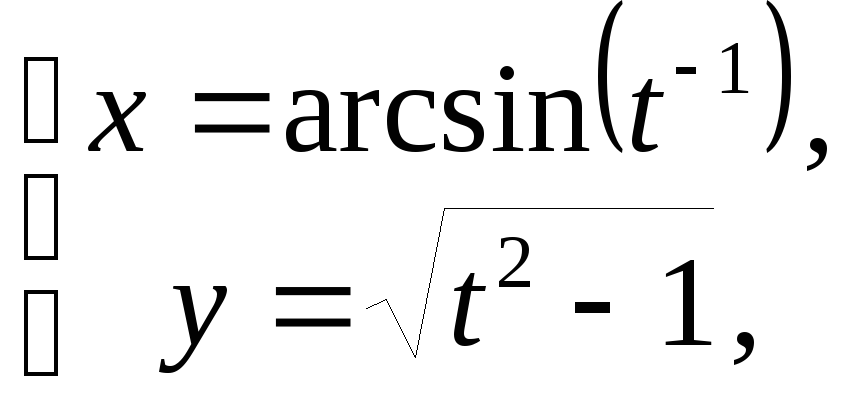 б)
б)
![]() .
.
10.7 а)
![]() б)
б)
![]() .
.
10.8 а)
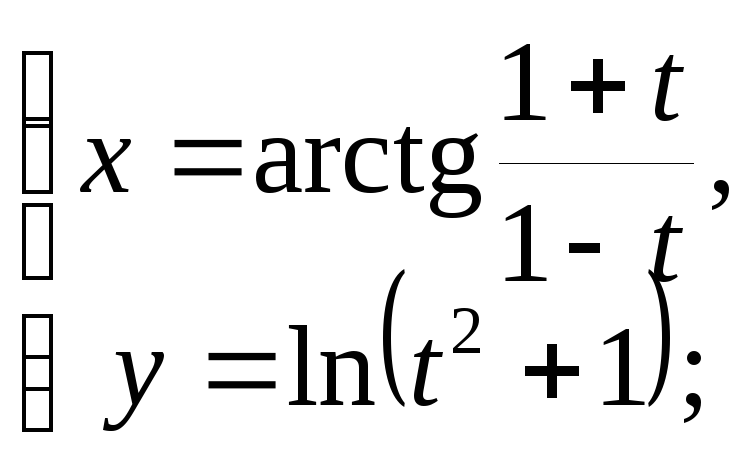 б)
б)
![]() .
.
10.9 а)
 б)
б)
![]() .
.
10.10 а)
 б)
б)
![]() .
.
10.11 а)
![]() б)
б)
![]() .
.
10.12 а)
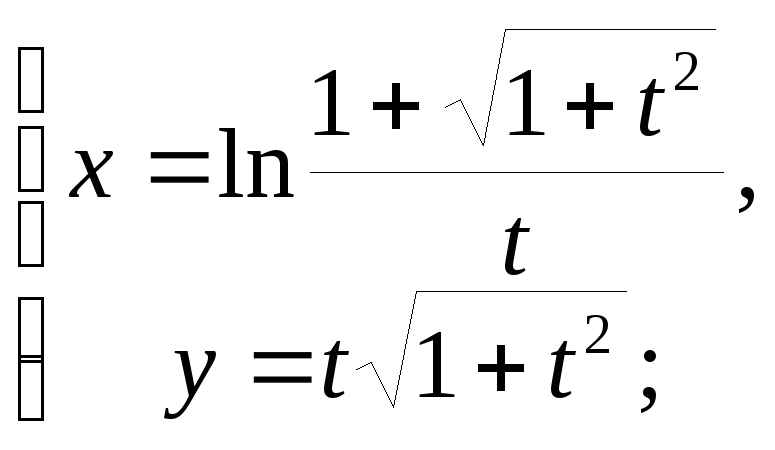 б)
б)
![]() .
.
10.13 а)
![]() б)
б)
![]() .
.
10.14 а)
![]() б)
б)
![]() .
.
10.15 а)
![]() б)
б)
![]()
![]() .
.
10.16 а)
![]() б)
б)
![]() .
.
