Задачи и размышления о множествах

1. Студенческая группа сформирована из выпускников лицеев (множествоA), специализированных классов (множество B) и общеобразовательных школ (множество С). Что означают множества и ? Верно ли соотношение

=?

Ответ. Нет. Почему?

2. Среди всевозможных треугольников выделите три множества и треугольников, для которых были бы справедливы утверждения:

а)

б)

в)

г) ;

д)

Ответ. Из утверждений а) – д) → А = В = С = Например: А – множество треугольников с суммой улов больше 180^о, В – треугольники, у которых одна сторона длиннее суммы двух других его сторон, С – треугольники, у которых длина одной стороны меньше, чем разность двух других его сторон. Таких треугольников не существует, и можно сказать, что такие множества пустые.

3. Дано множество

Какие множества можно образовать из его элементов?

Ответ: Множество положительных чисел , множество не положительных целых чисел , …

4. Сколько может быть подмножеств множества, содержащего n элементов?

Ответ: Их число равно . Почему? - это количество n разрядных двоичных чисел. Если i-ый элемент есть в подмножестве, то в i-ом разряде числа пишут 1, если i-ого элемента в нём нет, то – 0.

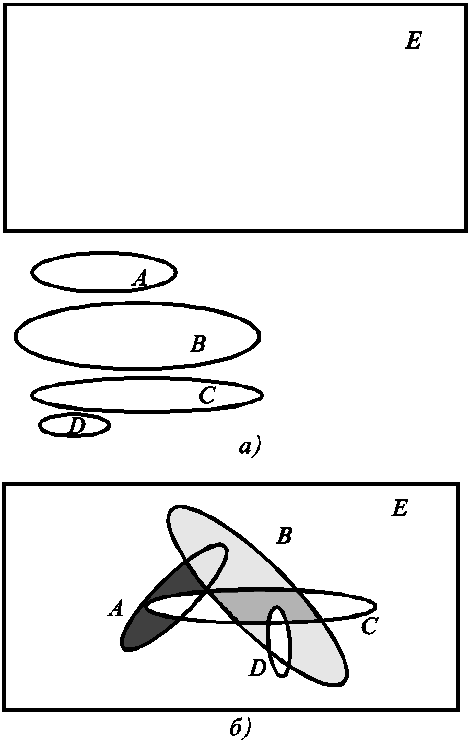
4. Даны множест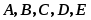ва (рис.7.10). Как будут выражаться через них одинаково заштрихованные множества?

Рис. 7.10 . Исходные множества и связь между ними.

6. В Мировом океане известно 19 глубоководных впадин, глубина которых превышает 7 километров, из них 16 находятся в Тихом и Индийском океанах, а 4 - в Индийском и Атлантическом. Сколько в каждом океане глубоководных впадин?

Решение. Пусть А - множество глубоководных впадин в Тихом и Индийском океанах, B - множество глубоководных впадин в Индийском и Атлантическом океанах. По условию число элементов в этих множествах . Известно также, что . Глубоководные впадины Индийского океана образуют множество . Для отыскания числа элементов этого множества используем формулу

согласно которой

Таким образом, в Индийском океане одна глубоководная впадина, а потому в Тихом океане их 15, а в Атлантическом - 3.

Отметим, что данную задачу можно было бы решить и традиционным алгебраическим методом. Если x, y и - число глубоководных впадин соответственно в Тихом, Индийском и Атлантическом океанах, то

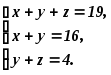
Решая эту систему, получим , что и является ответом задачи.

7. Можно ли обобщить формулу для нахождения числа элементов пересекающихся множеств на случай, когда этих множеств 3, 4,..., n?

Ответ: Да, можно. Например, для трёх множеств и из

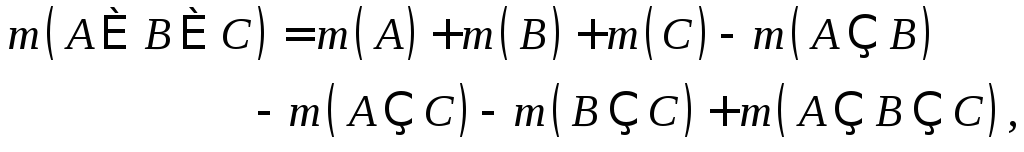
и формул задачи 6 для ,иимеем:

Используя для множеств , , D и эти равенства, получим:

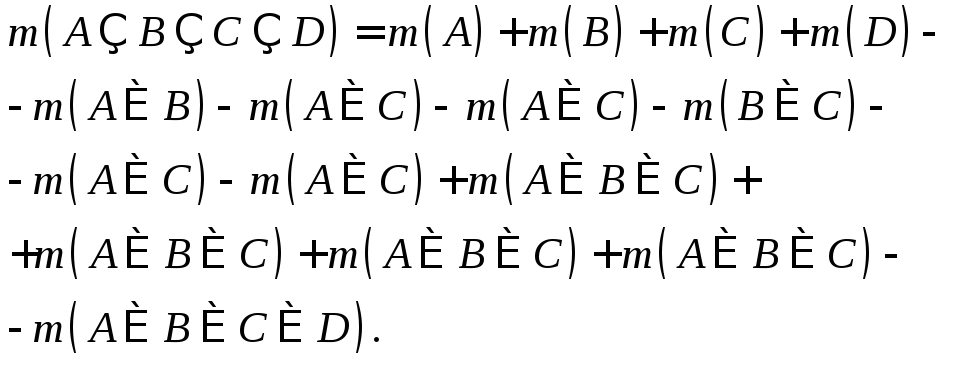
Здесь прослеживается закономерность и обобщение этой последовательности тождеств на n множеств очевидно.

8. Среди восьмидесяти участников математической олимпиады 60 человек любят шахматы, 50 - шашки, а 40 человек любят обе игры. Сколько участников олимпиады равнодушны к этим играм?

Решение. Пусть А – множество участников олимпиады, любящих шахматы, B – множество участников олимпиады, любящих шашки и множество С – множество участников олимпиады, которые равнодуш­ны к этим играм. По условию задачи = 60, = 50, обе игры любят = 40 олимпийцев, общее число участников математической олимпиады = 80, множестваине пересекаются, , и , где. То­гдаучастников равнодушны и к шахматам, и к шашкам.

9. В город Пермь прибыло 110 туристов. 80 из них решили посетить художественную галерею, 70 человек направились в Кунгурскую ледяную пещеру, 8 человек решили ограничиться только хождением по магазинам. Сколько человек посетили и художественную галерею, и Кунгурскую ледяную пещеру?

Решение. Пусть А – множество туристов, посетивших художественную галерею, , B – множество туристов, побывавших в Кунгурской ледяной пещере, ; множество E всех туристов считаем основным, универсальным, . Туристы, ходившие только по магазинам, образуют множество . Известно, что . По тождеству де Моргана

Тогда

Но

Применяя известную из задачи 6 формулу получим: